ARIMA-GARCH隨機收益鞅過程下冪型交換期權定價

鄭曉陽，仲崇雨

(哈爾濱工程大學理學院，黑龍江哈爾濱150001)

隨著期權市場的不斷發展，期權定價問題成為金融數學的核心問題之一.1973年，美國金融學家F.Black等提出了經典的Black-Scholes期權定價模型［1］，該模型在數學上的嚴密性有利于計算，但其股票價格遵循幾何Brown運動，且股票收益波動率為常數的假設與實際市場差別很大.大量的研究表明，股票收益的波動率是隨時間變化的，因此其實際應用性受到了學者們的廣泛質疑.在股票期權交易中，波動率是一個重要的因素，它是標的資產收益率的條件方差，是隨時間變化的.然而波動率又不能被直接觀測，這給眾多金融學者的研究帶來了一定的困難.但是波動率的一些特征往往能夠通過資產收益率序列觀察到.

1973年，D.E.P.Box等提出了自回歸滑動平均模型(auto-regressive moving average mode1，ARMA)建模方法，一般可得到較滿意的模型.但某些時候實際情況很復雜，很難看出運行規律從而得出序列不平穩的信息，這時可以不提取確定項，而對原序列進行差分(用原序列中的當前觀測減相鄰的后一個觀測)消除趨勢和周期，使之平穩，然后再擬合模型，此時的模型稱為自回歸求和移動平均模型(auto-regressive integrated moving average model， ARIMA).

1982年，Engle等提出了自回歸條件異方差模型(autoregressive conditional heteroskedastic model，ARCH)［2-5］.1986年，L.Bollerslev在ARCH模型的基礎上進一步提出了廣義自回歸條件異方差模型(generalized autoregressive conditional heteroskedastic model，GARCH)，它能夠反映出金融市場上資產收益率的“尖峰厚尾”現象和其波動的集群現象［4］.GARCH模型由于充分考慮到了波動率的具體特征，而不僅僅停留于理想的假定狀態，因而在對時間序列波動性的解釋和建模上具有較強的優勢，因此具有廣泛的理論和實用價值［6-12］.更重要的是，GARCH模型為預測Black-Scholes期權定價模型中的波動率提供了一種行之有效的方法.

本文就是在傳統的資產定價中加入漂移率和波動率的鞅表示算法，在經典的隨機過程ARIMA和GARCH過程基礎上聯合建立了一個反映股價非線性特點的隨機過程ARIMA-ARCH，利用測度變換確定資產價格，從而對奇異期權定價提高其精度.

1 金融時間信息集的確立

考慮股票價格金融時間集:

令(Ω，F，{Ft}t≥0，P)是一個過濾概率空間，其中(Ft)t≥0是一個單調不減 σ－代數信息流，假定F0={0，Ω}，令表示風險資產價格過程，簡記為S(t)或St，它是F適應的.S0表示一無風險證券價格過程，在t時刻有dS0=rdt，其中r為無風險利率.

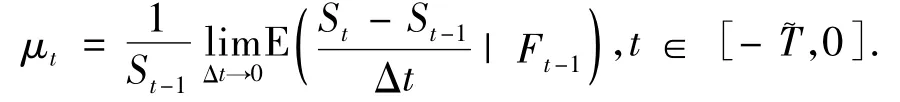
σt為t時刻的波動率:

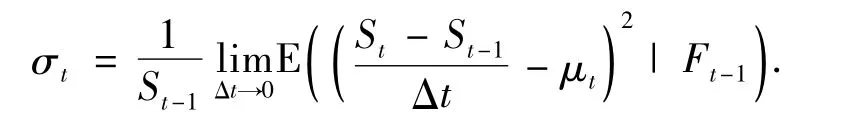
總收益率的自然對數被稱為連續復合收益率，或對數收益率:

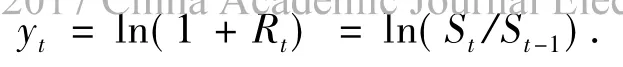
股票價格的波動率是不可觀測的，而且呈現出群集現象.因此，波動率研究的基本思想是:對數收益序列{yt}是前后不相關的或低階前后相關的，但不是獨立的.考慮給定t－1時刻已知的信息集Ft－1時，yt的條件均值和條件方差，即

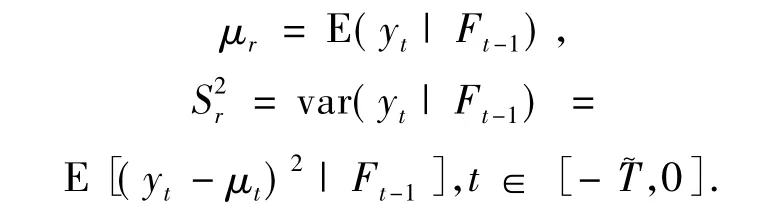
股票價格對數收益的ARIMA(m，n)－GARCH (p，q)鞅過程，即ARIMA－GARCH:

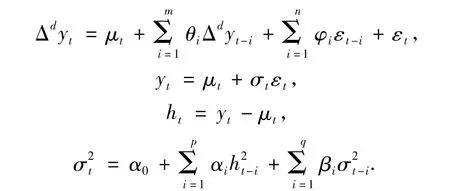
式中:d為差分階數;參數θi，i=1，2，…，m;參數φi，i=1，2，…，n;m≥0，n≥0;p≥0，q≥0;αi≥0，i=1，2，…，p;βi≥0，i=1，2，…，q.且 εt|Ft－1～i.i.d.

2 在ARIMA-GARCH鞅過程下股價的隨機微分方程

令(Ω，F，{Ft}t≥0，P)是一個過濾概率空間，定義市場上存在2個風險資產S1和S2，及一個無風險證券S0.

定理1 帶有紅利支付標的資產價格服從如下的隨機微分方程(stochastic differential equations，SDE):

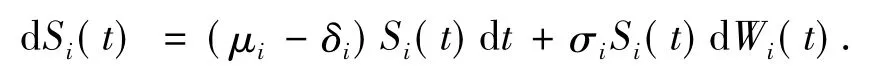
式中，t∈［0，T］，i=1，2.

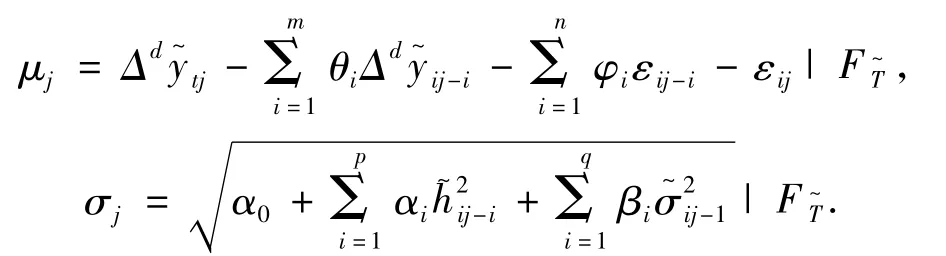
證明 在測度P下，令

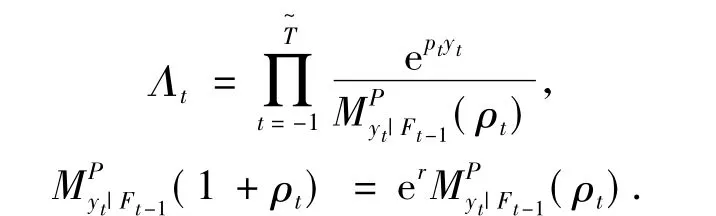
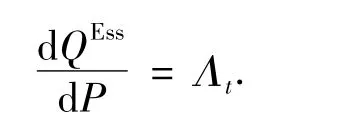
滿足Esscher測度變換，可知在測度QEss下:

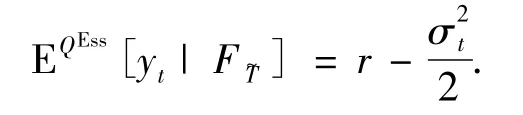
其中帶有紅利支付標的資產價格服從的隨機微分方程的解為

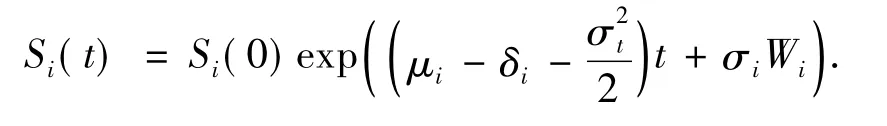
在測度P下

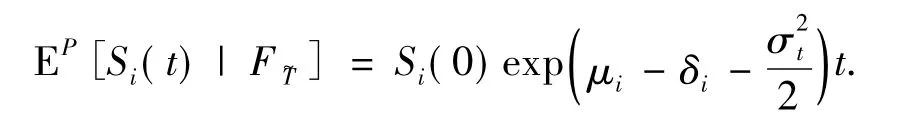
貼現后得到

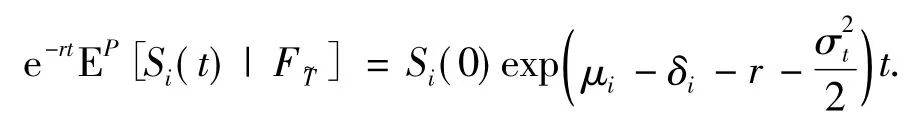
在測度QEss下貼現去紅利可以得到

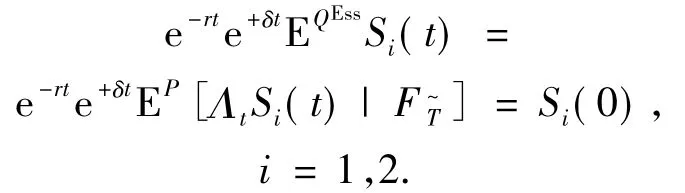
定理得證.

3 基于ARIMA-GARCH參數下由布朗基變換模型

由Wi(t)(i=1，2)是一個在測度P標準布朗運動，且dW1dW2=ρdt，由W1(t)、W2(t)變為B1(t)、B2(t2)得到

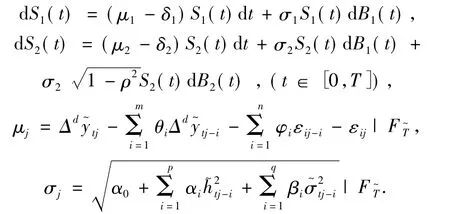
這里關于μj、σj中t∈［－，0］，j=1，2這里B1(t)和B2(t)在(Ω，F，{Ft}t≥0，P)上是相互獨立的布朗運動，在這樣的市場環境沒有套利機會當且僅當存在一個概率測度，使Si/S0為一鞅(i=1，2).由Girsanov定理可得

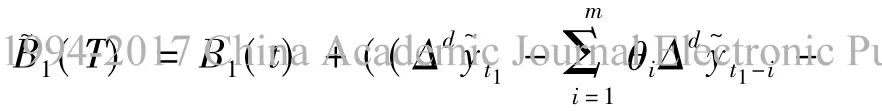
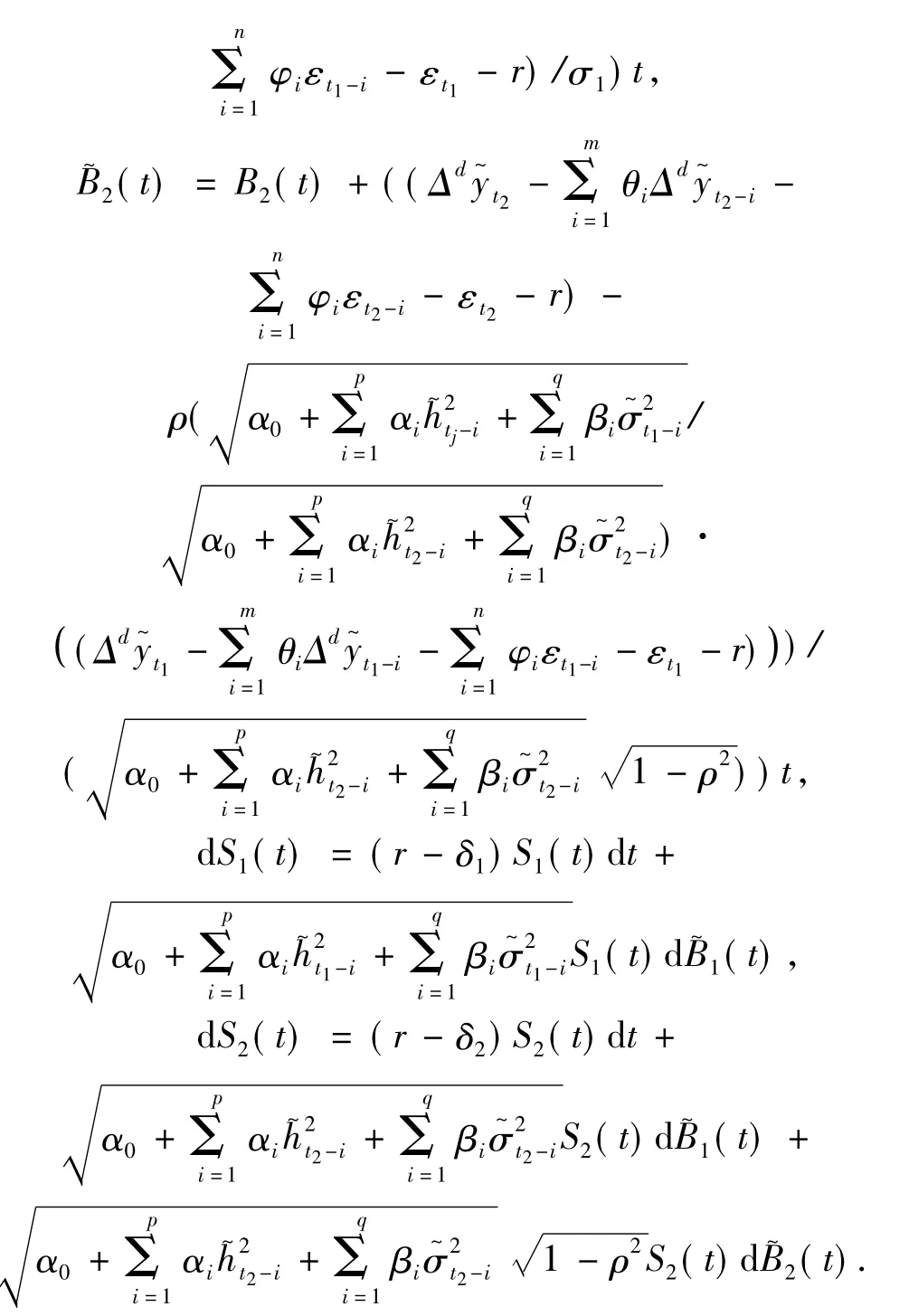
定理2 基于ARIMA-GARCH隨機收益鞅過程下具有紅利的線性冪型支付的交換期權定價:

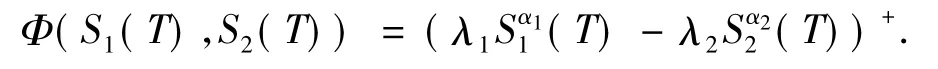
在t時刻的歐式看漲冪型交換期權ξ=(r，α1，α2，λ1，λ2，δ1，δ2，σ1，σ2)，在到期日T＞t有

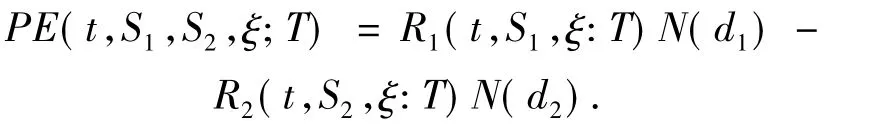
其中:

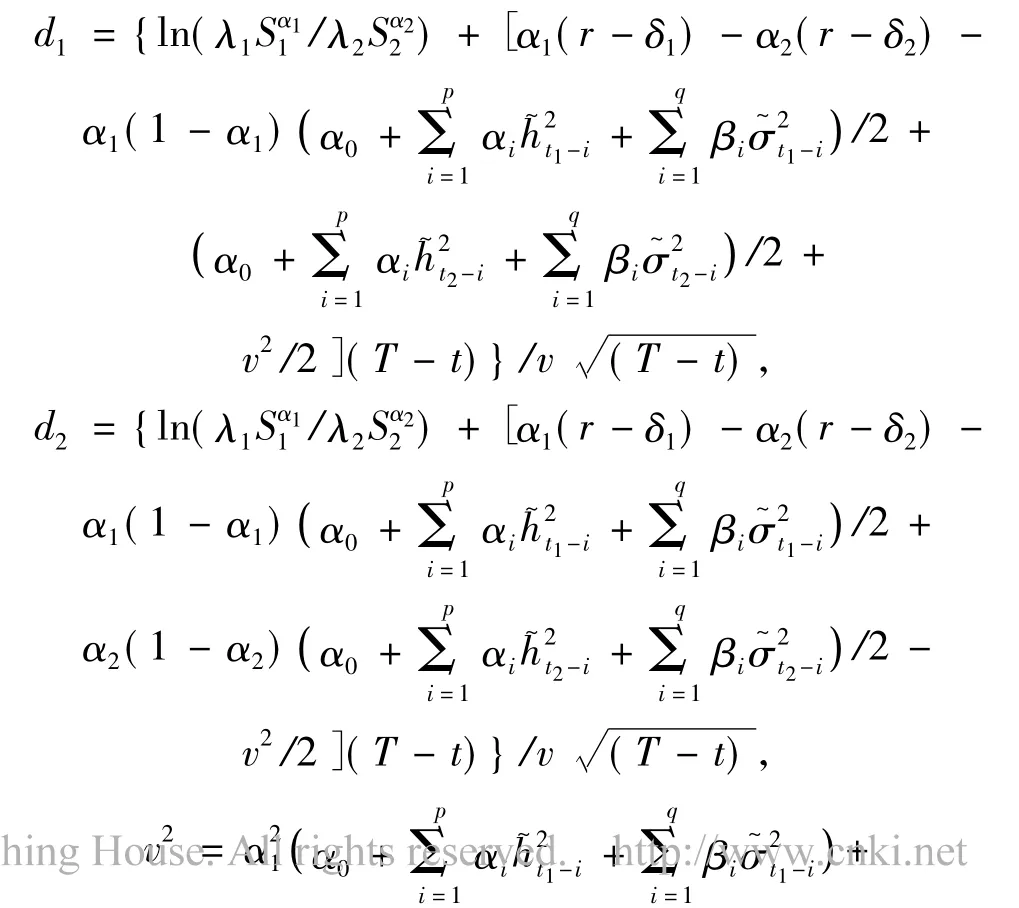
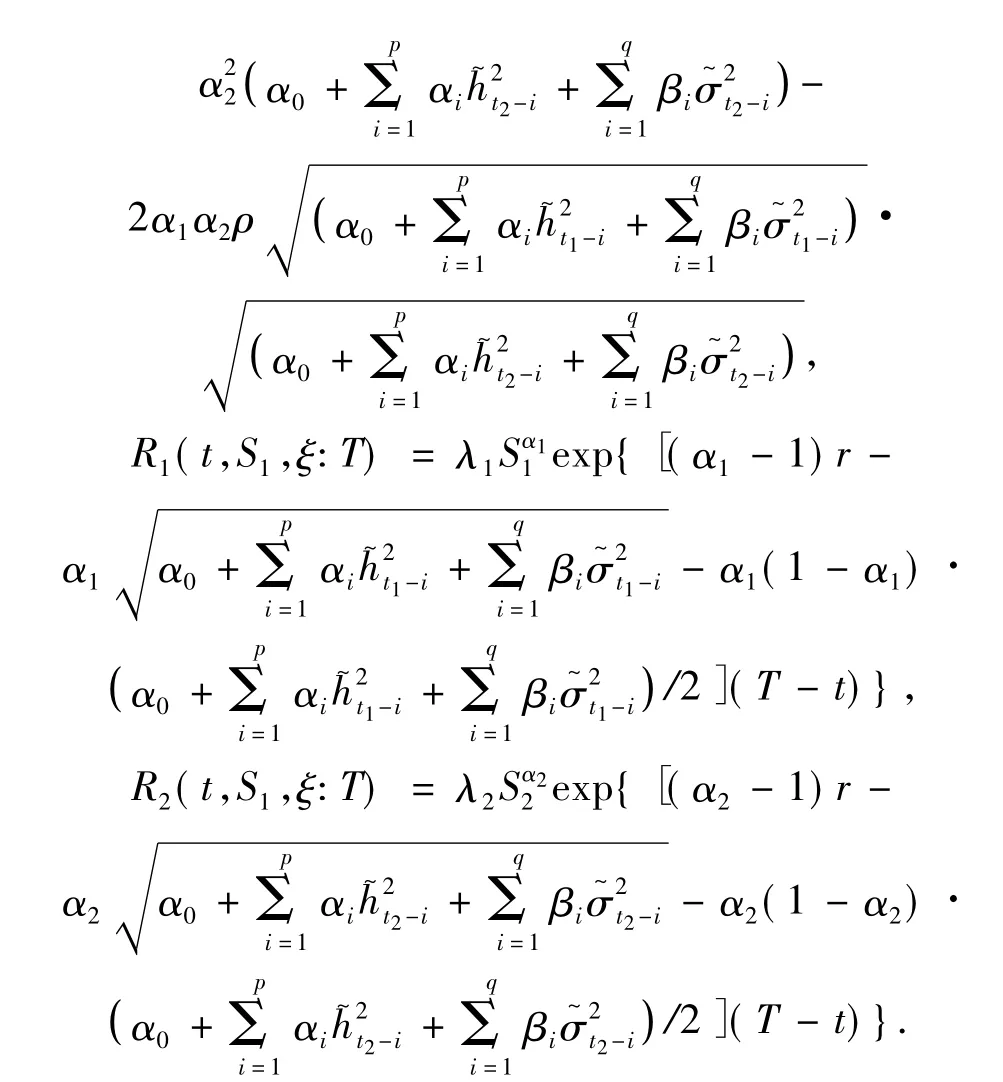
N(·)是一個正態分布函數.

證明

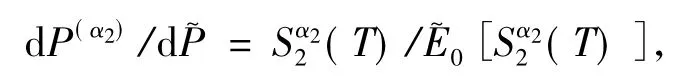
得到

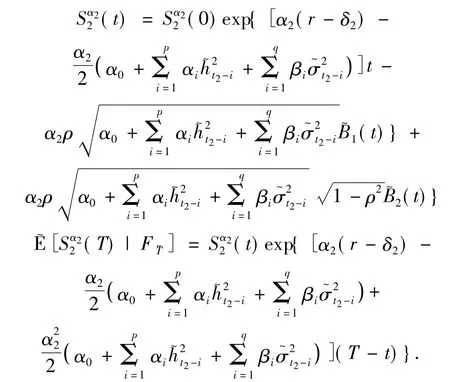
使得

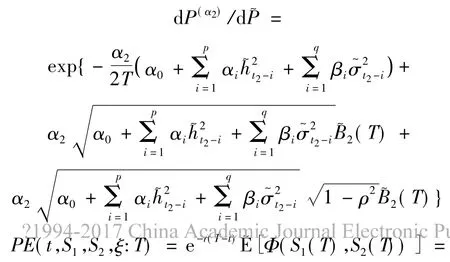
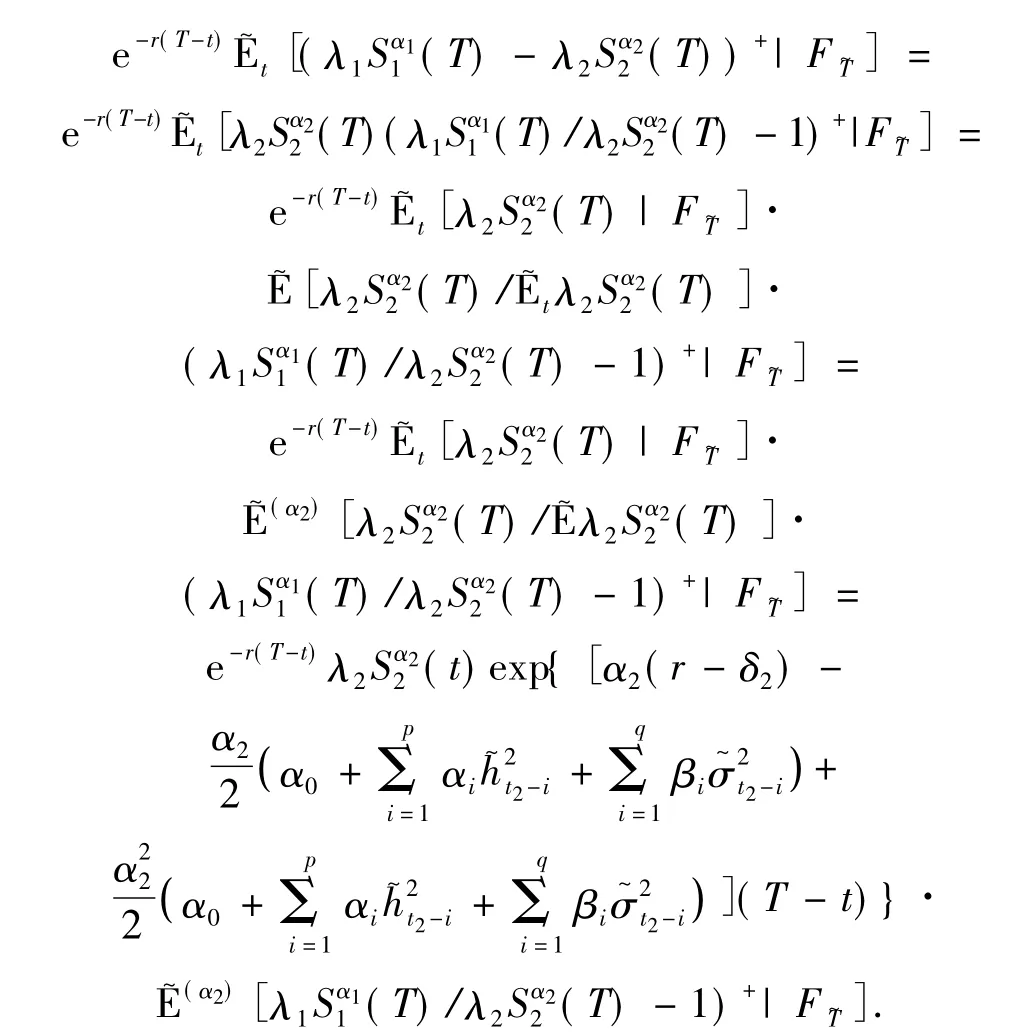
在測度P(α2)下有

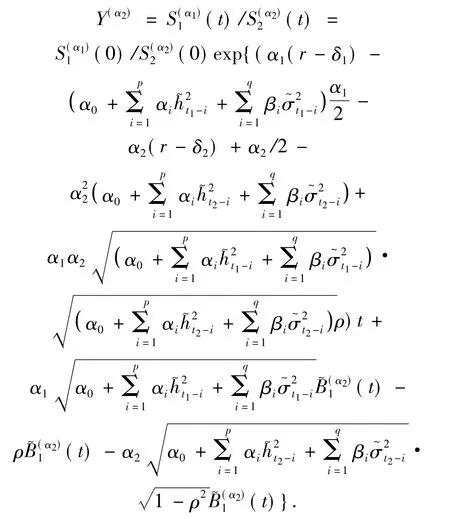
其中:

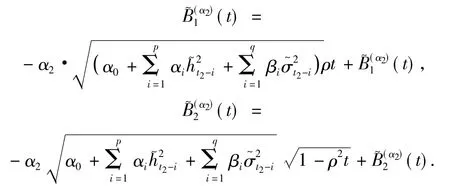
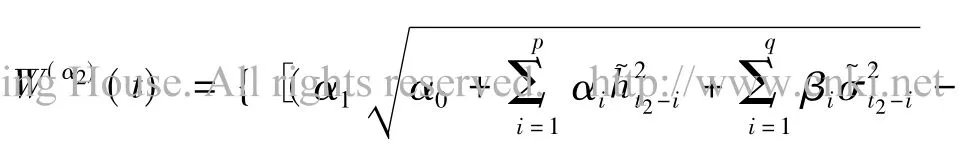
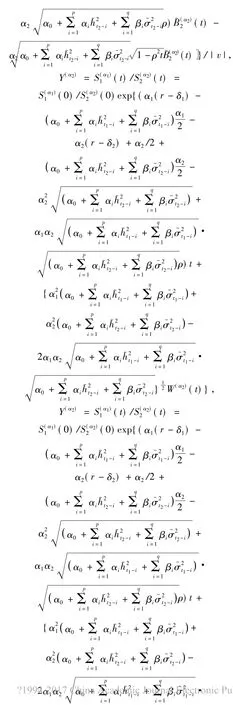
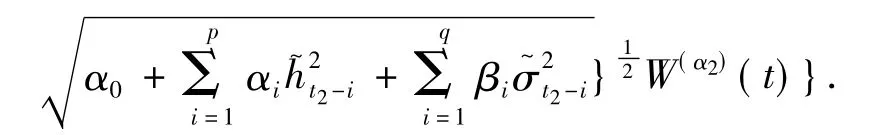
其中W(α2)(t)～N(0，t)，于是有

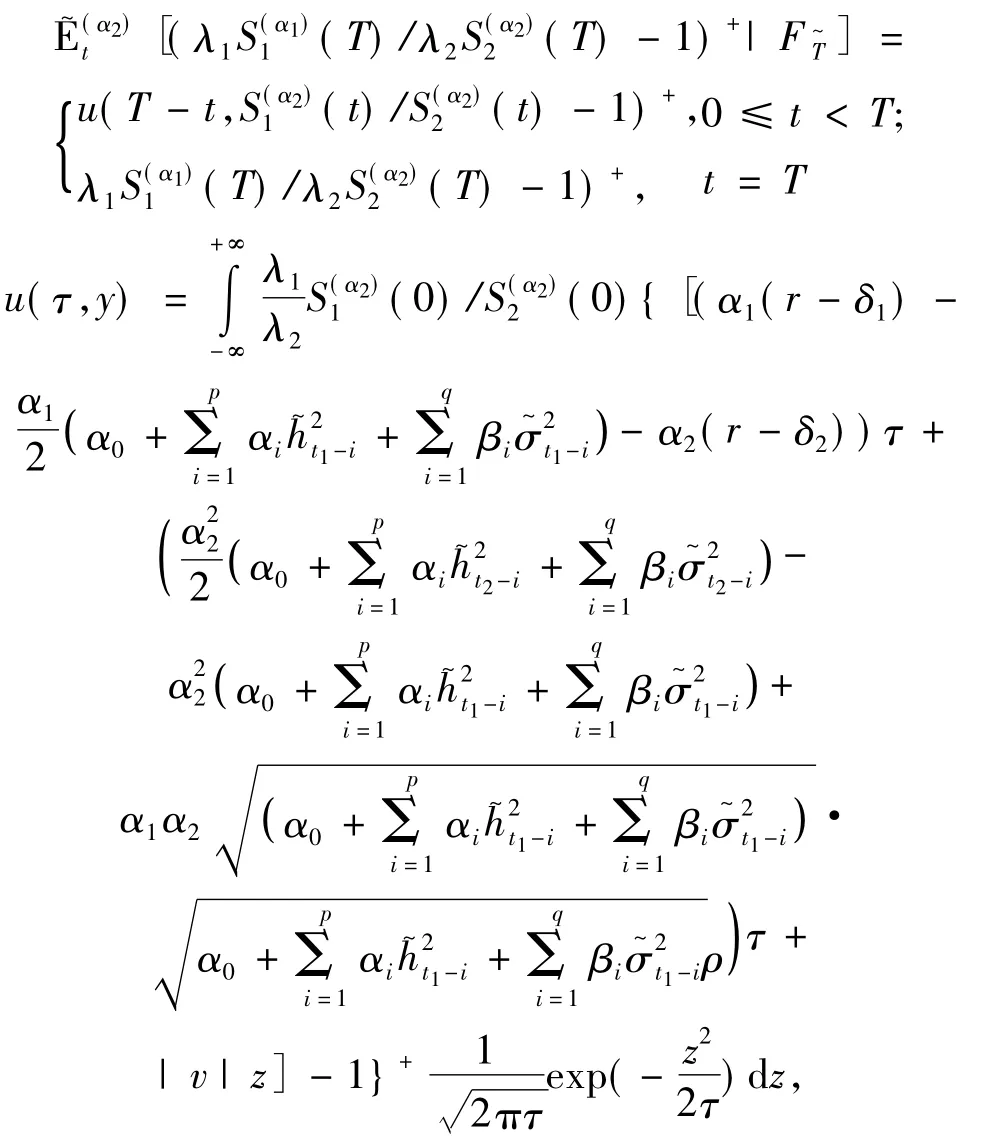
由于:

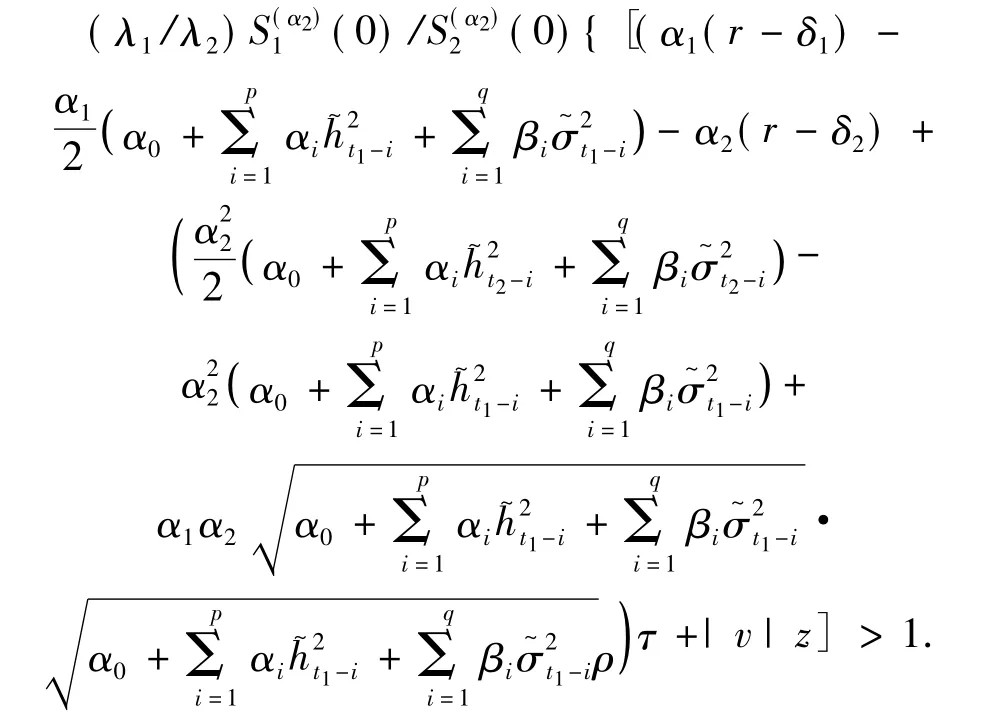
當且僅當

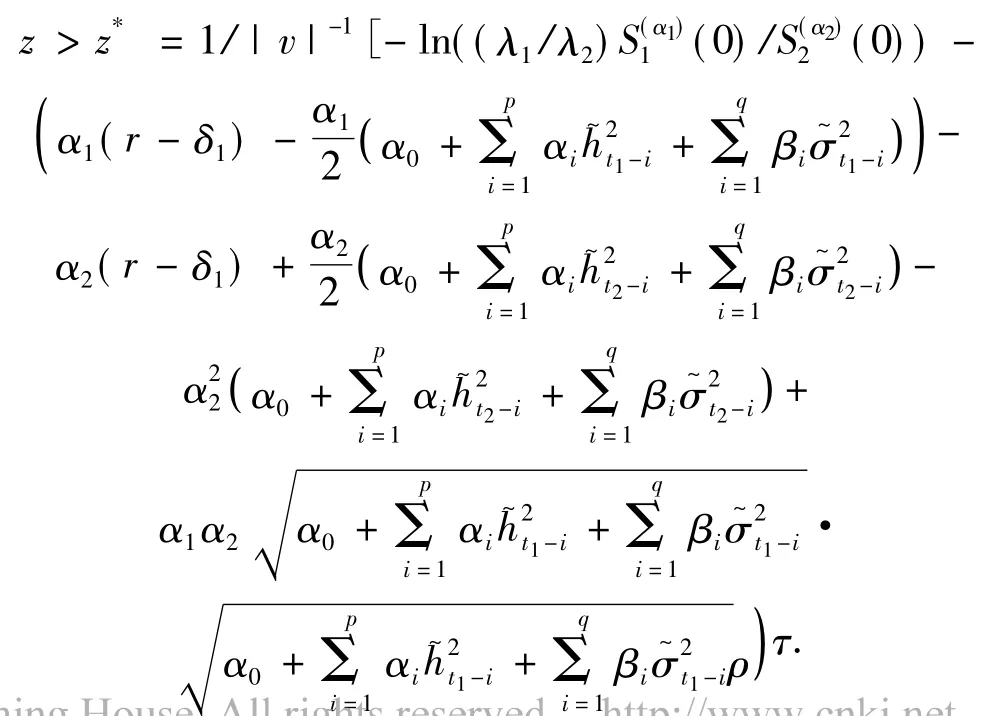
可以把原方程記為

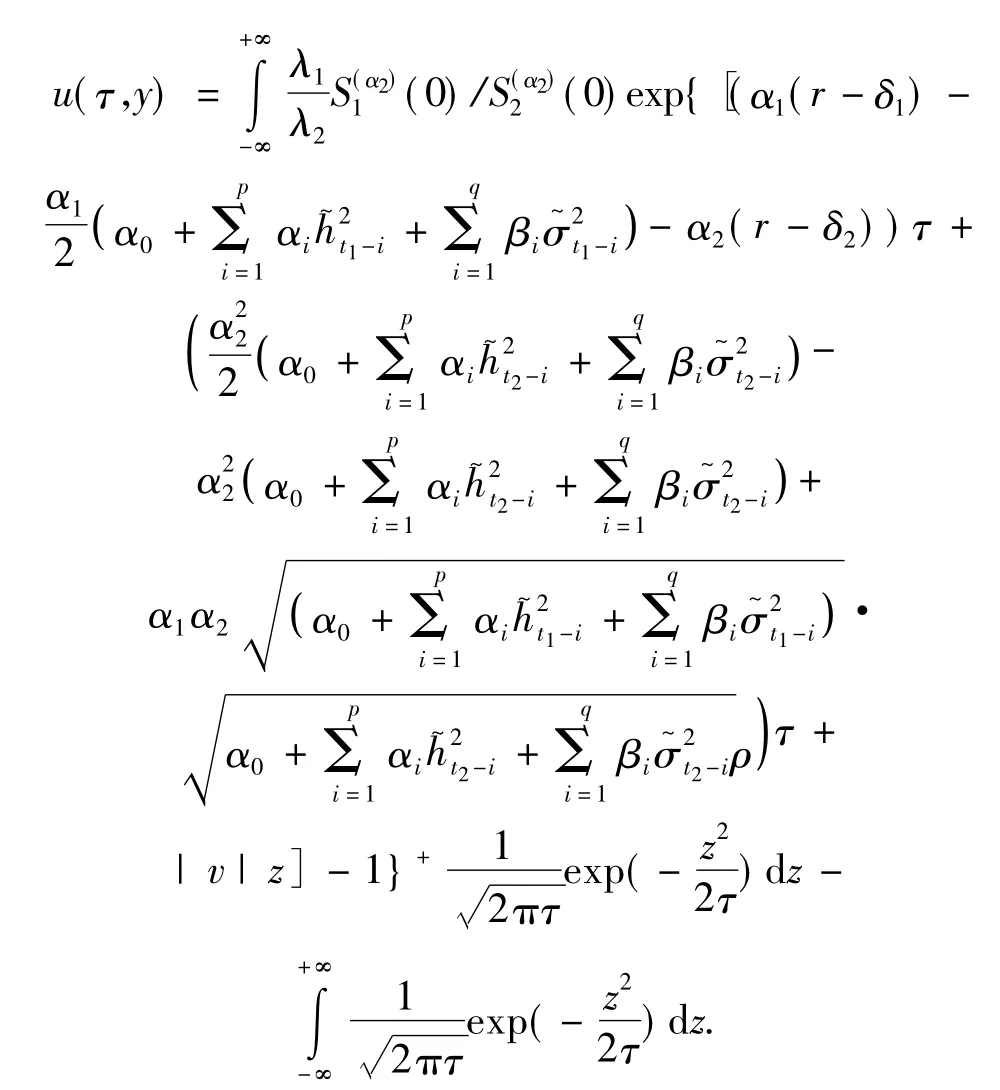
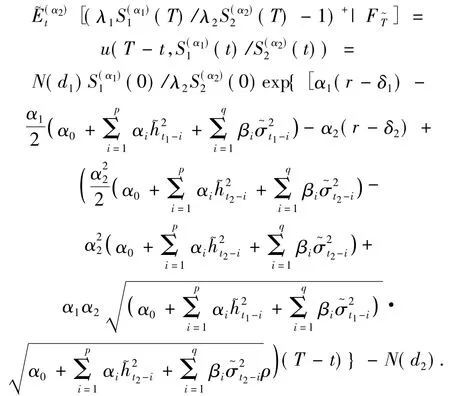
對于Ri(t，Si，ξ:T)，i=1，2，整理得到

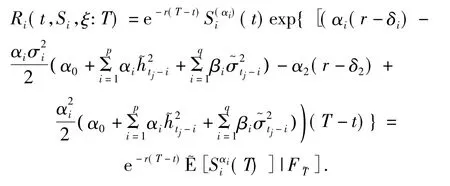
4 結論

本文通過在資產定價中加入漂移率和波動率的鞅表示算法，建立了一個反映股價非線性特點的隨機過程ARIMA-ARCH過程，利用測度變換確定資產價格，從而對奇異期權定價提高了其精度.

1)當資產S1(t)，S2(t)交換位置，則是看跌期權.當λ1=λ2=α1=α2=1，就變成標準的交換期權.

2)當λ1=1，α1∈R+，α2=0，λ2∈R+，就變成冪型看漲期權.

3)當λ1=1，α1=1，α2=0，λ2∈R+，執行價為λ2這就是熟悉的Black-Scholes模型.

［1］BLACK F，SCHOLES M.The pricing of options and corporate liabilities［J］.Journal of Political Economy，1973，81 (2):637-659.

［2］BOX G，JENKINS G，REINSEL G.Time series analysis: Forecasting and control［M］.3rd ed.New Jersey:Prentice Hall，2003:236-239.

［3］BOX G，PIERCE D.Distribution of residuan antocorrelations in autore-gressive-integrated moving average time series models［J］.Journal of the American Statistical Association，1970，29(3):1509-1526.

［4］BOLLERSLEY T.Generalized autoregressive conditional heteroskedasticity［J］.Journal of Econometrics，1986，31 (1):307-327.

［5］BARONE A，ENGLE G，MANCNI R.GARCH options in incomplete markets［C］//NCCR-FinRisk，Zurich:University of Zurich，2004:155.

［6］LLOYD B.Power exchange options［J］.Finance Research Letters，2005，18(2):97-106.

［7］ALEXANDDRA B，REG K.GARCH option pricing:a semiparametric approach［J］.Insurance:Mathematics and Economics，2008，43(2):69-84.

［8］ESSER A.General valuation principles for arbitrary payoffs and application to power options under stochastic volatility models［J］.Financial Markets and Portfolio Management，2003，17(1):351-372.

［9］ALISON E.A course in financial calculus［M］.Beijing: Post＆Telecom Press，2006:108-122.

［10］GERBER U.Actuarial bridges to dynamic hedging and option pricing［J］.Insurance，Mathematics and Economics，1996，18(1):183-218.

［11］ALATON P，DJEHICHE B，STILLBERGER D.On modeling and pricing weather derivatives［J］.Applied Mathematical Finance，2002，9(1):1-20.

［12］BATH E，SALTYTE J.The volatility of temperature and pricing of weather derivatives［J］.Quantiative Finance，2007，7(1):553-561.