嶺回歸分析方法在蘇里格氣田低滲透氣井壓裂效果分析中的應用
趙振東 (長城鉆探工程公司蘇里格氣田項目部,遼寧 盤錦124010)
1 單因素對氣井產量的影響
在對蘇里格氣田某區塊氣井壓后產量影響因素分析中發現,從單因素對壓后產量的影響曲線 (圖1)來看,滲透率、孔隙度、飽和度、儲層厚度等各種單因素對氣井壓后產量的影響幾乎毫無規律可尋。
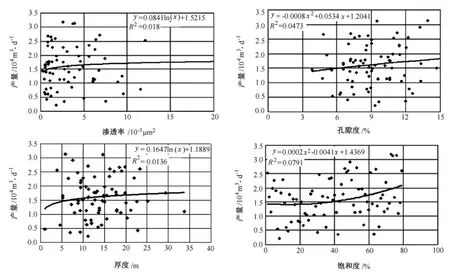
圖1 單因素對氣井產量的影響趨勢圖
參數間的相關性分析表明,有效厚度、滲透率 (孔隙度)、含氣飽和度、砂比、前置液量 (攜砂量、凈入地量、砂量、攜砂液排量、前置液排量)、返排率、停泵壓力之間是不相關的。有些參數之間是明顯相關的,例如滲透率與孔隙度、前置液量與攜砂液量和入地液量;而另外一些參數是相對獨立的,如停泵壓力與儲層參數、停泵壓力與液量或砂量等都是相對獨立的。用單因素分析的辦法沒有找到可適用的統計關系,或者說這種單因素模型根本不符合實際情況。
單因素模型不適用的主要原因[1]在于:①單因素分析方法中本身忽略了其他因素對產量的綜合影響。②單因素回歸曲線圖中相當部分樣本點與回歸值差值較大 (奇異點較多)。因此,必須對因素之間的相互作用進行研究。
影響氣井壓后產量的多種因素之間多重共線性是一個程度問題而不是有無的問題,為了消除多重共線性的問題,必須改進氣藏壓裂效果的評價方法。下面,筆者采用嶺回歸 (ridge regression)分析方法。
2 嶺回歸分析方法
嶺回歸分析是一種修正的最小二乘估計法[2],當自變量系統中存在多重相關性時,它可以提供一個比最小二乘法更為穩定的估計,并且回歸系數的標準差也比最小二乘估計的要小。在應用嶺回歸分析時,它的計算大多從標準化數據出發。
針對出現多重共線性時,標準化后的設計陣定義為:

式(1)為β的嶺回歸估計,由β的嶺估計求得的回歸方程便為嶺回歸。其中,k稱為嶺參數;假設X已經標準化,X-1X為自變量樣本相關陣。
嶺回歸首先要求取各個參數的嶺跡圖,即求出不同均方差參數k值下的嶺估計,然后根據嶺跡圖選取適當的k值,k值的選擇尤為重要,選擇k值的一般原則是:①各回歸系數的嶺估計基本穩定;②用最小二乘估計時沒有不合理的回歸系數;③回歸系數沒有不合乎經濟意義的絕對值;④殘差平方和增大不太多。
取k值趨向于平穩的值為適當k值,可以避免參數之間的相關性影響。參數的k值越早趨向于平穩參數越獨立。確定k值后,它將直接從減少誤差的均方根入手,修正參數前面的系數,求取合適的嶺回歸方程。
3 應 用
下面,筆者根據地質參數和施工參數,以產量為目標,根據各個參數的優化選取對具有強相關性的參數進行形式上的改變,得出優化的參數形式進行嶺回歸。
通過Matlab進行編程來算得不同k值下的回歸系數。經過多次的選取后最終選取了儲層有效厚度、滲透率、砂量、攜砂液量、地層儲集能力、前置液量、攜砂液排量和瞬時停泵壓力的參數數據進行回歸計算。氣層各參數的嶺跡圖如圖2所示。
由圖2可知,當嶺跡線趨于平穩后,所取得的橫軸方向上的k值就是符合最終回歸方程的k值。而越早趨于平穩的參數越獨立,反之,參數越和其他參數具有較強的相關性。當k取0.8時各回歸系數基本穩定了,在k=0.8時求得的標準回歸方程可以近似作為該區塊的產量預測分析模型。
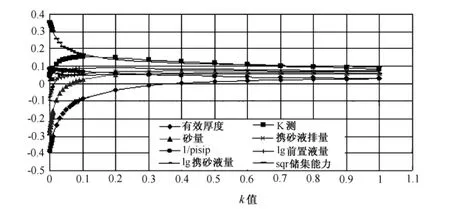
圖2 蘇里氣田某區塊嶺跡圖
4 結 論
通過對建立的產量預測分析模型分析可以得到以下幾點認識:
1)產量隨著儲層有效厚度增大而增大。儲層的有效厚度直接決定儲層儲量的大小,即儲層有效厚度越大可采的儲量也就越多。
2)產量隨著測井滲透率增大而增大。滲透率是決定著儲層物質流動性大小的,即滲透率越大參與流動的天然氣量也就越多,進而產量也就越大。
3)產量隨著加砂量增多而增大。加砂量越多,裂縫的寬度也就越大,進而也就增加了天然氣的流動能力。
4)產量隨著攜砂液量增大而增大。攜砂液量也決定著支撐裂縫長度的大小,即攜砂液量越大支撐裂縫長度越長。
5)產量隨著地層儲集能力增大而增大。儲集系數是綜合反映地層儲集能力大小的參數,一般地層儲集能力越大產量也就越大。
6)產量隨著停泵壓力增大而減小。
[1]孫東生,王紅才.影響水力壓裂效果的因素及人工神經網絡評價 [J].地質力學學報,2006(12):485.
[2]史世平.嶺回歸原理及其應用 [J].測繪科技,1995(3):31-35.

