弦支網殼結構中預應力拉索索力識別研究
馬德慧
含有預應力索的半剛性大跨度空間結構是一種非常有生命力的雜交鋼結構形式。單層球面網殼結構平面外剛度弱,通常由穩定性控制其承載能力,結構的材料強度得不到充分發揮,而索穹頂結構具有造價高、施工難度大等缺點,將二者結合起來形成的空間雜交鋼結構可以發揮兩種組成結構體系的優點,彌補各自不足,具有建筑造型適應性強、承載能力高、荷載作用下的結構變形小、結構穩定性強等優點。
近年來,索結構被廣泛應用于斜拉橋、懸索橋、拱橋、張弦梁屋架、平面索桁架、單層索網以及空間索網格等大跨和高聳結構中。索力直接控制索結構的內力分布和幾何線型,無論在結構施工過程中還是正常使用階段,都需要隨時準確了解索力的狀況,因此索力無疑是索結構健康狀態評估和監測的核心指標。
1 工程概況
山西體育中心游泳跳水館屋蓋結構為一整體鋼結構屋蓋,是由多重弦支網殼、空腹桁架與魚腹式桁架組成的綜合結構體系,其中,尤以多重弦支網殼部分的張拉施工和運營工況復雜,因此針對弦支網殼結構進行張拉施工監控,對成型后的游泳跳水館屋蓋結構進行運營階段的健康監測,采用振動法,對預應力鋼索索力進行監控。其中第[15]軸單榀主索結構如圖1所示,跨度為80m,矢高8.0m,垂度8.0m。鋼索分6個索段,下弦拉索為Φ5×163,各索段長度分別為左1段,8.944m;左2段,16.179m;左3段,16.080m。右側三段與左側對稱分布。拉索材料幾何參數見表 1。
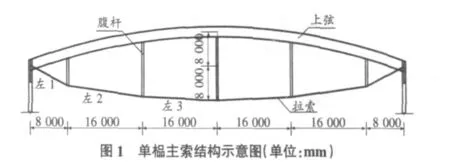

表1 鋼索幾何參數表
2 索力計算理論
在工程實際中,常用的索力測定方法主要有壓力表測定法、壓力傳感器測定法、扭力扳手測試法、振動法(頻率法)及磁通量法。前三種方法一般僅適用于正在張拉索的索力測定,后兩種方法可對施工完畢的拉索進行索力的復核。振動法可以在結構完工后再進行測試,測試簡便易行,容易檢查及維修,適合于長期監測。
振動法原理是首先通過振動測試,識別出索的自振頻率,由于索力與其振動頻率之間存在著特定的關系,索力可由頻率換算而間接得到。
本文以游泳跳水館多重弦支網殼結構索力測試為工程背景,運用頻率法基本理論,來測定結構下弦預應力鋼索索力值,確定使用過程中索力的大小和變化,使結構保持一個良好的受力和工作狀態。以下分別闡述了目前國內外學術界在振動法測索力方面具有代表性的三種計算公式。
1)兩端鉸支拉索索力計算。
根據弦的振動理論,將拉索理想化為張緊的弦,當其垂度的影響忽略不計時,其在無阻尼時的自由振動方程為[1]:

其中,y(x,t)為索上各點在各時刻時的豎向位移;EI為索的抗彎剛度;T為索的張力,假定其為常量,不隨時間和位置而變化; m為索的線密度,即單位長質量。對上述微分方程采用分離變量法,假定拉索兩端為鉸支邊界條件,可得到拉索的軸向拉力 T與振動頻率fn的關系為:

其中,n為拉索振動階數;fn為拉索第n階自振頻率;l為索長。該式稱為弦理論計算公式,目前廣泛應用于索力測試工程中。
2)兩端固定拉索索力計算。
當拉索邊界條件為兩端固定時,振動方程為一個超越方程,經過數值求解與擬合后,得出公式(3)[2]:

公式(3)可作為任意邊界條件下考慮彎曲剛度單索索力計算公式,需要做的是根據不同的邊界條件確定修正系數an,bn,以適應工程應用。上式的近似計算公式為:

3)由基頻進行索力計算。
當考慮拉索垂度和抗彎剛度等影響后,索的振動方程呈非線性,采用索振動的一階振型,用能量法推導出了分別考慮索垂度和抗彎剛度影響時索基頻與索力的關系,進而用曲線擬合方法建立了索力的實用計算公式[3]。當考慮抗彎剛度影響時,索力計算公式為:

3 拉索自振頻率測試
現場進行各索段自振頻率測試,在各索段中間布置加速度傳感器,對采集的加速度時程進行自譜分析,得到拉索左側三個索段的各階自振頻率。結果如表 2所示。
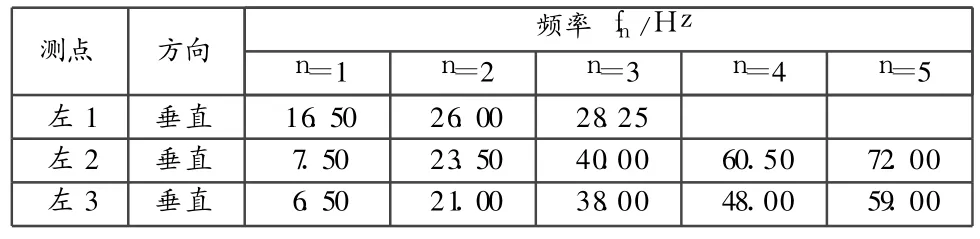
表2 [15]軸拉索左三跨頻率識別結果
4 拉索索力識別
根據弦理論公式、兩端固定公式及基頻計算索力公式,分別按式(2),式(4),式(5)計算索力,得到T1,T2,T3的數值,見表3。
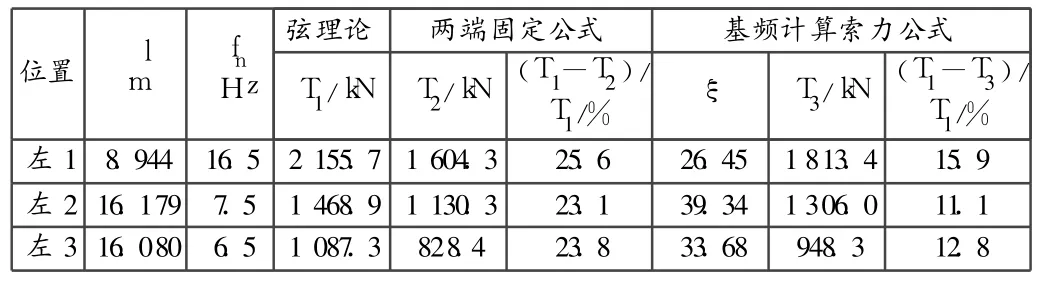
表3 三個索段索力識別結果
按弦理論來計算拉索索力,計算值偏大,主要由于該公式無法區分邊界條件、垂度等的影響,其適用范圍受到限制。按基頻計算索力公式計算的結果更接近真實值,根據文獻[3][4],該公式更具一般性且實現了簡支梁、固端梁與弦 3種模型間的連續過渡,得到的索力接近實際的受力狀態。
5 結語
1)弦理論是將拉索理想化為張緊的弦,但是由于忽略了拉索實際存在的垂度和抗彎剛度的影響,有時會帶來不可接受的誤差,誤差與索的長短有關,短索中受剛度影響較大,而當索長達到一定時,剛度的影響就很少了。2)本文以山西體育中心游泳館健康監測工程為背景,通過實測鋼索頻率值,對三種索力計算公式進行了比較與驗證,采用由基頻計算索力公式計算的結果與真實值較為接近,該公式可滿足計算精度要求。
[1] 向桂兵,李傳習.短吊索索力測試研究[J].山西建筑,2009,35(11):126-127.
[2] 秦 杰,高政國.預應力鋼結構拉索索力測試理論與技術[M].北京:中國建筑工業出版社,2010.
[3] 任偉新,陳 剛.由基頻計算拉索拉力的實用公式[J].土木工程學報,2005,38(11):26-31.
[4] Zui H,Shinke T,Namita Y.Practical formulas for estimation of cable tension by vibrationmethod[J].Journal of Structural Engineering,ASCE,1996,122(6):651-656.

