地震荷載作用下地下巖體洞室響應規律的研究

馬行東

(中國水電顧問集團成都勘測設計研究院，四川 成都 610072)

1 前 言

近年來世界范圍內發生的一系列大地震，使不少地下結構遭受破壞。隨著西部大開發戰略的實施，一大批大型水利水電工程已經或即將修建，而這些大型水利水電工程項目大部分處于強地震多發且高抗震設防地震烈度(地震動參數)地區。地震荷載作用下大型巖體洞室(隧道)安全將是工程建設中面臨的難點問題。

針對這一問題，國內外研究人員通過震后現場調查以及數值分析進行了一些卓有成效的研究工作。例如，文獻［1－4］根據地震后的現場調查分析了地下巖體工程的變形破壞模式、程度與覆蓋層厚度、巖石類型、支護類型、地震參數之間的關系;文獻［5－9］應用有限元、離散元等對一些影響因素進行了地震荷載下的洞室應力特性分析。本文嘗試采用FLAC初步分析埋深、洞室形狀、地應力、動力參數等對地震荷載作用下地下巖體洞室應力響應的影響規律，為工程設計提供參考。

2 計算模型及參數的選取

2.1 計算模型及邊界約束

在數值分析中，取100 m×40 m×150 m的區域為研究對象，洞室基本尺寸為10 m×40 m×10 m。計算模型、斷面形狀及數值分析中的監測單元位置見圖1。為減少動荷載作用下邊界反射波的影響，采用粘滯邊界［10］，約束邊界見圖1，局部阻尼系數取為0.125。

圖1 計算區域及邊界條件設置

2.2 巖石力學模型和參數

在數值模擬中，采用理想彈塑性模型，屈服準則采用Mohr－Coulomb強度準則，屈服函數如下［10］:

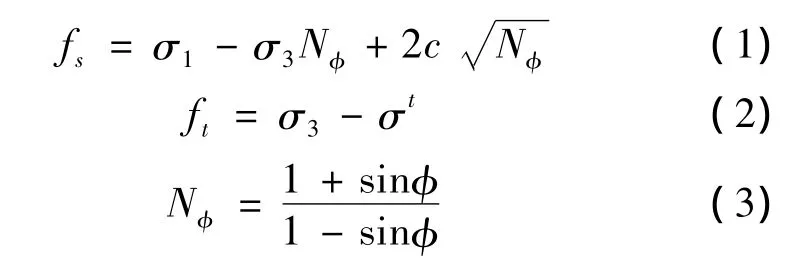
式中 σ1、σ3——分別為最大、最小主應力;

φ——摩擦角;

c——粘聚力;

σt——巖石抗拉強度。

當巖體內某一點應力滿足fs＜0時，發生剪切破壞;當滿足fs＞0時，發生拉伸破壞。

模型巖石介質為凝灰巖，其物理力學指標見表1［11］。

表1 巖石物理力學指標

2.3 荷載、洞型、埋深、地應力的確定

模擬的地震波為施加在模型底面的正弦剪切應力波，其速度時程為:v=λsin()。由于在粘滯邊界動態中，速度與加速度不能直接作用在模型邊界，而要轉換成力作用在模型上［10］:

為分析不同斷面洞室形狀下的位移響應，在數值分析中，取矩形、馬蹄形和圓形三種斷面洞室。馬蹄形斷面上部尺寸為半徑5m的半圓，下部為5m×10m的矩形;矩形斷面尺寸為10m×10m;圓形斷面的半徑為5m。三種模型取相同特殊監測單元。根據實際工程中洞室的可能埋深情況，數值分析中，埋深分別取為100m、200m、300m、500m、1000m。

實際分析中，取隧道軸向與最大主應力方向一致。垂直應力可近似表示為巖體自重(σV=λh)，最大水平主應力取為σh=λσv，側壓系數λ取值范圍為0.5、2、3、4，最小水平主應力取最大水平主應力的一半。

分析中，考慮地震烈度為Ⅴ、Ⅵ、Ⅶ、Ⅷ，各級烈度對應的參考速度指標分別為0.031m/s、0.062 m/s、0.13m/s、0.25m/s［12］。地震波的頻率范圍取0.5Hz、1Hz、2Hz、4Hz、10Hz、20Hz，地震持時取為1s、2s、4s、10s、20s［12］。

3 計算結果及分析

3.1 埋深、地應力的影響

圖2為地震引起的不同地應力、不同埋深情況下矩形、馬蹄形和圓形三種洞型拱頂、拱底的最小主應力變化曲線。由圖可見，在自重地應力為主(側壓系數λ＜1)的情況下，洞室拱頂、拱底受拉，此狀況洞室易發生張性破壞。在構造地應力為主(λ＞1)的情況下，洞室拱頂、拱底受壓，洞室相對穩定，但在地震荷載作用下洞室可能會發生剪切破壞。相對拱底、拱頂而言，地震引起的側墻應力則相對靜態側墻應力呈減弱變化，甚至向負向發展。另外，模擬還發現地震引起的洞室應力響應隨埋深、地應力的增加而減小，且地應力對洞室應力的影響程度大于埋深的影響。同時還發現，在側壓系數λ＜1下，當埋深超過300m后應力變化較小;而對于側壓系數λ＞1情況，埋深超過500m后應力變化較小。因此存在應力變化臨界值，且有隨側壓系數的增加應力變化臨界值由500m埋深減小到300m。

圖3為地震引起的拱頂、拱底最大主應力曲線。可以看出，在自重地應力為主(側壓系數λ＜1)的情況下的最大主應力小于構造地應力為主(側壓系數λ＞1)的情況。如前對σ3分析，側壓系數小于1，洞室容易發生張性破壞，因此λ＜1下的洞室破壞大于λ＞1的情況。另外，洞室應力值隨埋深、地應力的增加而減小，隨側壓系數的增加應力變化臨界值由500m埋深減小到300m。

3.2 洞型的影響

圖4、5是地震荷載引起的三種洞型的主應力圖。可以看出，不同斷面形狀的洞型拱頂和拱底的應力響應有一定區別，圓形洞室應力響應最小，矩形洞室應力響應最大。隨埋深的增加，應力響應減小，當埋深超過300m后，洞型對應力的影響變化程度不大。同時可以看出，在不同側壓系數情況下，圓形洞室的應力響應較矩形和馬蹄形的小。另外，地震荷載下，通常三種洞室的應力常集中于拱頂、拱底和兩幫，兩幫應力相對減小。

3.3 振幅的影響

圖6、7為振幅引起的矩形洞室拱頂、拱底的主應力曲線。可以看出，不同埋深、不同地應力下的應力隨振幅的增加而增加，但應力的增加幅值程度較小，沒有像應變隨振幅的增大而增加并伴隨有突變。另外，地震引起的應力隨埋深、地應力的增加而減小。同時，淺埋洞室、側壓系數λ＜1情況下的洞室應力值較大。

3.4 頻率的影響

圖8、9為矩形洞室拱底和拱頂的應力隨地震波頻率的變化規律。可以看出，淺埋情況下(埋深＜300m)，低頻(f＜2Hz)地震波導致的洞室應力幅值高于高頻(4～20Hz)地震波，但洞室應力幅值隨地震波頻率的增加變化幅度不大。隨著埋深的增加，不同頻率地震波導致的洞室位移幅值有減小趨勢，當埋深超過300m之后，洞室位移隨地震波頻率的增加變化較小。隨側壓系數的增加，不同頻率地震波導致的洞室位移幅值有明顯減小的趨勢，當側壓系數達到4之后，洞室位移隨地震波頻率的增加變化較小。

圖2 洞室最小主應力與埋深關系(不同地應力)

3.5 持續時間的影響

圖10、11、12為持續時間引起的馬蹄形洞室拱頂、拱底的主應力曲線。可以看出，不同埋深、不同地應力下的地震引起的應力隨持續時間的增加變化不大，拱頂應力有輕微的增加、拱底應力有輕微減小。另外，側壓系數λ＜1下，拱頂、拱底常發生張性破壞;而側壓系數λ＞1下洞室易發生剪切破壞。同時地震引起的應力都隨埋深、地應力的增加而減小，在埋深超過500m、側壓系數λ＞4的情況下洞室穩定性較好。因此，持續時間對洞室的應力影響不大，但長時間的應力狀態可以造成洞室的疲勞破壞。

3.6 地震荷載下洞室周邊應力分布

圖13、14為三種洞室地震荷載下的應力分布圖。對地震荷載下的不同埋深、不同地應力下的洞室主應力分析，對于淺埋洞室、以自重地應力為主的情況下的洞室應力拱頂、拱底易發生張拉破壞，而側墻由于靜態下受壓，故在動態下破壞沒拱底、拱頂明顯。此狀況常造成拱頂的塌落、拱頂的縱向開裂、人行道或拱底的拱起和開裂，隨埋深的增加還伴隨剪切破壞。而對于深埋洞室、以構造地應力為主的情況下的洞室則是側墻、拱底受拉，側墻、拱底易發生張性破壞，而拱頂相對來說則穩定一點。此狀況會造成側墻的張性開裂、側墻開口處的張性開裂、側墻向洞內的變形以及人行道或拱底的拱起和開裂。

圖3 洞室最大主應力與埋深關系(不同地應力)

圖4 不同埋深下洞室應力隨斷面變化情況(λ=2)

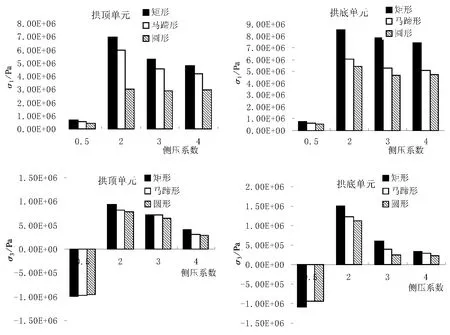
圖5 不同地應力情況下洞室位移隨斷面變化情況(埋深200m)

圖6 洞室主應力與振幅關系(不同地應力，埋深200m)

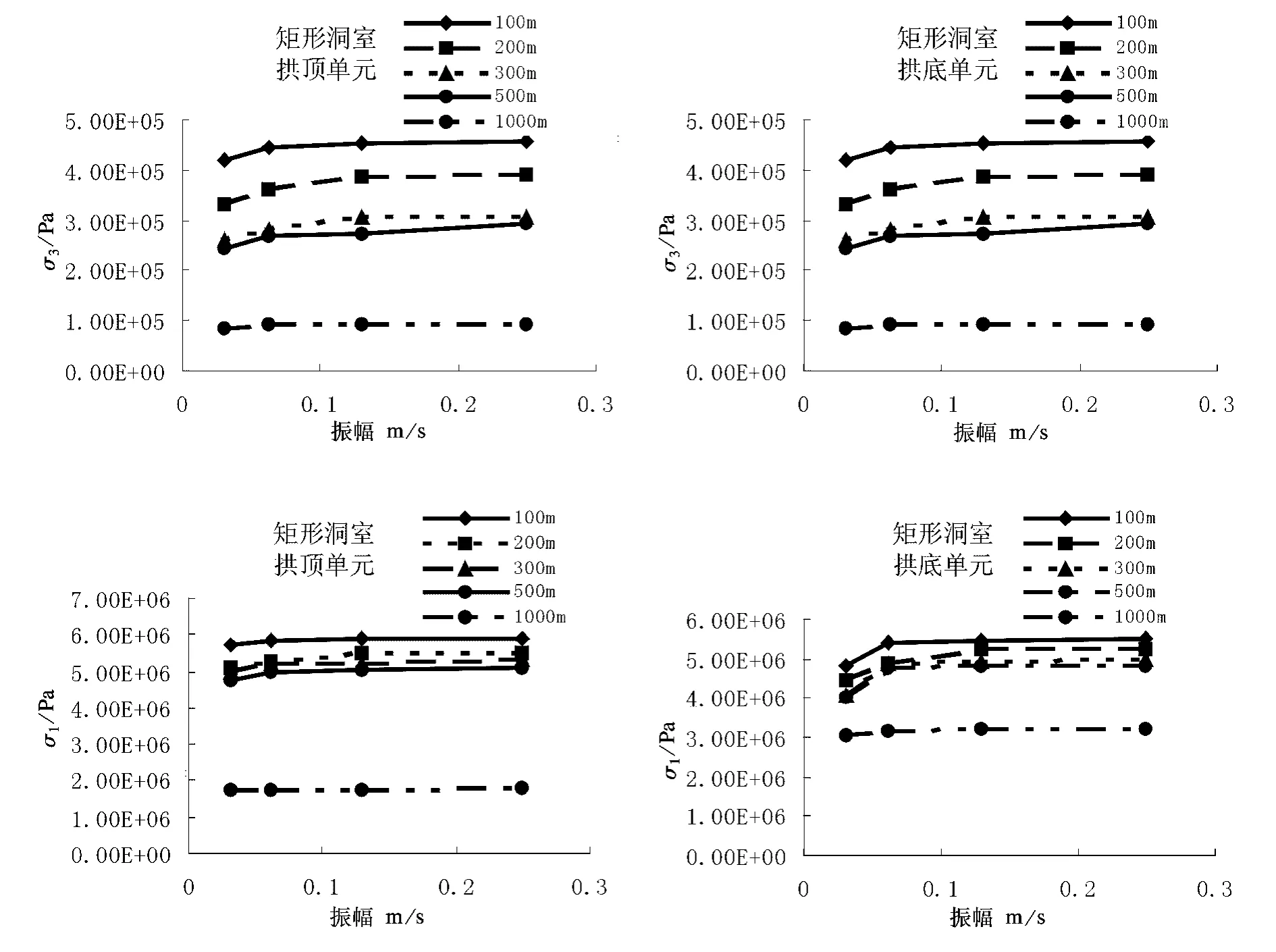
圖7 洞室主應力與振幅關系(λ=2，不同埋深)

圖8 洞室最大主應力與頻率的關系(埋深200m)

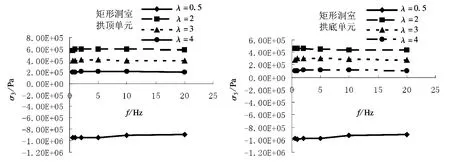
圖9 洞室最小主應力與頻率的關系(埋深=200m)

圖10 洞室最小主應力與持續時間的關系(埋深200m)

圖11 洞室最大主應力與持續時間的關系(埋深200m)

圖12 洞室最大主應力與持續時間的關系(λ=2)

圖13 淺埋、自重地應力為主下的洞室應力分布

4 結論與建議

本文利用FLAC3D分析了地震荷載作用下埋深、洞室形狀、地應力、動力參數等對巖體洞室應力特征的影響規律，研究結果表明:

圖14 深埋、構造地應力為主下的洞室應力分布

(1)地震荷載下，在自重地應力為主(λ＜1)的情況下，洞室拱頂、拱底常發生張性破壞，而在構造地應力為主(λ＞1)的情況下，拱底、側墻則易發生張性破壞。構造地應力為主(λ＞1)情況下的剪切破壞大于自重地應力為主(λ＜1)的情況，而張性破壞則小于前者。

(2)洞室應力響應隨埋深及地應力的增加而減小，隨側壓系數的增加應力變化臨界值由500m埋深減小到300m。

(3)洞室斷面形狀對洞室位移響應有一定影響。在數值分析中確定的地震荷載作用下以及地應力和埋深狀況下，圓形斷面洞室拱頂和拱底位移較矩形和馬蹄形的小。

(4)在地震荷載作用下，洞室位移幅值隨振幅、持續時間的增大而增大，變化幅度隨埋深和側壓系數的增加而減小。隨著頻率的增加，洞室位移幅值隨地震波頻率的增加有明顯的減小趨勢，變化幅度隨埋深和側壓系數的增加而減小。

［1］C F Lee.Performance of Underground Coal M ines During the 1976 Tangshan Earthquake［J］.Tunnelling and Underground Space Technology，1987(2):199 －202.

［2］鄭永來，楊林德.地下結構震害與抗震對策［J］.工程抗震，1999，12(4).

［3］Wang WL et al.Assessment of damage inmountain tunnels due to the Taiwan Chi－ Chi Earthquake［J］.Tunnelling and Underground Space Technology，2001，16:133 －150.

［4］于翔.地鐵建設中應充分考慮抗地震作用—阪神地震破壞的啟示［J］.隧道/地下工程，2000(4).

［5］韋敏才.地下結構的動力特性及地震反應分析［J］.昆明理工大學學報，1996.621(3).

［6］胡曉燕，周健，胡曉虎.地震引起的豎向壓應力對地鐵隧道的影響［J］.工程抗震，2000(2).

［7］金峰，賈偉偉，王光綸.離散元邊界元動力耦合模型在地下結構動力分析中的應用［J］.水利學報，2001(2).

［8］高峰，李祖德.隧道三維地震反應分析若干問題的研究［J］.巖土工程學報，1998，20(4).

［9］周德培.強震區隧道洞口段的動力特性研究［J］.地震工程與工程振動，1998.3(1).

［10］FLAC3D(Fast Lagrangian Analysis3 Dimensions)user′smanual，Version 2.0［M］.Itasca Consulting Group，Inc.，USA，1995.

［11］夏祥，李俊如.爆破荷載作用下巖體振動特征的數值模擬［J］.巖土力學，2008(11).

［12］胡聿賢.地震工程學［M］.北京:地震出版社，1988.