GRNN在邊坡穩(wěn)定預(yù)測(cè)分析中的應(yīng)用

狄圣杰,李曉敏,魏 檣

(1.河海大學(xué)巖土力學(xué)與堤壩工程教育部重點(diǎn)實(shí)驗(yàn)室,江蘇 南京 210098;2.鄭州科技學(xué)院土木與建筑工程系,河南 鄭州 450000;3.中國(guó)水電顧問(wèn)集團(tuán)昆明勘測(cè)設(shè)計(jì)研究院,云南 昆明 650051)

巖土體具有復(fù)雜的結(jié)構(gòu)和機(jī)理,破壞過(guò)程是漸變性的,是變形積累到一定程度表現(xiàn)出宏觀滑移的一個(gè)非線性復(fù)雜過(guò)程,如邊坡滑動(dòng)蠕動(dòng)或擋土墻后楔形巖土體的開(kāi)裂滑動(dòng),巖土體物理力學(xué)特征和地質(zhì)環(huán)境因素對(duì)其都有影響,這些影響因素有的是確定的,有的是隨機(jī)的,它們對(duì)不同類型邊坡穩(wěn)定性的影響權(quán)重也是不同的,之間又有復(fù)雜的非線性關(guān)系[1-2]。運(yùn)用現(xiàn)代智能方法如人工神經(jīng)網(wǎng)絡(luò)已成為預(yù)測(cè)邊坡穩(wěn)定性的一種較有效的手段,其特點(diǎn)是智能性、綜合性、集成性和非線性。

常用的BPNN(誤差反向傳播神經(jīng)網(wǎng)絡(luò))及其改進(jìn)方法無(wú)法自動(dòng)調(diào)整結(jié)構(gòu)組成,性能優(yōu)良的BPNN需要優(yōu)化網(wǎng)絡(luò)結(jié)構(gòu),優(yōu)化權(quán)值、閾值等參數(shù),選擇合理的計(jì)算方法和學(xué)習(xí)參數(shù)。這些都用到了相關(guān)的優(yōu)化算法,例如用遺傳或粒子群算法對(duì)未知參數(shù)尋優(yōu),必要時(shí)還要擴(kuò)展網(wǎng)絡(luò)結(jié)構(gòu)以減小系統(tǒng)誤差,同時(shí)收斂速度較慢,這會(huì)限制它在實(shí)際中的應(yīng)用和推廣。廣義回歸神經(jīng)網(wǎng)絡(luò)(GRNN)結(jié)構(gòu)設(shè)計(jì)簡(jiǎn)單,收斂速度快,所需訓(xùn)練樣本少,對(duì)被建模對(duì)象的先驗(yàn)知識(shí)要求不多,具有全局逼近性和最佳逼近性質(zhì),魯棒性及非線性處理能力強(qiáng),能根據(jù)樣本數(shù)據(jù)反映其中隱含的映射關(guān)系,且不存在局部最小問(wèn)題,目前已在工程中得到了應(yīng)用[3-4]。

GRNN唯一需要調(diào)整的參數(shù)是光滑因子,它的選擇對(duì)于網(wǎng)絡(luò)性能優(yōu)劣有較大影響,光滑因子越小,擬合程度越好,但過(guò)小會(huì)導(dǎo)致過(guò)擬合。文獻(xiàn)[5-7]選取了光滑因子試算范圍內(nèi)的最小值,因?yàn)樽钚≈挡坏扔谧顑?yōu)值,故直接應(yīng)用某范圍內(nèi)的最小值是不準(zhǔn)確的,會(huì)導(dǎo)致網(wǎng)絡(luò)泛化能力差。筆者應(yīng)用遍歷樣本的交叉驗(yàn)證方法,可以合理地選擇光滑因子值,改善網(wǎng)絡(luò)泛化能力,提高預(yù)測(cè)精度。

1 GRNN基本理論

GRNN是一種建立在非參數(shù)估計(jì)基礎(chǔ)上的非線性回歸的徑向基神經(jīng)網(wǎng)絡(luò),不需要事先確定方程形式,而以概率密度函數(shù)代替固有的方程形式,直接計(jì)算出因變量對(duì)自變量的回歸值。其優(yōu)勢(shì)在于不需要重復(fù)訓(xùn)練,網(wǎng)絡(luò)建成的同時(shí)訓(xùn)練即完成,網(wǎng)絡(luò)的訓(xùn)練過(guò)程實(shí)際上就是確定光滑因子的過(guò)程,并且在網(wǎng)絡(luò)數(shù)據(jù)稀少時(shí)效果也較好,能夠收斂于樣本量聚類較多的優(yōu)化回歸面。網(wǎng)絡(luò)輸入層只傳遞輸入向量到徑向基層,隱含層中神經(jīng)元個(gè)數(shù)由所描述的問(wèn)題而定,通常傳遞函數(shù)采用高斯函數(shù)radbas:

式中:aj為經(jīng)過(guò)高斯函數(shù)傳遞后的網(wǎng)絡(luò)輸出;nprod為規(guī)范化點(diǎn)積權(quán)函數(shù),是線性輸出層的權(quán)值函數(shù);‖dist‖為歐氏距離函數(shù),即該層權(quán)值函數(shù);bj為第j個(gè)隱含層與光滑因子有關(guān)的閾值;σj為光滑因子(spread),它決定第 j個(gè)隱含層位置處基函數(shù)的形狀,σj越大基函數(shù)越平滑。

GRNN的每次訓(xùn)練都會(huì)自動(dòng)檢查輸出誤差,所產(chǎn)生的最大誤差對(duì)應(yīng)的輸入向量會(huì)作為權(quán)值產(chǎn)生一個(gè)新的隱含層神經(jīng)元,然后,新網(wǎng)絡(luò)會(huì)循環(huán)檢查誤差直至神經(jīng)元數(shù)量達(dá)到最大或達(dá)到一定精度為止。

初始化即訓(xùn)練樣本的學(xué)習(xí)過(guò)程,學(xué)習(xí)樣本確定了,則相應(yīng)的網(wǎng)絡(luò)結(jié)構(gòu)和各神經(jīng)元之間的連接權(quán)值也隨之自動(dòng)確定,網(wǎng)絡(luò)訓(xùn)練過(guò)程實(shí)際上是確定光滑因子的過(guò)程。較BPNN而言,GRNN的人為調(diào)節(jié)參數(shù)僅為1個(gè),網(wǎng)絡(luò)學(xué)習(xí)全部依賴于數(shù)據(jù)樣本,這就決定了網(wǎng)絡(luò)得以最大限度地避免人為主觀假定對(duì)計(jì)算結(jié)果的影響。同時(shí)GRNN解決了BPNN訓(xùn)練時(shí)間長(zhǎng)且確定隱含層數(shù)目難的問(wèn)題,能穩(wěn)定地描述系統(tǒng)的特征。

2 光滑因子的影響分析與選取方法

2.1 光滑因子的影響

一般情況下,訓(xùn)練能力差時(shí)網(wǎng)絡(luò)的預(yù)測(cè)能力也差,并且在一定程度上隨著訓(xùn)練能力的提高預(yù)測(cè)能力也會(huì)提高,但這種趨勢(shì)有一個(gè)極限,達(dá)到此極限后,隨著訓(xùn)練能力的提高,預(yù)測(cè)能力反而下降,即出現(xiàn)所謂過(guò)適性,也稱為過(guò)擬合,此時(shí)網(wǎng)絡(luò)學(xué)習(xí)了過(guò)多的樣本細(xì)節(jié)而不能反映樣本內(nèi)在的規(guī)律。泛化能力差會(huì)造成不適性,過(guò)適性和不適性的網(wǎng)絡(luò)都屬于不成熟網(wǎng)絡(luò),仿真效果較差[8]。

創(chuàng)建輸入輸出樣本和廣義回歸神經(jīng)網(wǎng)絡(luò),輸入樣本在[-1,1]區(qū)間內(nèi)均勻地取21個(gè)點(diǎn),21個(gè)數(shù)據(jù)點(diǎn)坐標(biāo)如圖1所示。當(dāng)光滑因子取較小值0.02時(shí),用步長(zhǎng)0.01來(lái)檢驗(yàn)擬合效果,觀察所選光滑因子是否能夠體現(xiàn)出所給樣本內(nèi)在的規(guī)律性。從圖1(a)中可以看出,網(wǎng)絡(luò)記住了訓(xùn)練樣本細(xì)節(jié),甚至個(gè)別噪聲,曲線較陡,在原始樣本點(diǎn)處形成平臺(tái),附近的數(shù)值向其值靠攏。當(dāng)光滑因子取較大值0.2時(shí),從圖1(b)可以看出,網(wǎng)絡(luò)進(jìn)行函數(shù)逼近時(shí)擬合效果較差,出現(xiàn)了不適性。總體來(lái)說(shuō),光滑因子值越小,擬合越好,曲線越不光滑,但光滑因子太小時(shí)不能學(xué)習(xí)到真正的規(guī)律性,這樣就對(duì)測(cè)試樣本或仿真樣本不敏感,即表現(xiàn)出過(guò)適性,以此網(wǎng)絡(luò)來(lái)推廣仿真勢(shì)必會(huì)造成較大的誤差。

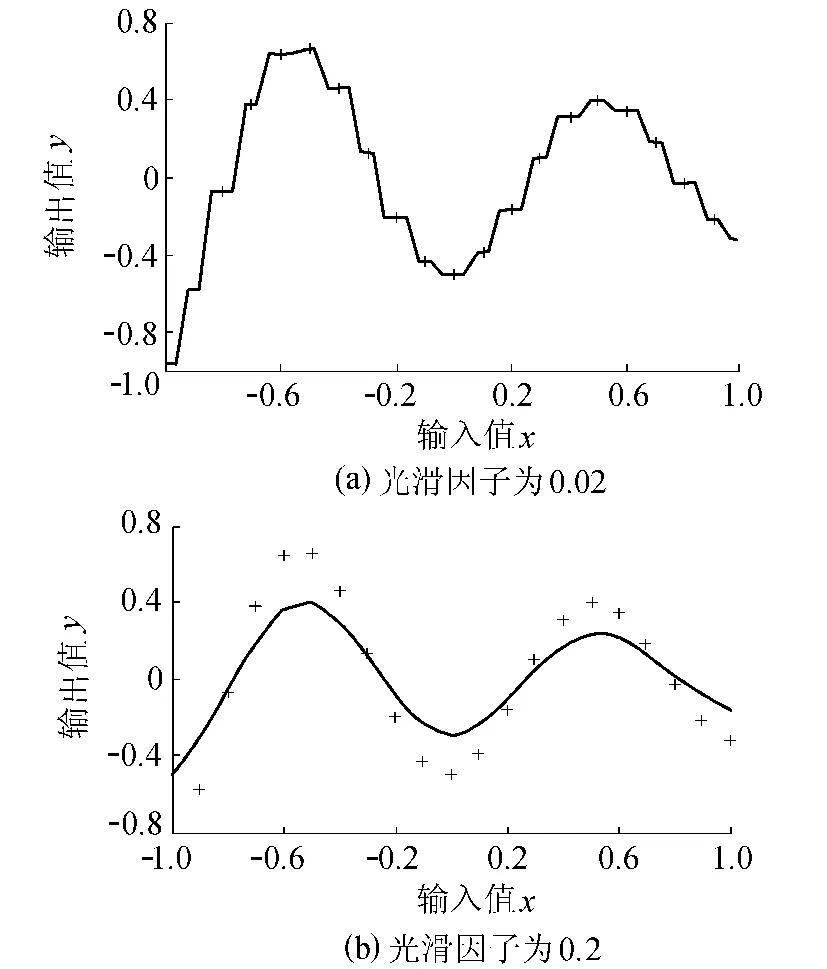
圖1 訓(xùn)練樣本的過(guò)適性與不適性

2.2 光滑因子的選取

采用LOO交叉驗(yàn)證方法評(píng)估模型的預(yù)測(cè)能力,即在一定范圍內(nèi)以某一步長(zhǎng)遞增變化,在學(xué)習(xí)樣本中以1個(gè)樣本作為估計(jì)樣本,剩余的樣本采用構(gòu)造的GRNN對(duì)估計(jì)樣本仿真,對(duì)所有樣本都遍歷1次,得到預(yù)測(cè)值與樣本值之間的誤差序列,以序列均方誤差值作為網(wǎng)絡(luò)的評(píng)價(jià)指標(biāo),將最小誤差對(duì)應(yīng)的光滑因子作為最終所選值。光滑因子的確定過(guò)程符合整體偏差最小原則[9-11]。

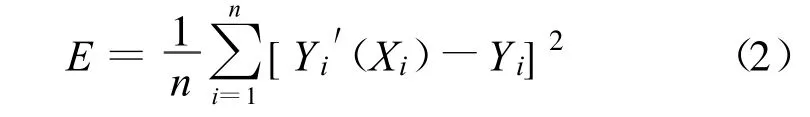
式中:E為預(yù)測(cè)值與樣本期望值的方差;Xi為第i個(gè)樣本對(duì)應(yīng)的輸入值;Yi′(Xi)為第 i個(gè)樣本的預(yù)測(cè)值;Yi為樣本期望值;n為樣本個(gè)數(shù)。

訓(xùn)練樣本中選擇某列數(shù)組作為估計(jì)樣本,用剩余的樣本構(gòu)造學(xué)習(xí)樣本,依次對(duì)所有樣本遍歷1次,具體表達(dá)如式(3)、式(4)所示:

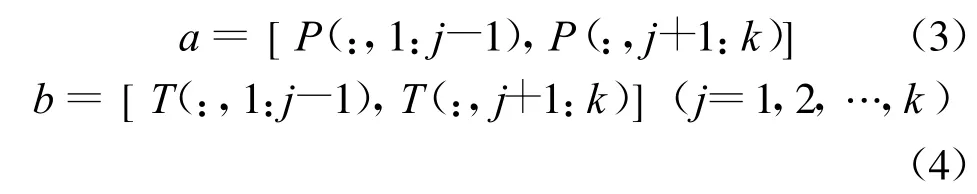
式中:a,b分別為訓(xùn)練樣本和期望樣本;P為輸入樣本;T為輸出樣本;k為輸入或輸出數(shù)組的列數(shù),可以控制光滑因子的精度。

應(yīng)用上面所示的樣本可以求得光滑因子迭代值,其中用訓(xùn)練樣本a代替輸入樣本P,用期望樣本b代替輸出樣本T,即依次取出j列作為測(cè)試樣本,剩余所有列作為訓(xùn)練樣本,仿真后與理論值或?qū)崪y(cè)值比較。

在確定平滑因子的過(guò)程中,初始值選取太小,式(4)可能出現(xiàn)除數(shù)為零的情況,文獻(xiàn)[3]給出了初始值的計(jì)算公式:

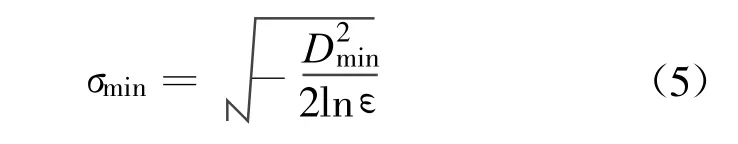
式中:σmin為光滑因子選取區(qū)間的初始值;Dmin為學(xué)習(xí)樣本中各輸入樣本之間Euclid距離的最小值;ε為計(jì)算機(jī)能夠表達(dá)的最小正數(shù)。

以步長(zhǎng)為0.01檢驗(yàn)網(wǎng)絡(luò)的擬合情況,選用誤差最小時(shí)對(duì)應(yīng)的光滑因子(此時(shí)光滑因子為0.058),網(wǎng)絡(luò)仿真與訓(xùn)練樣本如圖2所示,擬合效果較好。對(duì)于一般問(wèn)題,按照上述方法確定的平滑參數(shù)即可滿足要求,也可建立優(yōu)化問(wèn)題模型,并應(yīng)用傳統(tǒng)和新型優(yōu)化方法解決該問(wèn)題。

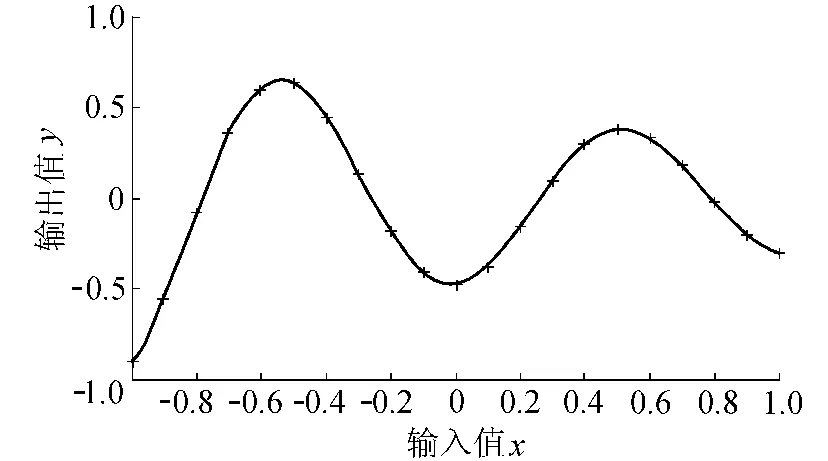
圖2 GRNN的逼真函數(shù)

3 應(yīng)用實(shí)例及模型對(duì)比分析

為了得到比較好的預(yù)測(cè)效果,一般在網(wǎng)絡(luò)訓(xùn)練前應(yīng)對(duì)原始數(shù)據(jù)作預(yù)處理,包括剔除離散性較大的值,對(duì)數(shù)量級(jí)差別較大的數(shù)據(jù)作歸一化或標(biāo)準(zhǔn)化處理,對(duì)輸出向量作反處理變換至原單位(如不存在相對(duì)于其他輸入樣本特別大或特別小的樣本矢量可不進(jìn)行歸一化)。歸一化時(shí)對(duì)輸入輸出向量正則化處理,使其落入[-1,1]區(qū)間,或歸一到其單位方差和零均值,計(jì)算完畢后需要對(duì)結(jié)果數(shù)據(jù)還原。簡(jiǎn)單歸一化和反歸一化方法處理見(jiàn)式(6)、式(7):

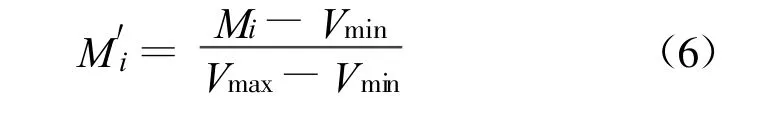
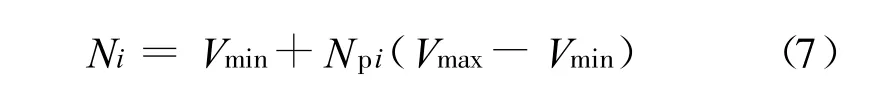
式中:Mi為原始輸入值;M′i為歸一化后的網(wǎng)絡(luò)輸入值;N p i為在[0,1]區(qū)間的預(yù)測(cè)值;Ni為預(yù)測(cè)值的還原值;Vmin和Vmax分別為樣本最小值和最大值。

算例 對(duì)82個(gè)實(shí)際工程邊坡的極限平衡分析統(tǒng)計(jì)資料和邊坡對(duì)應(yīng)狀態(tài)(表1)分析可以發(fā)現(xiàn),由于分析信息的模糊性、不確定性,即使計(jì)算安全系數(shù)大于1.6,也有部分邊坡最終發(fā)生失穩(wěn)破壞。訓(xùn)練樣本為密度 ρ、黏聚力c、摩擦角 φ、殘余摩擦角 ψ及坡高Η,目標(biāo)樣本為安全系數(shù)和穩(wěn)定狀態(tài)。邊坡穩(wěn)定狀態(tài)為0代表破壞,1代表穩(wěn)定,利用GRNN具備的聚類分類原理可以初步評(píng)判邊坡穩(wěn)定狀態(tài)。

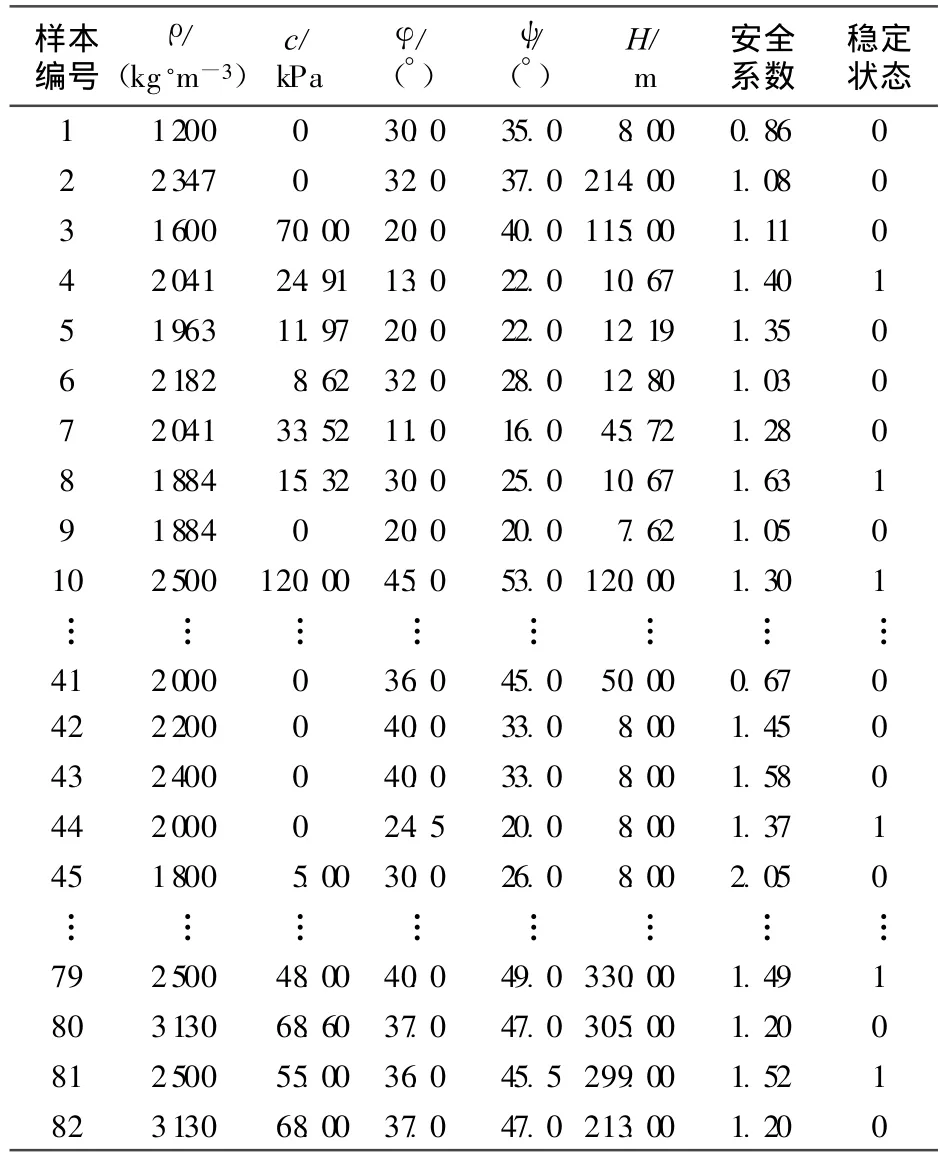
表1 82個(gè)實(shí)際工程邊坡的統(tǒng)計(jì)資料與邊坡穩(wěn)定狀態(tài)

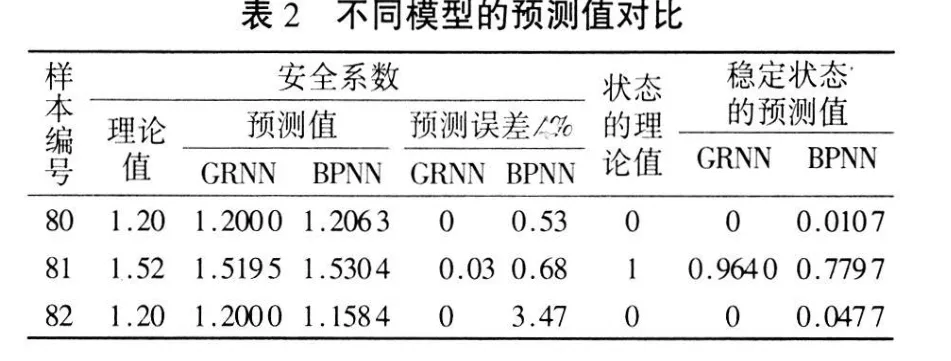
樣本1～79作為訓(xùn)練樣本,樣本80～82作為測(cè)試樣本。對(duì)樣本歸一化處理后GRNN迭代搜索出的平滑因子值為0.143,安全系數(shù)預(yù)測(cè)結(jié)果為1.2000,1.5195,1.2000;BPNN的預(yù)測(cè)結(jié)果為1.2063,1.5304,1.1584,模型的預(yù)測(cè)結(jié)果如表2所示。從表2可以看出,即使存在安全系數(shù)大于1.6而產(chǎn)生破壞的干擾樣本(表1中樣本45),但總體預(yù)測(cè)情況仍然是良好的,GRNN預(yù)測(cè)的安全系數(shù)誤差很小,最大為0.03%,而B(niǎo)PNN預(yù)測(cè)的安全系數(shù)最大誤差不超過(guò)3.5%。另外GRNN在計(jì)算過(guò)程中的快捷更顯示了其優(yōu)越性。

?

4 結(jié) 語(yǔ)

a.討論了GRNN網(wǎng)絡(luò)中光滑因子的影響,光滑因子選取不當(dāng)會(huì)造成網(wǎng)絡(luò)的泛化能力差。根據(jù)光滑因子的初值,提出使用LOO交叉驗(yàn)證方法將得到的序列均方誤差值作為網(wǎng)絡(luò)的評(píng)價(jià)指標(biāo),最小誤差對(duì)應(yīng)的光滑因子即為所選值,并驗(yàn)證了該方法的合理性。

b.搜集了82個(gè)圓弧滑動(dòng)邊坡穩(wěn)定性樣本,由于分析信息的模糊性、不確定性,即使計(jì)算安全系數(shù)大于1.6也有部分邊坡最終發(fā)生失穩(wěn)破壞。結(jié)合本文提出的光滑因子選取方法,應(yīng)用GRNN模型進(jìn)行預(yù)測(cè)分析,吻合效果較好,反演精度較高,網(wǎng)絡(luò)操作簡(jiǎn)捷,易為工程人員接受,可在工程實(shí)際中應(yīng)用。

c.由于GRNN具有較強(qiáng)的函數(shù)擬合和逼近能力,其對(duì)樣本依賴性強(qiáng)的特點(diǎn)使得選取具有代表性的訓(xùn)練樣本數(shù)據(jù)非常重要,如果預(yù)測(cè)誤差過(guò)大可能是數(shù)據(jù)的問(wèn)題,關(guān)于如何減小訓(xùn)練樣本數(shù)據(jù)中的誤差或噪聲對(duì)預(yù)測(cè)精度的影響需做進(jìn)一步研究。

[1]狄圣杰,徐衛(wèi)亞.黏性土求主動(dòng)土壓力的庫(kù)爾曼法及應(yīng)用[J].巖土工程學(xué)報(bào),2010,32(6):970-974.

[2]張玉,張方方.變水位多工況下大型渠道土質(zhì)邊坡的穩(wěn)定分析[J].水利水電科技進(jìn)展,2010,30(1):56-60.

[3]TOMANDL D,SCHOBER A.A modified general regression neural network with new efficient training algorithms as a robust‘black box' tool for data analysis[J].Neural Networks,2001,14(4):1023-1034.

[4]周昊,鄭立剛,樊建人,等.廣義回歸神經(jīng)網(wǎng)絡(luò)在煤灰熔點(diǎn)預(yù)測(cè)中的應(yīng)用[J].浙江大學(xué)學(xué)報(bào):工學(xué)版,2004,38(11):1470-1482.

[5]蘭海濤,李謙,韓春雨.基于廣義回歸神經(jīng)網(wǎng)絡(luò)的邊坡穩(wěn)定性評(píng)價(jià)[J].巖土力學(xué),2009,30(11):3460-3463.

[6]周建萍,閆澍旺.廣義回歸神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)加筋土支擋結(jié)構(gòu)高度[J].巖土力學(xué),2002,23(4):486-490.

[7]馮志鵬,宋希庚,薛冬新,等.基于廣義回歸神經(jīng)網(wǎng)絡(luò)的時(shí)間序列預(yù)測(cè)研究[J].振動(dòng)、測(cè)試與診斷,2003,23(2):105-144.

[8]DI Sheng-jie,XU Wei-ya,WEI Qing.The selection of spread and the application in engineering of GRNN[C]//Proceedings of 2nd International Conference on Information Science and Engineering.Hangzhou:IEEE,2010:5508-5511.

[9]BROOMHEAD D S,LOWE D.Multivarialble functional interpolation and adaptive networks[J].Complex System,1988,2:321-355.

[10]SPECHT D F.A general regression neural network[J].IEEE Transactions on Neural Network,1991,2:568-576.

[11]DING D X,ZHANG Z J.Artificial neural network based inverse design method for circular sliding slopes[J].J Cent South Univ Technol,2004,11(1):89-92.