數字控制系統等效模擬校正調試研究

王曉麗，趙艷花，周 陽

（1. 洛陽理工學院 電氣工程與自動化系，洛陽 471023；2. 同濟大學 電子與信息工程學院，上海 200092）

數字控制系統等效模擬校正調試研究

王曉麗1，趙艷花1，周 陽2

（1. 洛陽理工學院 電氣工程與自動化系，洛陽 471023；2. 同濟大學 電子與信息工程學院，上海 200092）

0 引言

隨著計算機在控制系統中的應用，越來越多的控制系統實際是一個數字控制系統。數字控制系統中的控制器的直接設計方法[1]和解析設計方法[1]均需要事先得知實際系統精確的數學模型，而實際系統總會和系統模型之間存在差別，這使得用脈沖傳遞函數表示的數字控制系統在調試時會出現參數之間關系耦合、參數更改與系統特性之間表現不直觀的特點，因此用脈沖傳遞函數的表示方法多見于系統模型的分析與設計過程中，而少見于工程現場的程序實現與調試。傳統頻域分析法由于概念清楚和方便調試，很多時候還廣泛的為科研和工程人員所使用[2-5]，特別是因為PID法和頻域響應法校正均有成熟的經驗和步驟可以參考。等效模擬校正設計方法[1]正是根據連續系統性能指標為某個等價的連續系統設計一個模擬校正裝置，然后再通過某種轉化方法將模擬校正裝置傳遞函數變換為等效的數字控制器脈沖傳遞函數。轉化的方式有后向差分，梯形積分兩種方法。增量的PID[7]概念清楚，調試步驟明確，便于計算機內實現，本文受其啟發，基于等效模擬校正方法的滯后超前校正方法，設計出通用的流程，并分析了配合參數與滯后超前校正參數之間的定量關系。為數字控制系統的設計和調試提供快速方法。本方法和增量式PID算法具有同樣優點，有很高的推廣應用價值。

1 頻域法校正及等效方法

線性控制系統一般由多個閉環組成的。如伺服控制系統是由電流環、速度環、位置環組成的三閉環結構。為了簡化分析，本文以三閉環中速度環為例，其它閉環的分析方法相同。典型的伺服控制系統速度環如圖1所示[8]。G（s）是控制器的傳遞函數，G0（s）是電機的傳遞函數。

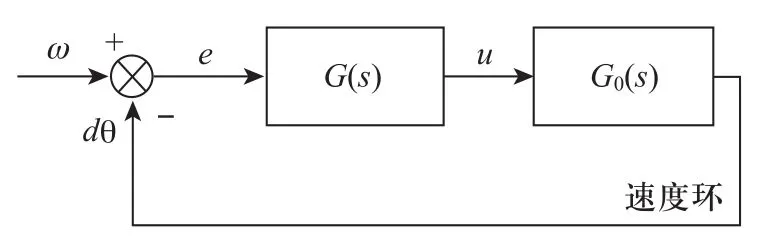
圖1 單閉環控制系統

為了把控制系統校正為I型或II型系統，可用的頻域響應法校正方法有多種。本文僅考慮串聯校正中的滯后校正、超前校正、滯后超前校正和PID的等價形式共四種類型。為了分析的簡潔，本文假定增益等于1。對于實際系統，可用傳遞函數轉化求等效偏差 的方法使得增益等于1，如圖2所示。

頻域響應校正方法中典型的校正環節有超前校正、滯后校正、滯后超前校正等。其公式表述如式（1）－式（4）。

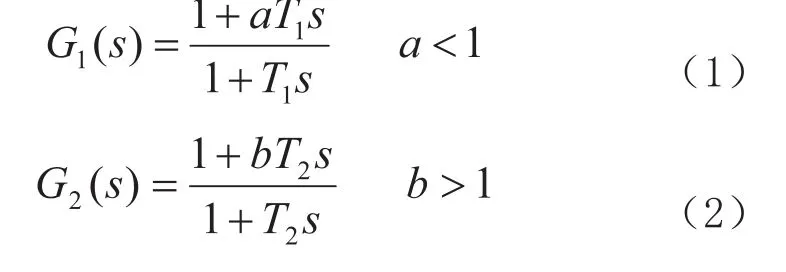
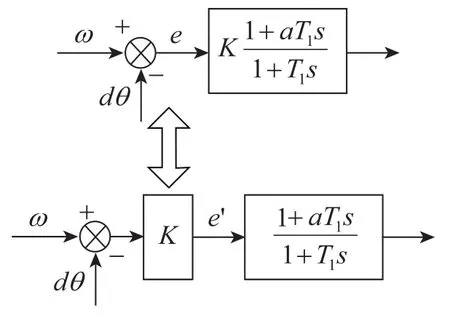
圖2 假定增益為1的等效關系圖

其中， a＜1，b＞1。

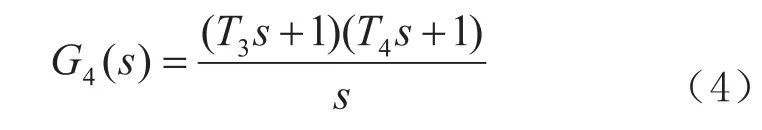
等效模擬校正設計方法中常用的轉化方式有后向差分，梯形積分兩種。其表達式為：

將式（5）分別代入式（1）－式（4），可得到式（7）－式（10）一組轉化結果。

可以看出，當式（9）中某些參數取特定的值時，可以得到式（7）、式（8）。伺服控制系統設計時，時常使用P、PI或PD控制率，將這些控制率等效成典型校正環節后，再與式（7）相比，可以得到參數配合關系如表1所示。因此，可以認為式（9）是式（7）、式（8）、式（10）的統一形式。所以，下文以式（9）為例做出分析。

表1 典型校正環節參數配合關系表

由文獻[9]對脈沖傳遞函數的分析，可知：

對比式（9）和式（11），可以得出：

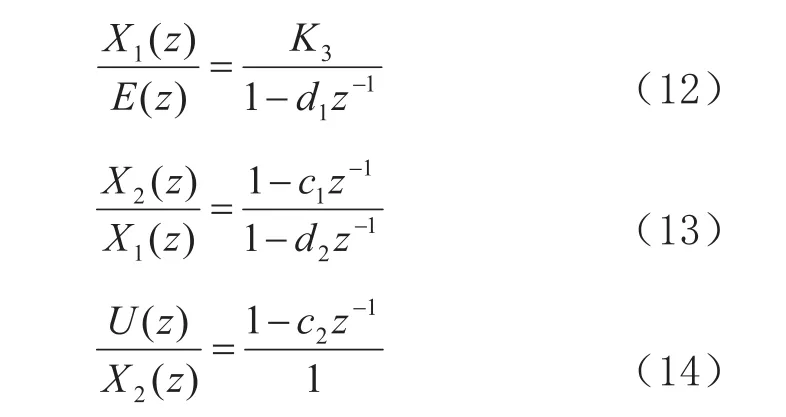
由式（12）－式（14）轉化為對應的脈沖傳遞函數可為：

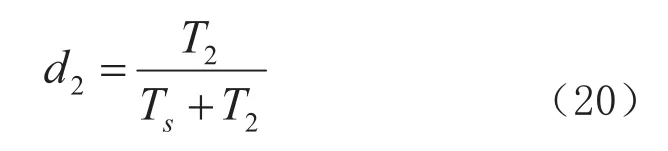
至此，頻域分析法校正的四種常用形式在式（5）的條件下統一的程序流程可以得出，如圖3所示。可以看出，圖 3 中 x1（k），x2（k），u（k）的意義和式（15）相同。同樣的分析，可以得出式（6）轉化式（1）－式（4）的程序流程一致，僅是參數配合關系不同。在此限于篇幅，具體過程從略。

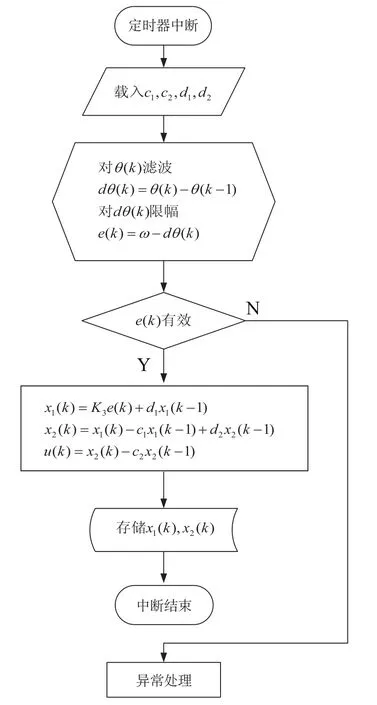
圖3 滯后超前校正等效模擬方法流程圖

2 調試方法分析

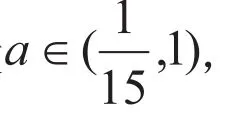
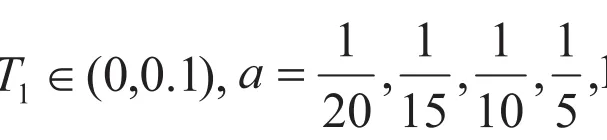
表2 參數配合趨勢

圖4 參數c1與參數T1，a典型值的配合關系

3 結論

圖5 參數d1與參數T1，a典型值的配合關系

本文推得出了數字控制系統可用的滯后超前校正統一形式，并給出了典型環節的參數配合解析式和程序流程圖，并指出參數變化的配合關系。解決了數字控制系統中脈沖傳遞函數描述方法在調試過程中參數修改直觀性不強的問題。本方法和增量式PID具有同樣的優點，為科研和工程技術人員快速設計和調試控制系統提供幫助，有重要推廣應用價值。

[1]吳麟. 自動控制原理[M]. 北京: 清華大學出版社. 2004:25-131.

[2]Fulford, Adam.An embedde mechatronic system for wireless servo control[J]. Proceedings of the American Control Conference, 2002, 2: 1658-1659.

[3]王連明, 機載光電平臺的穩定與跟蹤伺服控制技術研究[D], 長春: 中國科學院長春光學精密機械與物理研究所,2002: 60-65.

[4]龐新良. 機載光電穩定平臺數字控制關鍵技術研究[D].長沙: 國防科技大學, 2007: 51-61.

[5]陳占軍. 基于DSP伺服系統位置環的設計[J]. 機床與液壓. 2007, 35(7): 165-167.

[6]周陽, 董國華. 光電紅外成像消旋系統測控技術研究[J].機電工程. 2010, 27(1): 4-8.

[7]劉金錕. 先進PID控制及其MATLAB[M]. 北京: 電子工業出版社. 2004: 35-42.

[8]Hirata, Mitsuo. Servo performance enhancement of motion system via a quantization error estimation method-Introduction to nanoscale servo control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(10): 3817-3824.

[9]張琛. 精密定位技術[M].上海：上海交通大學.1992.

[10]李友善. 自動控制原理[M]. 北京: 國防工業出版社.2007: 252-260

Equivalent analog correction debuging method of digital control system

WANG Xiao-li1, ZHAO Yan-hua1, ZHOU Yang2

針對脈沖傳遞函數描述方法在調試過程中參數修改直觀性不強的問題，根據數字控制系統中等效模擬校正方法能夠將模擬校正裝置傳遞函數變換為等效的數字控制器脈沖傳遞函數的特點，推導出滯后超前校正的統一形式，指出了典型環節的參數配合解析式及相應的參數變化范圍，給出用等效模擬校正方法轉化后的滯后超前校正的程序流程圖，并指出參數變化的配合關系。研究結果表明，該方法具有概念清楚，調試步驟明確，便于計算機實現等優點。為科研和工程技術人員快速設計和調試控制系統提供幫助。

滯后超前校正；PID校正；數字控制系統；雙線性變換

王曉麗（1980－），女，河南禹州人，助教，碩士，研究方向為智能控制技術，現代測控技術與系統。

TP273

A

1009-0134(2011)4(下)-0013-04

10.3969/j.issn.1009-0134.2011.4(下).05

2011-02-28