不平衡負載條件下三相四橋臂逆變器的控制

費蘭玲，張 凱，蔡院玲

(華中科技大學電氣與電子工程學院，湖北武漢430074)

1 概述

基于三相四線制逆變器拓撲結構，提出的三相四橋臂逆變器(four－leg inverter，FLI)廣泛應用于功率變換和UPS等場合。它具有直流母線電壓低，開關損耗小，可以接非線性及不平衡負載等優點。較之于傳統的三相三橋臂逆變器，三相四橋臂逆變器通過添加第四條橋臂為非線性及不平衡負載零序電流提供通路，保證逆變器在各種惡劣負載條件下，仍能給負載端提供三相平衡的正弦電壓。其主電路圖如圖1所示。

在原有三相三橋臂逆變器拓撲結構上發展而來的三相四橋臂逆變器，增加了兩個開關管(即:兩個開關狀態)，開關狀態由原來的2^3增加為2^4。與傳統逆變器相比較，控制方法更加復雜，這在一定程度上局限了三相四橋臂逆變器的應用。新增加的第四橋臂與其它三相共用，形成三相電流回路，因此對其它三相橋臂開關的觸發和輸出電流的激勵產生牽制作用。解除牽制的方法有兩個:一是把中性點橋臂與其它三相橋臂分開，單獨采用中性點電流進行控制，其余三相橋臂仍可以采用成熟的三橋臂控制方式，如文獻［1，2］中采用的調制方式;另一種是把中性橋臂與其余橋臂一起進行協調控制，常見的控制策略如:諧波注入式PWM脈寬調制，3D －SVPWM 脈寬調制技術［3，4］。由于典型的SVPWM調制實質上是一種注入零序分量的三相PWM調制方式［5］，在線性調制范圍內，零序分量注入的PWM調制方式最大調制比m≤2/，直流母線電壓利用率提高15%。本文中關于不平衡負載條件下的三相四橋臂逆變器控制，即是基于零序分量注入的PWM調制方式。三相四橋臂逆變器具有外接不平衡負載能力。然而在實際應用中，由于系統各相硬件環境及控制策略等因素的影響，在不平衡負載條件下逆變器系統輸出三相電壓仍會有一定程度的不平衡。為進一步改善逆變器系統在嚴重不平衡負載情況下輸出電壓的對稱性，減小輸出電壓不平衡度，本文提出一種新穎的控制策略——旋轉坐標系下的PIR-P雙環控制，并詳細介紹了系統模型、控制思想、控制器設計、對比仿真等內容。

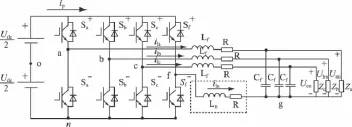
圖1 三相四橋臂逆變器主電路圖

2 三相四橋臂逆變器系統建模

圖1中，中性電感Ln主要用于濾除中性電流的開關紋波。此電路采用平均周期法建立靜止坐標系下數學模型，負載電流作為外部擾動，輸入電源為理想的三相對稱正弦信號，以空載情況為例建立數學模型。假定開關管為理想器件，忽略死區效應。上管導通時開關函數為 1，下管導通時開關函數為 0。ila、ilb、ilc、iln分別為A、B、C相及第四橋臂上流進濾波電感的相電流，Udc表示直流母線電壓，Lf，Cf為逆變輸出的濾波電感和濾波電容，R為濾波電感及死區效應等效電阻，Ln為中性電感(且 Ln=Lf)，Uan、Ubn、Ucn為三相對稱輸出逆變電壓。Si(i=a，b，c，n)均表示各個橋臂上開關管狀態表示的開關函數。

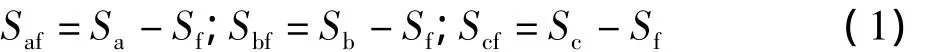
假設式(1)中忽略開關頻率諧波分量的影響，根據開關周期平均的運算方法，即可得到三相橋臂相對第四橋臂的占空比daf、dbf、dcf。對電流回路進行分析得到:

綜合上式，用矩陣方程表示為:

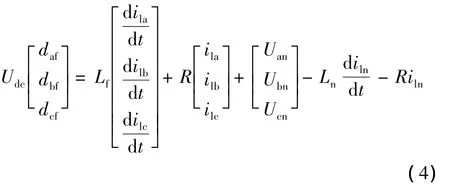
以空載情況下建立數學模型，可得到:

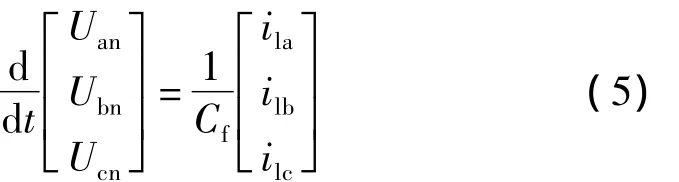
從上述三相四橋臂逆變器在靜止坐標系下的數學模型不難發現，當第四橋臂上的中性電感及等效電阻不可忽略時，三相靜止坐標系下的三相四橋臂逆變器是一個強耦合系統。A、B、C三相橋臂共用第四橋臂為不平衡負載條件下的零序電流提供通路，三相四橋臂逆變器不能簡單等效為三個相互獨立的單相全橋逆變器系統。且控制量均為時變的交流量，不利于控制器設計。在此基礎上，可將三相靜止坐標系下得到的系統數學模型，通過坐標變換，轉換到以逆變電源基波頻率同步旋轉的旋轉坐標系下。經坐標變換后，靜止坐標系下的基波正弦量變換為直流量，利于控制器設計。由靜止坐標系轉換到旋轉坐標系下的變換矩陣為:

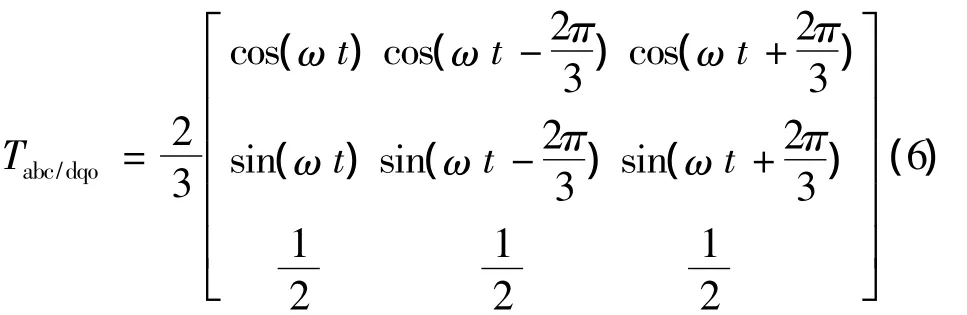
其變換逆矩陣為:

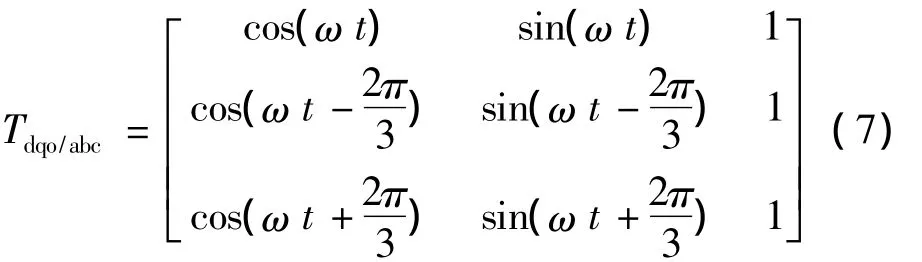
在等式(4)，(5)兩邊同時乘以變換矩陣Tabc/dqo，綜合后得到:

式中，Ud、Uq、Uo;id、iq、io;dd、dq、do分別為逆變輸出三相電壓，三相電感電流，及三相調制占空比在旋轉坐標系下 d、q、o軸上的分量。

根據式(8)、(9)，不難得到旋轉坐標系下三相四橋臂逆變器解耦后系統動態補償框圖，如圖2所示。

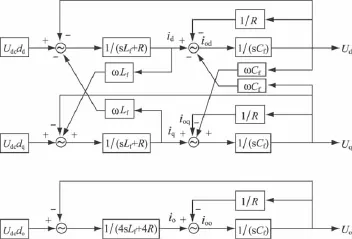
圖2 旋轉坐標系下系統動態補償框圖

解耦完成后，三相四橋臂逆變器可以轉化為三個單相逆變器進行獨立控制。采用傳統的電流內環電壓外環的雙環控制策略，即可獲得良好的控制效果。調節器的設計可以根據各自獨立的數學模型進行設計。需要指出的是，解耦后o軸的數學模型參數不同于d、q軸，設計時需引起注意。

當三相四橋臂逆變器接不平衡負載時，三相負載不平衡電流轉換到d、q軸上不僅含有直流分量，還含有由正序和負序分量轉換而來的二次基波頻率正弦量，且零序分量全部轉換為o軸上的基波頻率的正弦量。此時采用PI-P雙環控制，不能發揮旋轉坐標系下控制的優勢，系統仍有穩態誤差。可考慮電壓外環采用PIR控制器，在抑制基波頻率及其基波倍頻分量影響的同時，可有效改善系統的穩態誤差，實現無靜差控制。其三相四橋臂逆變器的綜合控制框圖如圖3所示。

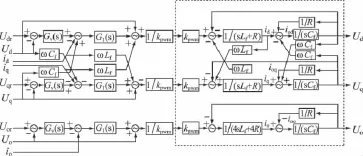
圖3 三相四橋臂逆變器系統控制框圖

3 PIR+P雙閉環控制策略

基于內模原理的諧振控制器，將系統信號的動態模型包含在控制系統中，相當于一個信號發生器，它在固定頻率點實現無限大增益，對很小的誤差信號進行實時控制，可實現對參考信號的完美跟蹤。基于此原理的重復控制器，將基波參考信號內模和諧波次頻率包含在系統中，與其他控制策略組合而成的復合控制器，已廣泛應用于逆變器的非線性負載控制，可獲得良好的動態和穩態性能。針對諧振控制器在固定頻率點增益無限大的特點，將其與傳統的PI-P雙環控制器配合使用，P環節用于提高系統動態性能，I環節可以增加系統阻尼，提高系統穩態精度，R諧振環節用于對特定頻率點mωe進行控制，以實現對角頻率mωe的交流信號的無靜差跟蹤。因而，PI部分用以保證整個系統的動態性能和穩定裕度，諧振環節R的零點可提供一定的超前相角用以保證系統的相位裕度和穩態性能。其基本的控制器結構形式為:

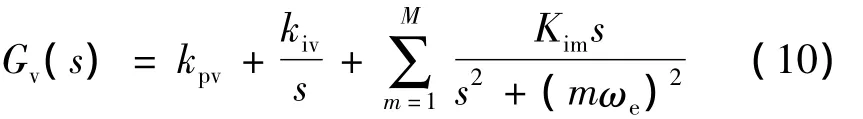
三相四橋臂逆變器外接不平衡負載時，不平衡負載電流在d、q、o軸上的分量除直流分量外，還分別包括兩次基波頻率分量和基波頻率分量的正弦量，PI控制器不能實現穩態無靜差控制。當電壓外環采用PIR控制器時，d、q、o軸電壓控制器在原有PI控制器基礎上，分別添加含有2次、2次、1次基波頻率交流信號內模的諧振控制器。利用諧振控制器在這些頻率點增益較大的優點，對負序和零序分量產生的交流控制信號進行調節。可有效改善系統的穩態精度，實現理想情況下的無靜差跟蹤。以d軸控制器為例進行分析，解耦后其d軸控制結構框圖見圖4。

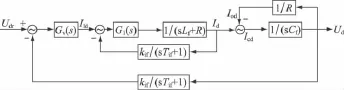
圖4 d軸控制器原理框圖

3.1 電流內環控制器設計

對電流控制器的設計考慮到變換器的延時和PWM調節的小慣性環節，其電流內環控制框圖見圖5。

圖5 電流內環控制器原理框圖

圖5中，kR=1/R;TL=L/R;kip表示電流內環比例控制器參數;Kpwm、Ts表示變換器放大系數和時間濾波常數，Ts通常取開關頻率的一半;kif、Tif分別表示電流反饋通道比例放大系數和時間濾波常數。則電流內環的開環傳遞函數為:

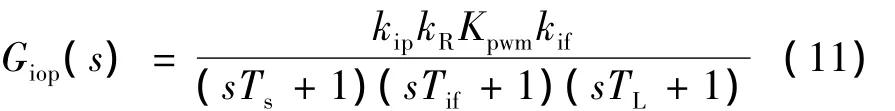
依據自動控制系統的工程化設計方法，Ts、Tif均為小時間常數，可以一個一階環節替代這兩個慣性環節，假設用于替代的一階環節時間常數為Tsf=Ts+Tif。當TL≥Tsf時，可將大慣性環節近似處理為積分環節。進而得到簡化后的電流內環的控制器為一典型的Ⅰ型系統，具有快速的跟蹤性能:

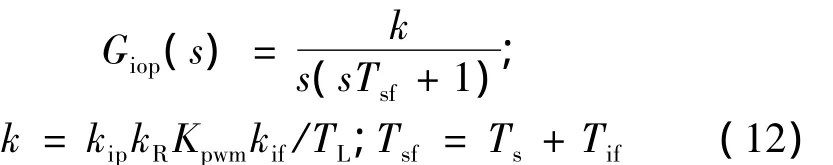
其電流內環閉環傳遞函數為:

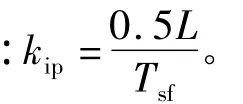
3.2 電壓外環控制器設計

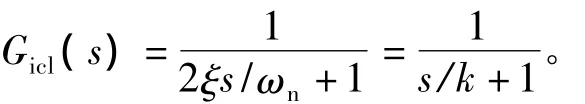
圖6 電壓外環控制器原理框圖

圖6 中，kvp、kvi表示電壓外環 PI控制器參數，kuf、Tuf分別表示電壓反饋通道比例放大系數和時間濾波常數。當忽略負載電流的外在擾動時，系統的開關傳遞函數為:

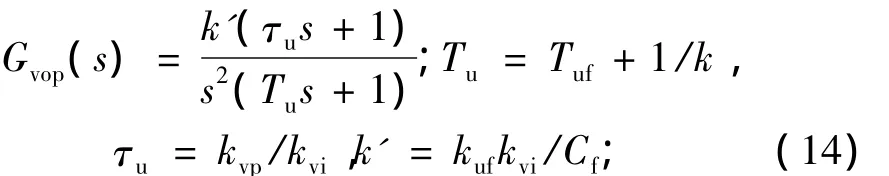
可見，電壓外環采用PI控制器后為一典型的Ⅱ型系統，其波特圖如圖7所示，可以依照工程常用的典型的Ⅱ型系統設計準則。工程中常用的設計準則有:

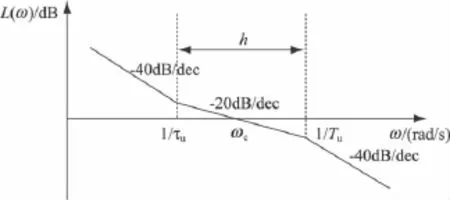
圖7 典型Ⅱ型系統波特圖

(1)Mr=Mmin準則:使得系統閉環幅頻特性的諧振峰值Mr為最小的準則。即Mr最小，使得超調量和調整時間最小。

(2)γ=γmax準則:使得系統開環頻率特性中的相位裕量γ為最大的準則。即相位裕量最大，使得超調量最小。

根據上式可先求得閉環系統的相位裕度:

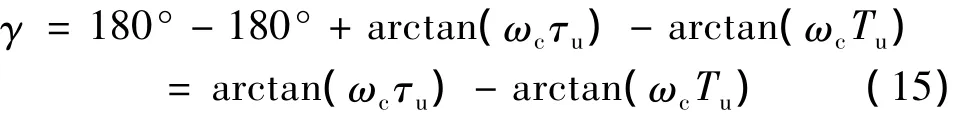
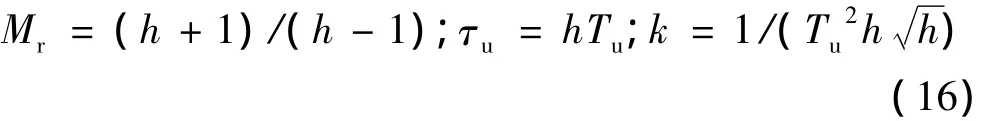
工程設計的關鍵就是確定中頻帶寬h。工程應用中，h的取值范圍通常為3～10之間。h取值越大，系統的超調量越大，系統調節時間越長，相角裕度越大，反之亦然。通常情況下，折衷選擇h為4，5時，系統調節時間較短，可獲得較好的控制性能。

3.3 諧振控制器設計

電壓外環的諧振控制器獨立于PI控制器進行設計，它只對某些特定的頻率點mωe進行控制。實際應用中的諧振控制器還需要提供一定的超前相位角φm，用以對采樣、計算以及PWM調制等過程中的延遲相位角進行補償。由于上述諧振控制器在諧振頻率點是零阻尼的，實際過程中的噪聲極易引起系統的不穩定。因而，在諧振控制器中引入阻尼系數ξm，提供足夠寬的頻率調節范圍，在增加系統阻尼的同時，使其增益下降，保證系統的穩定性。改進后的諧振控制器其數學描述形式為:

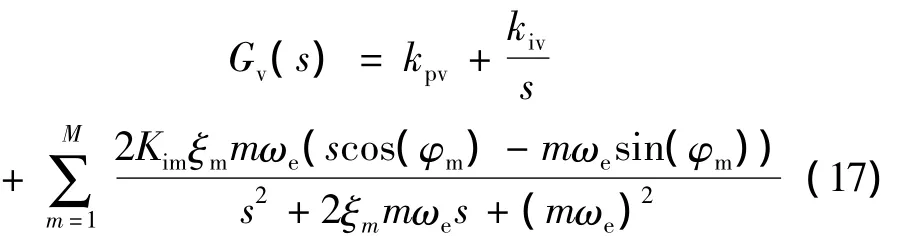
式中，m表示需控制的諧波次數;ωe表示基波頻率;Kim表示m次諧振控制器的增益。需提供的相位超前角φm計算可依據公式(18)

式中，τT表示采樣、計算以及PWM調制等過程中總的時間延遲(一般取2個采樣周期)。不難發現，隨著諧波次數增大，需要的系統延時相位角也隨之增大，這與實際情況是相吻合的。諧振控制器阻尼系數ξm的設計可依據公式(19)。?

式中，△ω表示在特定頻率點mωe的控制帶寬。為保證控制器在特定頻率點有足夠的控制帶寬和合適的增益，△ω需要隨著諧波次數的m增大也適當增大［6］。

應用諧振控制器可以獲得良好的穩態性能，但其動態性能較差。當電壓外環采用PI+R復合控制器，利用PI控制器獲得良好的動態性能，諧振控制器保證其穩態精度。以上內容以d軸控制器為例，基于自動控制系統工程化設計方法理論，詳細介紹了電流內環，電壓外環，及諧振控制器的參數設計方法。q、o軸控制器的設計方法與之類似，這里不再詳細論述，值得注意的是，o軸等效系統的電感參數不同于d、q軸;d、q軸電壓外環控制器在原有PI控制器基礎上，疊加2倍基波頻率的諧振控制器;o軸電壓外環控制器在原有PI控制器基礎上，疊加基波頻率的諧振控制器。

4 仿真結果

為驗證所述控制方案的正確性，采用Matlab/Simulink對整個三相四橋臂逆變器進行系統仿真，逆變器輸出電壓頻率為50 Hz，輸出相電壓峰值為311 V，開關頻率為16 kHz，每相濾波電感為1 mH，濾波電容為150 μF。不平衡負載情況為:A相負載電阻10 Ω(100%滿載)，B、C相空載的嚴重不平衡情況。各d、q、o軸控制器參數設計如表1所示。

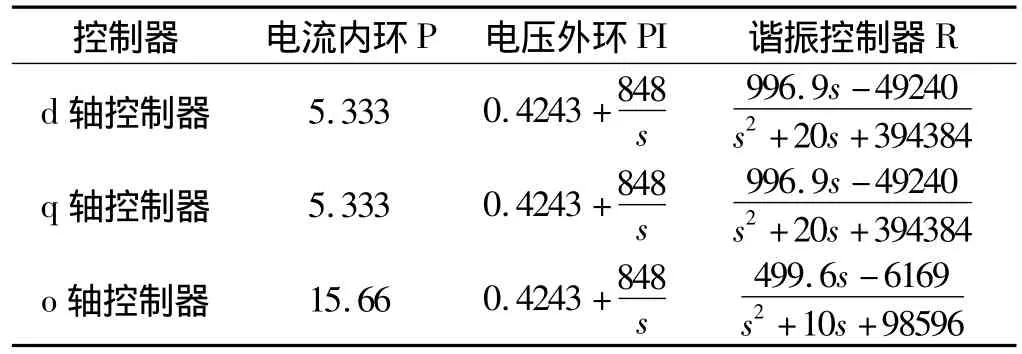
表1 d、q、o軸控制器參數

三相四橋臂逆變器采用PI-P雙閉環控制器空載正常運行，0.075 s時刻突加三相不平衡負載(A相阻性滿載，B，C相空載)，持續運行5個基本周期后，在0.175 s時刻突卸不平衡負載，系統輸出三相電壓波形如圖8所示。可見空載情況下，電壓外環采用PI控制器即可獲得良好的穩態性能。突加和突卸三相不平衡負載后，三相輸出電壓經一個基波周期后即可完全恢復，系統動態性能良好。三相輸出電壓經變換到d、q、o軸后，d、q軸包含正序電壓分量經坐標變換后得到的直流分量，以及負序電壓分量經坐標變換后得到的二次基波頻率交流量，o軸包含由零序分量經坐標變換后得到基波頻率交流量。其中d軸直流電壓分量即為三相輸出電壓正序分量峰值，二次基波頻率交流量峰值為三相電壓負序分量峰值，o軸基波頻率交流分量峰值即為三相電壓零序分量峰值。其d、q、o軸電壓分量仿真波形如圖9所示，三相外接不平衡負載時，三相不平衡電壓負序分量為7.5 V，零序分量為7 V。三相輸出電壓負序不平衡度為2.41%，零序不平衡度為2.25%。

當電壓外環在原有PI控制器基礎上添加諧振控制器后，系統采用PIR-P雙閉環控制器空載正常運行，在0.075 s突加三相不平衡負載，持續運行5個基本周期后，在0.175 s時刻突卸不平衡負載，其三相輸出電壓波形如圖10所示，其d、q、o軸的電壓分量波形如圖11所示。

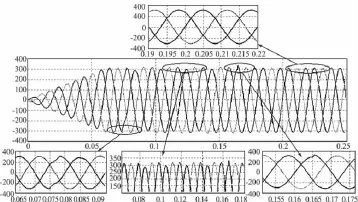
圖8 PI-P雙閉環控制器下三相輸出電壓仿真波形

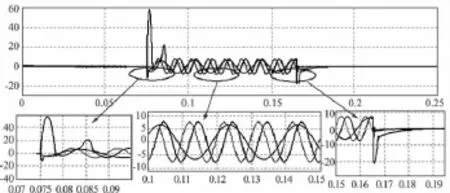
圖9 PI-P雙閉環控制器下d、q、o軸電壓分量仿真波形

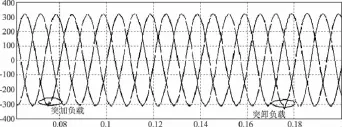
圖10 PIR-P雙閉環控制器下三相輸出電壓仿真波形

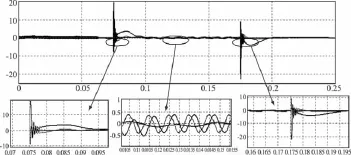
圖11 PIR-P雙閉環控制器下d，q，o軸電壓分量仿真波形

可見，諧振控制器對d、q、o軸二次和基波次交流分量抑制作用顯著。電壓外環采用諧振控制器后，三相外接嚴重不平衡負載時，負序電壓分量為0.4 V，零序電壓分量為0.1 V。三相輸出電壓負序不平衡度為0.129%，零序不平衡度為0.032%。三相輸出電壓不平衡度得到顯著減小。

5 結語

本文主要針對三相四橋臂逆變器接不平衡負載情況下，為改善三相輸出電壓不平衡度，提出一種電壓外環PI控制器與諧振控制器聯合控制的控制策略。以A相100%阻性滿載，B，C相空載這一嚴重負載不平衡情況為例，分別對電壓外環采用PI控制器和PIR控制器兩種情況作對比分析，發現諧振控制器的使用顯著改善了系統輸出電壓不平衡度。這種控制策略可應用于對三相輸出電壓對稱性要求較高的場合。

［1］孫 馳，魯軍勇，馬偉明，等.一種新的三相四橋臂逆變器控制方法［J］.電工技術學報，2007，22(2):58-64.

［2］楊 宏，阮新波，嚴仰光.采用最大電流誤差調節的四橋臂三相逆變器［J］.電力電子技術，2003，37(1):32-33.

［3］Zhang R，Boroyevich D.Three-dimensional space vector modulation for four-leg voltage source converters.IEEE Trans on PE，2002，17(3):314-320.

［4］Prats M M，Franquelo L G.Three-dimensional space vector modulation in abc coordinates for four－leg voltage source converters.IEEE Trans on PE Letters，2003，1(4):104-109.

［5］Xiong Jian，Kang Yong，Zhang Kai，et al.Comparison study of voltage space vector PWM and conventional SPWM［J］.Power Electronics，1999(1):25-28.

［6］Eyyup Demirkutlu，Ahmet M.Hava，et al.Output Voltage Control of A Four-Leg Inverter Based Three-Phase UPS by Means of Stationary Frame Resonant Filter Banks［J］.IEEE Trans on PE，2001，10(2):124-131.