對向心加速度物理意義的探討
湯家合
(南京師范大學附屬揚子中學,江蘇南京 210048)
閱讀本刊2010年第3期的文章《向心加速表示速度方向變化的快慢嗎》(以下簡稱“向文”),很受啟發,也引發了本人對相關問題的進一步思考.
“向文”給出了“物體的角速度是表示物體做圓周運動時速度方向變化快慢的物理量,向心加速度不能表示物體做圓周運動的速度方向變化的快慢”的觀點,但對向心加速的物理意義并未論及.本文想結合物理學史的有關知識和本人的一些思考,給出向心加速的物理意義,供讀者評鑒.
公元1666年,牛頓為了說明天體間的引力和地球上的物體所受的重力可能是同一種力而對此問題有所論述,下面就借此思想對該問題進行論證.
如圖1所示,設質點在大小不變的向心力作用下做勻速圓周運動,質點開始位于圓周上的 A點,速率為 v,經過一段時間 t后,到達 B點.根據運動的合成與分解的法則,實際的“圓周運動可以看作是沿
切線方向的勻速直線運動與沿法線向心方向的勻加速直線運動的合成.故物體的實際位移AB可以看作是沿切線方向的位移AC與沿法線方向的位移CB的矢量和.


圖1
由以上推導可以看出,物體做勻速圓周運動的向心加速度an就是瞬時法線方向勻加速直線運動的加速度a,它表示的是物體沿法線“落向圓心”運動時速度大小的變化快慢,是向心力作用的結果,即因此,向心加速度 an與直線運動中的加速度沒有本質的區別,它們都是描述速度大小隨時間變化快慢的物理量.在勻速圓周運動中,線速度的大小不隨時間變,而方向時刻在變,其實是物體沿圓周切向的慣性運動和物體沿半徑方向“落向圓心”的勻加速直線運動合成的結果.
一脈相承,中學物理所學的平拋運動和斜拋運動都可以進行類似的處理:如圖2,平拋運動可以看成是水平方向的勻速直線運動和豎直方向的自由落體運動的合成;如圖3,斜上拋運動可以看成是沿初速度方向的勻速直線運動和豎直方向的自由落體運動的合成.而這兩例中物體的加速度和圓周運動中的向心加速度都沒有本質的區別,均表示了速度大小的變化快慢.

圖2
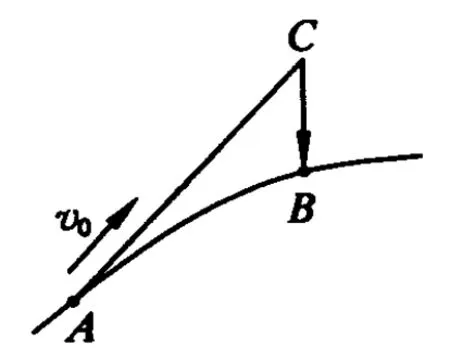
圖3
下面再進一步討論兩個與此相關的問題.
問題1:向心加速度與角速度
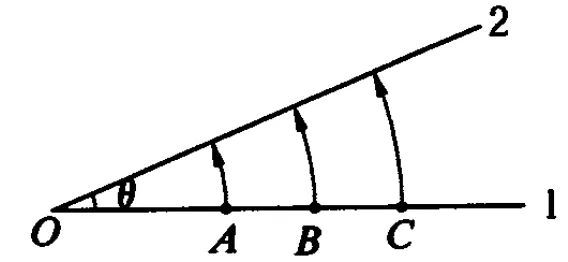
圖4
如圖4所示,位于同一桿上的質點 A、B、C具有相同的角速度,當桿從位置1勻速轉動到位置2時,3個質點速度方向的改變相同,故速度方向改變的快慢也相同,但3個質點的向心加速度并不同.這說明向心加速度確實不是描述速度方向改變快慢的物理量,而角速度才是描述速度方向變化快慢的物理量.半徑越大物體做圓周運動時所需的向心力也越大,故向心加速度越大,這說明物體沿半徑“落向圓心”運動速度的大小改變越快,并不說明速度的方向改變越快.
其實,“向心加速度表示圓周運動物體速度方向變化的快慢”這一觀點在正規的教科書中是找不到的(如高中物理、普通物理、理論物理等教材),只是在各種教輔資料中廣為流傳,故在中學階段對向心加速度概念的教學產生了負面影響.
問題2:變速圓周運動中的加速度
如圖5所示,設物體沿圓周做變速運動由 A點運動到B點,速度由 vA變為vB,所用時間為Δt.若在矢量 vB上截取長度等于vA的一段后得到矢量Δv2,它反映了速度大小的變化;而圖中的Δv1則反映了由速度的方向變化而引起的速度改變.易知Δv=Δv1+Δv2,其中Δv1為向心力所致,Δv2為物體所受合力沿切向的分力所致.
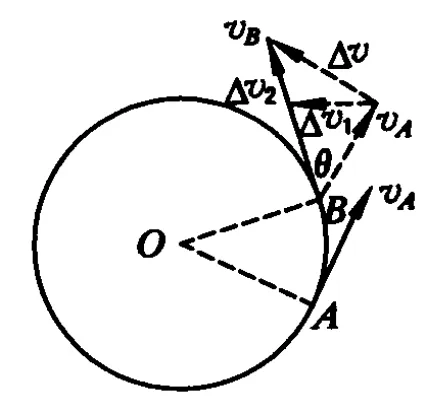
圖5
1 潘永祥,王錦藝.物理學簡史.武漢:湖北教育出版社,1990.234

