一道值得商榷的高考題

葛 洲

(南京外國語學(xué)校,江蘇南京 210008)

2010年海南高考物理試題中第5題是一道值得商榷的試題.原題如下:

如圖1,水平地面上有一楔形物塊a,其斜面上有一小物塊b,b與平行于斜面的細(xì)繩的一端相連,細(xì)繩的另一端固定在斜面上.a與b之間光滑,a和b以共同速度在地面軌道的光滑段向左運(yùn)動(dòng).當(dāng)它們剛運(yùn)行至軌道的粗糙段時(shí)

(A)繩的張力減小,b對a的正壓力減小.

(B)繩的張力增加,斜面對b的支持力增加.

(C)繩的張力減小,地面對a的支持力增加.

(D)繩的張力增加.地面對a的支持力減小.

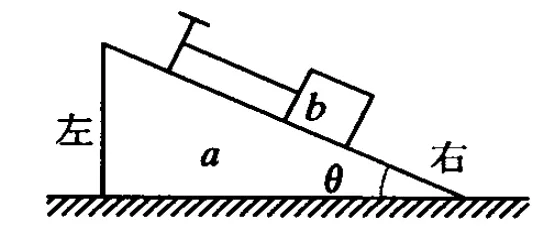
圖1

試題給出答案為(C),筆者認(rèn)為(C)選項(xiàng)僅僅是一個(gè)可能的答案,而不是一定的情況,因此本題表述有問題.

分析:設(shè)a質(zhì)量為M,b質(zhì)量為m,地面對 a的支持力為N1,繩上張力為 T,斜面對 b的支持力為N2.

(1)在光滑段運(yùn)動(dòng)時(shí),以 a、b整體為研究對象,它們共同做勻速運(yùn)動(dòng)可得N1=(M+m)g.以b為研究對象可得T=mgsinθ,N2=mgcosθ.

(2)當(dāng)它們運(yùn)動(dòng)到粗糙段時(shí),設(shè) a與地面間的動(dòng)摩擦因數(shù)為μ.

臨界狀態(tài)為繩子仍然是直的,但張力剛好減為零.以a、b整體為研究對象,a、b共同加速度a=μg,以 b為研究對象a=gtanθ,此時(shí) μ=tanθ即為臨界條件.

①μ≤tanθ時(shí),a、b一起做減速運(yùn)動(dòng),加速度為 a=μg,方向水平向右.

以a、b整體為研究對象,由豎直方向受力平衡得 N1=(M+m)g.

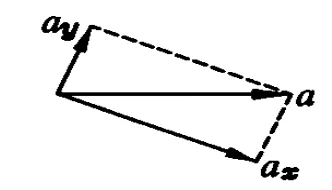
圖2

以b為研究對象,把加速度 a沿斜面方向和垂直于斜面方向分解,如圖2.應(yīng)用牛頓第二定律,沿斜面方向有

T=mgsinθ-max=mgsinθμmgcosθ,

垂直于斜面方向有

N2=mgcosθ+may=mgcosθ+μmgsinθ.

與光滑段時(shí)的T,N1,N2表達(dá)式對比得,此時(shí),T減小,N1保持不變,N2增加.

②μ＞tanθ時(shí),a將相對于b向上滑動(dòng),b物體有豎直向上的加速度分量,處于超重狀態(tài),所以 N1＞(M+m)g,定量分析可計(jì)算出 N1的大小,過程如下:

以a物體為參照物,設(shè)a物體加速度為a,b相對于a的加速度為a相,方向沿斜面向上,對 b受力分析,如圖3,其中 ma為非慣性力,應(yīng)用牛頓第二定律得

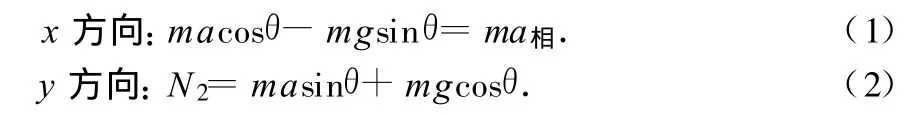
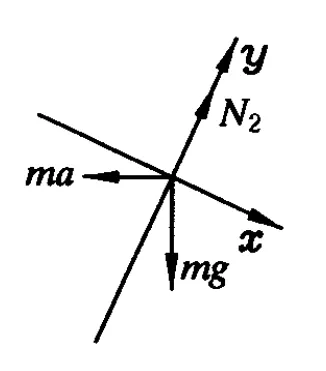
圖3

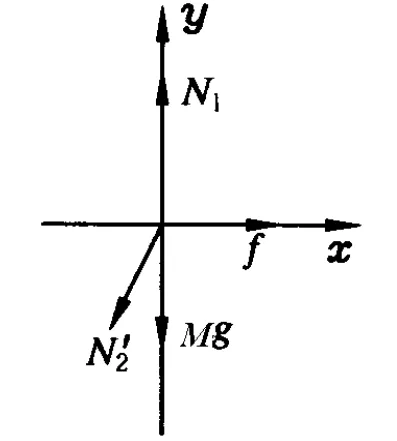
圖4

對 a受力分析,如圖4,應(yīng)用牛頓第二定律得

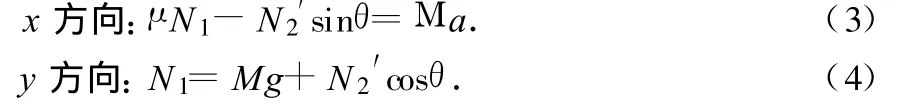
其中 N2=N2′.

由(2)～(4)式可解得

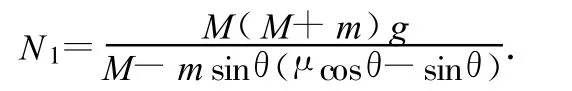
所以 μ＞tanθ時(shí),N1＞(M+m)g,與光滑段 N1表達(dá)式對比得:N1增加;把(2)式與光滑段 N2表達(dá)式對比得:N2增加;此時(shí) T=0,顯然 T減小.由(1)～(4)式可解得

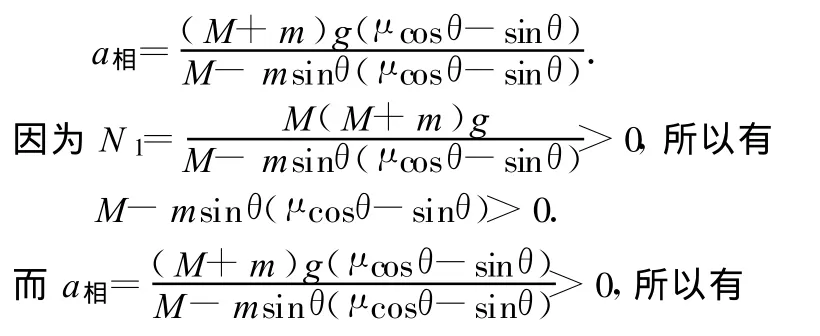
μcosθ-sinθ＞0,即μ＞tanθ,反映了μ=tanθ即為臨界狀態(tài).

綜上所述,所有選項(xiàng)都不正確.給出的標(biāo)準(zhǔn)答案為(C),其實(shí)(C)選項(xiàng)是可能出現(xiàn)的情形之一,而不是一定會(huì)出現(xiàn)的結(jié)果.當(dāng)μ≤tanθ時(shí),地面對物體a的支持力保持不變.