橢圓型彈性球鉸鏈轉動性能及疲勞強度研究

李成剛 尤晶晶 吳洪濤

南京航空航天大學，南京，210016

0 引言

在微小型設備中，對實現小范圍內偏轉的支承，不僅要求分辨率高，而且要求尺寸微型化。彈性鉸鏈符合上述要求，其中部較為薄弱，在彎矩的作用下可以產生彈性角變形，彎矩去除后又能恢復到原形。與傳統鉸鏈相比，彈性鉸鏈具有體積小、無機械摩擦、無間隙、無回退空程等優點［1］。1965年，Paros等［2］首次給出了圓弧形彈性鉸鏈的簡化計算公式。基于不同的運動精度和運動范圍，目前國內外研究的彈性鉸鏈幾何轉角結構除圓弧形外還有直梁形［3］、橢圓形［4］、拋物線形［5］、雙曲線形［6］等。

目前，彈性鉸鏈的研究方法普遍采用數值積分法和有限元方法，研究對象主要集中在單軸和雙軸轉動［7－8］。由于橫截面慣性矩、極慣性矩等幾何量的不同，單軸或雙軸彈性鉸鏈的理論推導結論對三軸彈性鉸鏈一般不適用；而球鉸鏈在科學研究以及工業生產中被使用的頻率相當高。本文系統地對橢圓形彈性球鉸鏈的柔度、精度以及疲勞強度進行理論推導和分析，旨在為彈性球鉸鏈材料的選擇以及結構參數的優化設計等提供理論依據。

1 柔度計算

柔度是評價彈性鉸鏈最重要的性能參數之一，在保證強度的前提下，通常希望鉸鏈具有大的柔度以確保較少的能量損耗。橢圓形彈性球鉸鏈的模型如圖1所示，其任一軸切面如圖2所示。其中，a、b分別為橢圓的長短半軸長；e為彈性鉸鏈中柔性部分長度的一半；t為彈性鉸鏈中厚度的最小值；θm為鉸鏈中橢圓廣角的一半；O點、B點所在的橫截面分別是鉸鏈柔性部分的起始面和終止面，將它們分別看作為固定端和自由端；球鉸鏈的轉動中心A點所在的橫截面是鉸鏈上柔性部分的最薄處。

圖1 橢圓形彈性球鉸鏈

圖2 橢圓形彈性球鉸鏈軸切面

設鉸鏈的軸線為X軸，原點選在O點。過鉸鏈上任意點P的橫截面的直徑h（φ）以及面積A（φ）、慣性矩I（φ）、極慣性矩IP（φ）可以分別表示為

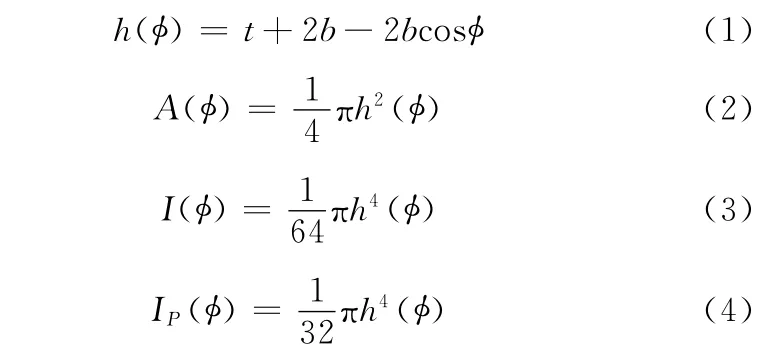
在彈性球鉸鏈的自由端作用彎矩M時，鉸鏈會發生彎曲變形，表現為橫截面繞其中性軸轉動；作用扭矩T時，鉸鏈會發生扭轉變形，表現為各橫截面之間繞鉸鏈軸線相對轉動了一個角度。為了定量地考察彈性球鉸鏈的柔度特性，定義A、B兩個橫截面在單位彎矩下的轉角差θAB表征彎曲柔度，截面B在單位扭矩下的轉角φB表征扭轉柔度。

應用卡氏第二定理，可以分別計算在彎矩M的作用下A、B截面繞其中性軸轉動的角位移θA和θB：

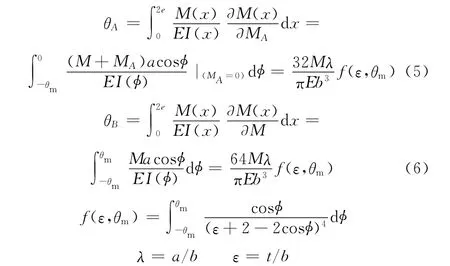
式中，E為鉸鏈材料的彈性模量；MA為在A截面虛加的彎矩。

根據定義，計算彈性球鉸鏈的彎曲柔度：

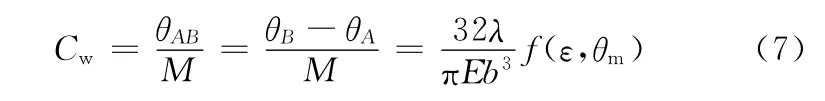
應用卡氏第二定理，求解在扭矩T作用下截面B相對于固定端的扭轉角：

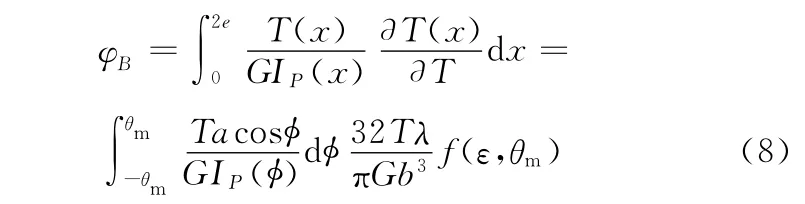
式中，G為鉸鏈材料的切變模量。

計算彈性球鉸鏈的扭轉柔度：

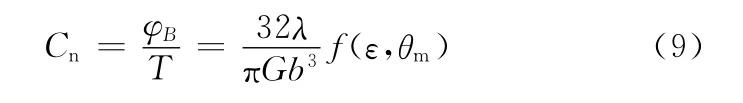
2 精度計算

由于彈性鉸鏈是通過彈性變形來實現鉸鏈運動的，施加在鉸鏈上的廣義力會導致鉸鏈中心點偏離其幾何中心，進而影響彈性鉸鏈的精度。當在鉸鏈的自由端作用彎矩M時，中心點A會產生一個撓度ωA，定義單位彎矩下的撓度為彎曲精度；當在鉸鏈的自由端作用拉力F時，中心點A會偏移一段距離ΔA，定義單位拉力下的偏移為拉伸精度。

應用卡氏第二定理，計算在彎矩M作用下A點撓度：

計算彈性球鉸鏈的彎曲精度：

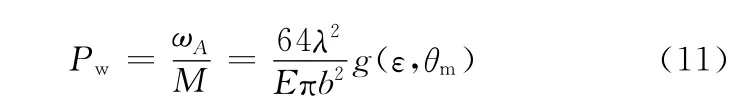
在拉力F作用下，計算A點偏移量：

3 柔度精度比

由式（7）、式（9）、式（11）、式（13）可以看出：彈性球鉸鏈的柔度和精度往往是矛盾的，很難同時保證兩個指標都高。例如，橢圓的長短半軸之比越大，則鉸鏈的柔度越大，但精度會越低。為了兼顧柔度和精度，本文提出一個全新的概念：將彈性球鉸鏈的柔度精度比作為評價彈性球鉸鏈性能的綜合指標，并記作V。定義

顯然，V值越大，表征彈性球鉸鏈的綜合性能越好。將式（7）、式（9）、式（11）、式（13）代入式（14），得到彈性球鉸鏈柔度精度比的解析表達式：

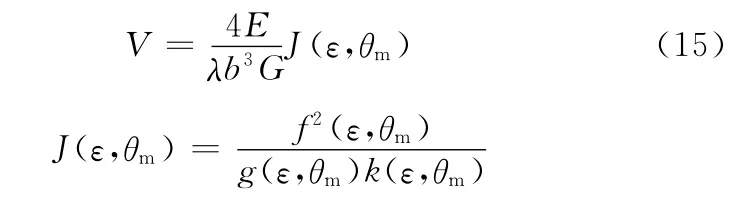
借助于Mat hematica軟件強大的符號運算以及繪圖功能，繪制二元函數J（ε，θm）的曲面圖，如圖3所示，其中，ε、J（ε，θm）均是量綱一參量。

在保證強度的前提下，根據式（15）和圖3可以分析得到，橢圓形彈性球鉸鏈的材料特性以及結構參數與其綜合性能滿足如下關系：

（1）材料的彈性模量越大、切變模量越小，則彈性球鉸鏈的綜合性能越好。

（2）橢圓長短半軸之比越小，則鉸鏈的綜合性能越好，即圓弧形彈性球鉸鏈的綜合性能比橢圓形的綜合性能好。

（3）鉸鏈最小厚度與橢圓短半軸之比越大，則其綜合性能越差；但當此比例大于0．8時，最小厚度對球鉸鏈性能的影響不再明顯。

（4）鉸鏈的廣角越大，則其綜合性能越差；但當廣角大于2．5rad（即θm＞1．25rad）時，其對球鉸鏈性能的影響不再明顯。

（5）彈性球鉸鏈的幾何尺寸越小，則其綜合性能越好。

圖3 二元函數J（ε，θm）的曲面圖

4 疲勞強度校驗

上文通過理論推導，在滿足強度的前提下，得到了關于橢圓形彈性球鉸鏈優化設計的5個結論。然而，彈性球鉸鏈通常工作于交變應力環境下，為了使其不發生疲勞破壞，有必要推導出鉸鏈疲勞強度的校驗公式。顯然，鉸鏈的危險截面是厚度最小的橫截面A。在自由端同時作用彎矩M、拉力F和扭矩T時，危險截面上距離中性軸最遠處的應力值最大，其最大正應力σmax和最大切應力τmax分別為

根據第三強度理論以及疲勞強度的經驗公式［9］，可以推導出在同步的拉彎扭組合對稱循環交變應力作用下彈性球鉸的疲勞強度校驗公式：

式中，nστ、nσ、nτ分別為彈 性 鉸 鏈在組合 交 變 應力、正應力、切應力下的工作安全系數；n為人為規定的彈性鉸鏈工作安全系數；σ－1、τ－1分別為正應力和切應力的疲勞極限；kσ、kτ分別為應力集中對正應力和切應力的影響系數；εσ、ετ分別為彈性鉸鏈的幾何尺寸對正應力和切應力的影響系數，β為材料表面加工的影響系數。

由式（16）～式（18），可以計算得到彈性球鉸鏈疲勞強度的校驗公式：

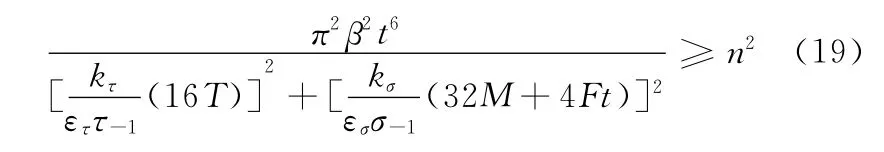
施加在彈性球鉸鏈自由端的廣義力、鉸鏈的材料特性、最小厚度以及加工工藝等滿足不等式（19）時，鉸鏈才能夠經受至少107次交變載荷的作用而不產生斷裂現象。可見，在設計彈性球鉸鏈時不能只是一味地追求柔度、精度等性能，而不考慮其疲勞強度。

5 應用實例

為了使彈性球鉸鏈具有良好的轉動性能，依據第3節最后所得到的第一個結論，設計時應選用彈性模量大而切變模量小的材料。在產品的設計階段，除了材料的選擇之外，設計人員還面臨一個合理確定各尺寸參數的難題。例如，在設計橢圓形彈性球鉸鏈時，有幾組尺寸參數可供選擇，表1列出了其中的4組選擇方案。

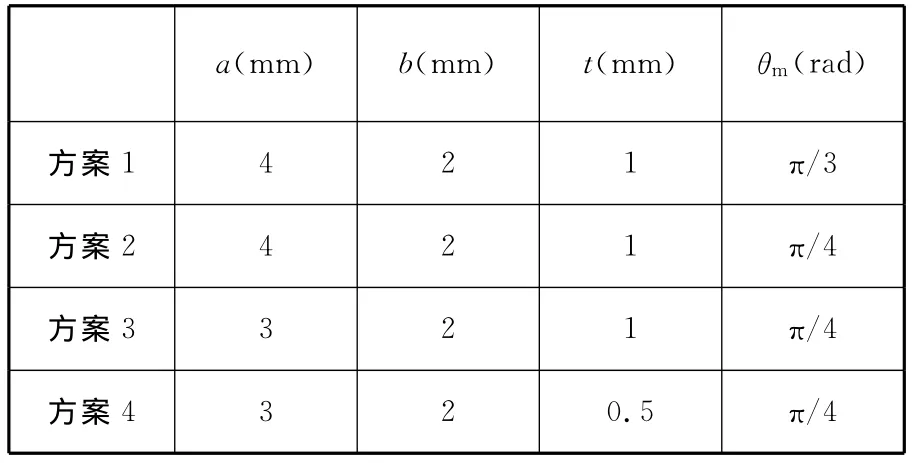
表1 橢圓形彈性球鉸鏈尺寸參數的選擇方案

依據第3節最后所得到的后4個結論，可以對表1中的4組方案做出優劣判斷，其中，方案4的彈性球鉸鏈的轉動性能最優。確定尺寸參數之后，再根據鉸鏈的材料特性、表面加工處理工藝、作用在鉸鏈上的載荷以及不等式（19）對彈性球鉸鏈的疲勞強度進行校驗。如果不等式成立，則該方案滿足設計要求；否則，應增大最小厚度t，直到不等式（19）成立為止。這樣，設計出來的橢圓形彈性球鉸鏈一定是最優的。

6 結束語

本文系統地研究了橢圓形彈性球鉸鏈的轉動能力和轉動精度，以力學卡氏第二定理為理論基礎，通過引入中間變量，并將橢圓的離心角作為積分變量，推導出彈性球鉸鏈彎曲柔度、扭轉柔度、彎曲精度以及拉伸精度的解析表達式。提出彈性球鉸鏈柔度精度比的概念，給出了其定義表達式，并以此作為評價彈性鉸鏈綜合性能的指標；通過計算得到了在滿足強度的前提下提高該指標的措施，即鉸鏈應選用彈性模量大、切變模量小的材料；橢圓廣角、橢圓長短半軸之比以及鉸鏈最小厚度與橢圓短半軸之比都應盡可能小。推導了彈性球鉸鏈疲勞強度的校驗公式，用于檢驗設計出的鉸鏈能否滿足工作需求。最后，通過一個應用實例介紹了彈性球鉸鏈的詳細設計過程。

［1］ Yeh H C，Ni W T，Pan S S．Digital Closed－loop Nanopositioning Using Rectilinear Flexure Stage and Laser Interfer o metry［J］．Contr ol Engineering Practice，2005，13：559－566．

［2］ Paros J M，Weisboro L．How to Design Flexure Hinges［J］．Machine Design，1965，37：151－157．

［3］ 秦宇，馮之敬．直梁型柔性鉸鏈制造誤差對剛度性能影響的建模與分析［J］．中國機械工程，2008，19（18）：2182－2185．

［4］ 陳貴敏，韓琪．深切口橢圓柔性鉸鏈［J］．光學精密工程，2009，17（3）：570－575．

［5］ Nicolae L，Jeffrey S N，Ed ward O M，et al．Parabolic and Hyper bolic Flexure Hinges：Flexibility，Motion Precision and Stress Characterization Based on Co mpliance Closed－for m Equations［J］．Precision Engineering，2002，26：183－192．

［6］ Nicolae L，Jeffrey S N，Ephrahim G．Design of Sy mmetric Conic－section Flexure Hinges Based on Closed－for m Compliance Equations［J］．Mechanism and Machine Theory，2002，37：477－498．

［7］ 吳鷹飛，周兆英．柔性鉸鏈轉動剛度計算公式的推導［J］．儀器儀表學報，2004，25（1）：125－128．

［8］ Awtar S，Slocu m A H，Sevincer E．Characteristics of Beam－based Flexure Modules［J］．ASME Journal of Mechanical Design，2007，129（6）：625－639．

［9］ 戴少度．材料力學［M］．北京：國防工業出版社，2000．