基于反演理論在役連續剛構橋有效預應力識別＊

張兆寧，賀拴海，趙 煜

(1.長安大學 公路學院，陜西西安 710064;2.蘭州理工大學土木工程學院，甘肅蘭州 730050)

基于反演理論在役連續剛構橋有效預應力識別＊

張兆寧1，2，賀拴海1，趙 煜1

(1.長安大學 公路學院，陜西西安 710064;2.蘭州理工大學土木工程學院，甘肅蘭州 730050)

由于受環境、氣候、荷載及其他外在因素的共同影響，施加于橋梁結構的預應力也隨之發生變化，準確掌握其內部真實的應力狀態對保證橋梁的安全運營至關重要。針對這一問題，以反演理論為基礎，依據橋梁服役期間結構變位的實際監測結果，由位移反分析法得到了不同時間點梁體內存在的有效預應力數值。以某一預應力混凝土連續剛構橋為例，通過反分析得到的有效預應力為參數，重新建立有限元計算模型，分析了在設計荷載作用下梁體強度及剛度的變化情況。理論結果與實測位移的對比表明，利用反分析法可以較為精確地預測服役期間橋梁內真實的預應力狀態。

連續剛構橋;反演理論;目標函數;有效預應力;識別

對已建預應力混凝土梁橋而言，在服役期間由于受到外界不同因素(如荷載、氣候、自然災害等)的共同影響，其原始強度、剛度狀態均會產生相應的變化，其表現主要是位移、應力的不斷增大。伴隨位移場、應力場的不斷擴散，梁體一些部位會出現不同程度的開裂損傷等問題，直接影響橋梁的使用性、耐久性及可靠性。為此，國內外學者通過對影響梁體強度、剛度的主要因素的分析研究表明，其中，預應力損失是引起預應力結構受力性能隨時間逐漸退化的主要因素之一。目前，對引起預應力損失的成因、組成、解決措施等相關理論研究均比較深入［1－6］。但國內外在成橋狀態至不同運營期間梁體實際有效預應力狀態方面的相關研究還比較少，如何準確預測及實測出梁體有效預應力仍然是需要深入研究的一個課題。國內規范給出了各種預應力損失的理論計算公式［7］，但對在役預應力混凝土梁橋而言，規范中所提供的計算公式已不能再簡單地加以套用。如何確定橋梁運營期間其內部真實預應力狀態是亟待解決的一個工程難題。針對這一問題，本文以反演理論為基礎，通過實測服役期間橋梁梁體不同時間點主要控制截面測點位移，通過建立相關反分析模型對有效預應力進行了識別，然后依據反演所得結果重新建立分析模型進行正分析，以此來評價在役預應力混凝土橋梁強度及剛度的變化過程。

1 反演基本原理

參數反演問題實際上是一個目標函數的優化問題，它直接利用正分析的過程，通過迭代最小誤差函數，逐次修正未知參數的試算值，直至獲得最優解［8－11］。將模型輸出表示成待求參數的顯函數，通過模型輸出的量測值，利用函數關系反求出待求參數。對于線彈性問題中，在待求量與量測信息之間建立如下的線形方程組:

式中:［K］為未知量的影響系數陣;{x}為待求未知量陣;{y}為與量測信息有關的已知列陣。

設獨立量測信息的總數N，待求未知量總數M，量測信息的最佳估計量Ui與量測值之間的誤差為 εi，則有:

由此可知，當量測信息的總數大于待求未知量總數，即N＞M時，可將目標函數定義為:

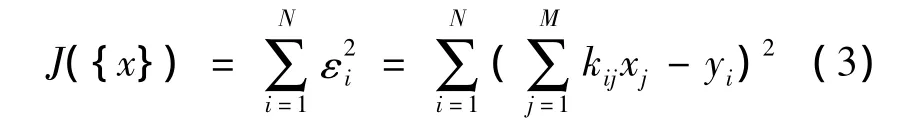
為使目標函數即最佳估計量之間誤差的平方和為最小，需要滿足的條件為:

將式(4)代入式(3)，利用最小二乘法原理作優化處理后，展開得到其正則方程基本表達式及矩陣形式:

由式(6)可解得直接用于求解材料特性參數的線形代數方程組的普遍表達式:

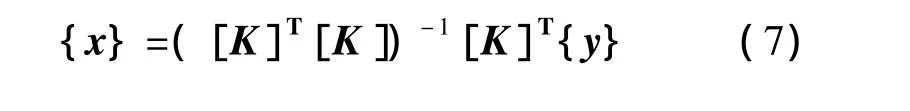
2 有效預應力反演識別

2.1 目標函數的建立

由于受環境、儀器設備、方法、讀數誤差等因素的綜合影響，現場實測的梁體位移不可避免地存在誤差。為了減小誤差，量測的數量必須大于待求參數個數，然后通過優化技術得到最優參數值。目標函數的建立是優化反分析的基礎，一般表示為系統的實際量測值和模型輸出值偏差的某個函數。在預應力混凝土梁橋預應力識別過程中可采用最小二乘法建立如下的目標函數式:

式中:n為梁體實測位移數量;ui為梁體豎向位移實測值;vi為梁體豎向位移理論計算值。

2.2 預應力辨識參數

建立反分析模型以連續介質為基礎，鋼絞線可以看做是均勻連續非線性介質，其工作狀態處于彈塑性范圍。由于梁體預應力布置時存在平彎、豎彎及橫彎情況，加之梁體構造上的差異，不同梁段處實際預應力損失也有所區別。為了簡化分析，假定同一束鋼絞線各個位置產生的預應力損失為一恒定值，該值綜合體現各項預應力損失的共同影響。對于從整體上分析預應力損失，這種簡化是可行的。因此，反分析所得的有效預應力其實為“平均綜合有效預應力”，是一個宏觀的整體性參數。

2.3 反演計算模型及參數

某一三跨預應力混凝土連續剛構橋(35.0 m+60.0 m+35.0 m)，設計標準為公路 － Ⅰ級，截面形式為單箱單室，主梁混凝土標號為C50，預應力鋼筋采用 15.24 mm鋼絞線，設計強度1 860 MPa。根據設計資料及施工期間預應力張拉控制規定，有限元分析時初始預應力輸入參數取為1 395 MPa。由于梁體位移在運營期間表現為一隨機動態變量，為此，通過布設于箱梁1/4中跨、3/8中跨及1/2中跨底板等測點的位移傳感器來量測車輛隨機通過時的動態位移。然后，將所測位移進行數理統計處理得到各測點平均效應值。為了減少溫度對實測結果的影響，測試安排在清晨進行。用于反演計算所需梁體服役期間不同時間點箱梁實測豎向位移如表1所示。對應于式(1～7)，{x}為箱梁實際有效預應力值;{y}為梁體實測位移值。反演計算有限元1/2模型如圖1所示。

圖1 有限元計算模型Fig.1 Finite element model

表1 箱梁測點豎向位移Table 1 Vertical monitoring deflection of box girder mm

2.4有效預應力反演結果

以ANSYS分析軟件為計算平臺，以不同時間點實測位移進行反演計算，梁體內有效預應力迭代隨次數的變化規律如圖2～圖7所示。

圖2 有效預應力反演迭代變化曲線Fig.2 Inversion iterative chart of effective pre－stress

圖3 有效預應力隨迭代次數的變化規律Fig.3 Inversion iterative chart of effective pre－stress

圖4 有效預應力隨迭代次數的變化規律Fig.4 Inversion iterative chart of effective pre－stress

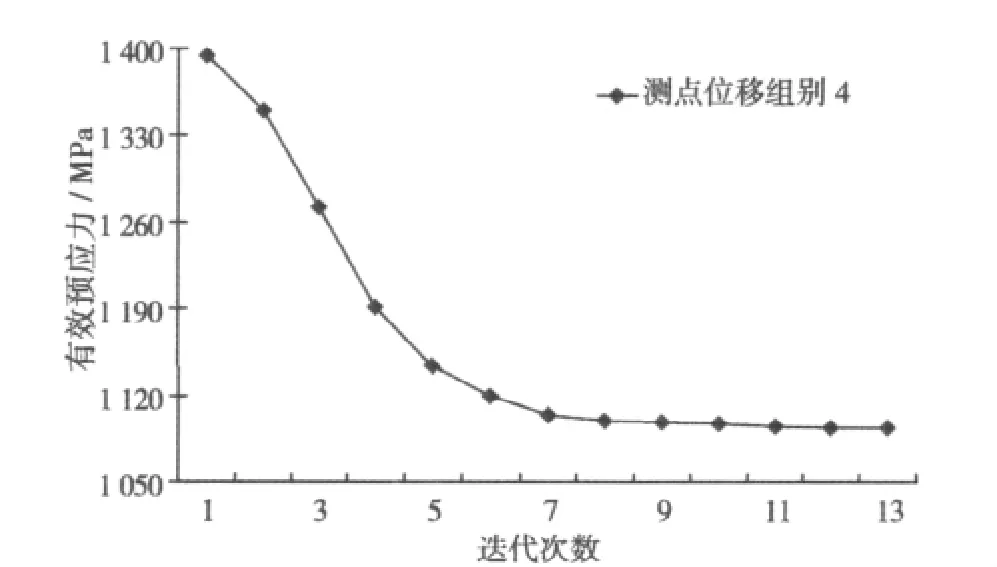
圖5 有效預應力隨迭代次數的變化規律Fig.5 Inversion iterative chart of effective pre－stress

通過分析計算可知，當中跨跨中實測豎向位移分別為 34.1，36.9，38.8，40.8，44.3 和 46.6 mm時，通過反演分析得到梁體在不同位移下對應的有效 預 應 力 分 別 為 1 261.0，1 191.2，1 144.1，1 094.3 ，1 008.1和 950.4 MPa。對應于上述各種情況下的預應力損失分別為 9.6%，14.6%，18.0%，21.6%，27.7%及 31.9%。

圖6 有效預應力隨迭代次數的變化規律Fig.6 Inversion iterative chart of effective pre－stress

圖7 有效預應力隨迭代次數的變化規律Fig.7 Inversion iterative chart of effective pre－stress

3 箱梁強度及剛度分析

以上述反演分析得到的有效預應力為參數，重新建立有限元計算模型進行強度及剛度分析，中跨跨徑撓度及底板拉應力隨不同預應力的變化曲線如圖8～圖9所示。

圖8 中跨跨徑撓度隨有效預應力的變化規律Fig.8 Deflection of mid － span with different effective pre－stress

圖9 中跨跨徑底板拉應力隨有效預應力的變化規律Fig.9 Tensile stress of bottom slab for mid － span with different effective pre－stress

通過計算可知，當施加于梁體的有效預應力分別為 90.4%，85.4%，82.0%，78.4%，72.3% 及68.1%時，中跨跨中產生的最大豎向位移分別為32.8，35.1，37.2，39.0，42.9 及 44.9 mm，實測位移與理論分析值最大誤差為4.9%。在不同的有效應力作用下，中跨跨徑底板最大拉應力分別為1.91，2.05，2.17，2.37，2.52 及 2.63 MPa。

4 結語

以反演理論為基礎，通過建立反分析模型，以預應力混凝土箱梁服役期間控制截面實測位移進行位移反分析，計算得到其運營期間不同時間有效預應力值。利用由反演分析所得的數值作為正分析計算時的初始參數，對梁體強度及剛度進行了分析，以此來動態跟蹤其應力、位移狀態。本文提出的預應力反分析法為在役預應力混凝土梁橋預應力損失識別提供了一條新的思路，可為其承載能力評估提供可靠的參數，以此確保理論分析結果的可靠性及準確性。

［1］任茶仙，竺潤祥.連續曲線箱梁預應力效應分析［J］.工程力學，2000，17(4):138 －144.

REN Cha-xian，ZHU Run-xiang.Analysis of prestressing effect for curved continuous box girders［J］.Engineering Mechanics，2000，17(4):138 －144.

［2］張元海，劉世忠.后張法預應力混凝土梁鋼束預應力損失研究［J］.中國公路學報，2002，15(2):76 －78.

ZHANG Yuan-hai，LIU Shi-zhong.Study of the loss of pre－stress of tendon in post－tensioned prestressed concrete beams［J］.China Journal of Highway and Transport，2002，15(2):76 －78.

［3］程壽山，李興慶，于剛勤，等.預應力連續梁橋預應力損失預測及測試方法研究［J］.公路交通科技，2006，23(4):71－73.

CHENG Shou-shan，LI Xing-qing，YU Gang-qin，et al.Research on predication and test method to prestressed a concrete continuous beam bridge［J］.Journal of Highway and Transportation Research and Development，2006，23(4):71－73.

［4］汪勁豐，項貽強，徐 興.大跨度混凝土橋梁預應力空間效應分析［J］.浙江大學學報，2005，39(1):154－159.

WANG Jin-feng，XIANG Yi-qiang，XU Xing.Research on spatial effect of prestressing force in long－span concrete bridge［J］.Journal of Zhejiang University:Engineering Science，2005，39(1):154 －159.

［5］汪勁豐，項貽強，徐 興.橋梁空間分析中預應力效應分析方法研究［J］.計算力學學報，2007，24(4):459 －463.

WANG Jin-feng，XIANG Yi-qiang，XU Xing.Numerical simulation of failure process of reinforced concrete specimen under uniaxial tension［J］.Chinese Journal of Computational Mechanics，2007，24(4):459 －463.

［6］李清富，辛保兵，李 科.基于SVM的預應力混凝土梁有效預應力識別［J］.鄭州大學學報，2011，32(1):18－21.

LI Qing-fu，XIN Bao-bing，LI Ke.Identification of the effective pre－stress in prestressed concrete beam based on support vector machine［J］.Journal of Zhengzhou University:Engineering Science，2011，32(1):18 －21.

［7］JTG D62—2004，公路鋼筋混凝土及預應力混凝土橋涵設計規范［S］.北京:人民交通出版社社，2004.

JTG D62—2004，Code for design of highway reinforced concrete and prestressed concrete bridges and culverts［S］.Beijin:China Communications Press，2004.

［8］袁 勇，孫 鈞.巖體工程優化反演的目標函數［J］.巖土工程學報，1994，16(2):29 －36.

YUAN Yong，SUN Jun.Objective function in optimal back analysis for rock engineering ［J］.Chinese Journal of Geotechnical Engineering，1994，16(2):29 －36.

［9］張路青，賈正雪.彈性位移反分析對地應力、彈模的反演唯一性［J］.巖土工程學報，2001，23(2):172 －177.

ZHANG Lu-qing，JIA Zheng-xue.Inversion uniqueness of elastic displacement back－analysis for ground stress，elastic modulus and poisson’s ratio［J］.Chinese Journal of Geotechnical Engineering，2001，23(2):172 －177.

［10］趙 冰，盛國剛，李 寧.位移反分析的有限元線法及其工程應用［J］.巖石力學與工程學報，2004，23(7):1146－1149.

ZHAO Bing，SHENG Guo-gang，LI Ning.Back analysis method based on finite element method of lines and its application to geo － engineering［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(7):1146 －1149.

［11］孫學先，張 慧.反演理論在懸臂灌筑平彎梁橋線形監控中的應用［J］.工程力學，2007，24(12):135－138.

SUN Xue-xian，ZHANG Hui.Appliance of inversion theory in alignment control of plane curved bridge by cantilever segmental construction［J］.Engineering Mechanics，2007，24(12):135 －138.

Effective pre－stress identification of the continuous rigid frame bridge in service based on inversion theory

ZHANG Zhao-ning1，2，HE Shuan-hai1，ZHAO Yu1

(1.School of Highway，Chang’an University，Xi’an 710064，China;2.School of Civil Engineering，Lanzhou University of Technology，Lanzhou 730050，China)

Due to the environment，climate，loads and other external factors，the pre － stress applied to the bridge is not constant.It is important for engineers to find out the accurate stress condition in order to ensure security of the bridge in service.To solve the problem mentioned above，according to actual monitoring displacement of the bridge in service at different time，the effective pre－stress is obtained by the displacement inversion method based on the inversion theory.Lastly，taking the pre－stressed concrete continuous rigid frame bridge for example，the finite element model with different effective pre－stress is established and the strength and stiffness are analyzed under design load.It is shown from the comparison results of analytical displacements and measured ones that the inverse method is an effective way to predict reasonable pre－stress for the bridge in service.

continuous rigid frame bridge;inversion theory;object function;effective pre－stress;identification

TU448.23

A

1672－7029(2011)06－0012－05

2011－11－16

國家自然科學基金資助項目(50908017)

張兆寧(1978－)，男，寧夏固原人，講師，博士研究生，從事橋梁結構評價及可靠度研究