無刷雙饋風(fēng)力發(fā)電機(jī)的H∞控制
蔡超豪
(沈陽(yáng)工程學(xué)院,遼寧沈陽(yáng) 110136)
0 引言
能源、環(huán)境是當(dāng)今人類生存和發(fā)展所要解決的緊迫問題。風(fēng)力發(fā)電是一種無污染的綠色電力,由于無刷雙饋風(fēng)力發(fā)電機(jī)的特殊結(jié)構(gòu),降低了維護(hù)費(fèi)用,提高了運(yùn)行的可靠性,已成為風(fēng)力發(fā)電研究的主要方向。
無刷雙饋風(fēng)力發(fā)電機(jī)運(yùn)行于不同風(fēng)速時(shí)有著不同的控制目標(biāo):當(dāng)其運(yùn)行于額定風(fēng)速以上時(shí),要求保持輸出功率平穩(wěn);運(yùn)行于額定風(fēng)速附近時(shí),要求保持轉(zhuǎn)速穩(wěn)定,實(shí)現(xiàn)恒轉(zhuǎn)速運(yùn)行;運(yùn)行于額定風(fēng)速以下時(shí),要求實(shí)現(xiàn)最大風(fēng)能捕獲。由于氣動(dòng)性能的影響,無刷雙饋風(fēng)力發(fā)電機(jī)具有較強(qiáng)的非線性,此外,其轉(zhuǎn)動(dòng)慣量大、工作風(fēng)速范圍寬、發(fā)電機(jī)溫度和轉(zhuǎn)軸機(jī)械阻尼不斷變化,數(shù)學(xué)模型復(fù)雜,因而實(shí)現(xiàn)精確控制較為困難。目前國(guó)內(nèi)已發(fā)表的文獻(xiàn)中有自抗擾功率解耦控制[1]、有功和無功功率控制[2]、最大風(fēng)能追蹤控制[3]、滑模變結(jié)構(gòu)控制[4]、模糊控制[5]等,都取得了一定效果,但引入先進(jìn)控制理論的文章還不多。H∞控制理論在系統(tǒng)建模和控制器設(shè)計(jì)過程中考慮了不確定性對(duì)系統(tǒng)的影響,利用解析方法設(shè)計(jì)控制器,能夠使所有被控對(duì)象均能滿足期望的性能指標(biāo),因此本文著力分析無刷雙饋風(fēng)力發(fā)電機(jī)全風(fēng)速范圍的H∞控制。
本文介紹了以下三部分內(nèi)容:(1)利用基于等效旋轉(zhuǎn)控制繞組的矢量控制模型,應(yīng)用直接反饋線性化構(gòu)建魯棒控制模型,將線性化后估計(jì)出的非線性項(xiàng)的上界作為不確定項(xiàng)處理;(2)按H∞魯棒控制理論,采用MATLAB工具箱進(jìn)行求解,得出具備參數(shù)攝動(dòng)魯棒鎮(zhèn)定性能和干擾抑制性能的最優(yōu)控制器;(3)用實(shí)例和仿真驗(yàn)證該控制算法的有效性。
1 無刷雙饋風(fēng)力發(fā)電機(jī)簡(jiǎn)介
無刷雙饋風(fēng)力發(fā)電機(jī)的基本結(jié)構(gòu)如圖1所示,定子側(cè)安裝兩套三相繞組:一套為功率繞組,磁極對(duì)數(shù)為pp,直接接工頻電網(wǎng);另一套為控制繞組,磁極對(duì)數(shù)為pc,通過變頻器接電網(wǎng)。采用自行閉合的籠形轉(zhuǎn)子或磁阻轉(zhuǎn)子,無電刷和滑環(huán)。
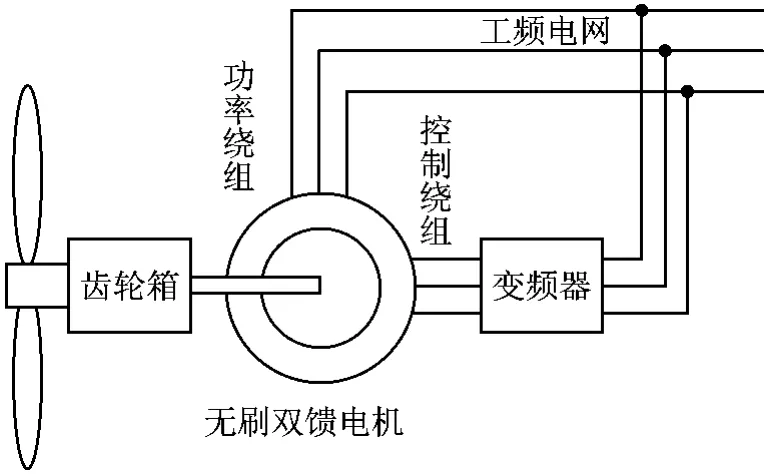
圖1 無刷雙饋風(fēng)力發(fā)電機(jī)簡(jiǎn)圖
無刷雙饋風(fēng)力發(fā)電機(jī)的頻率與轉(zhuǎn)速之間存在以下關(guān)系:
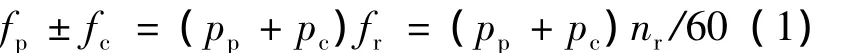
式中:fp、fc分別為功率繞組、控制繞組的電流頻率,當(dāng)繞組的相序相反時(shí)取正號(hào),反之取負(fù)號(hào);fr為發(fā)電機(jī)轉(zhuǎn)子機(jī)械頻率(fr=nr/60),轉(zhuǎn)子磁極對(duì)數(shù)為np=pp+pc,在不同風(fēng)速下發(fā)電機(jī)機(jī)械轉(zhuǎn)速nr變化時(shí),只要適當(dāng)調(diào)節(jié)控制繞組輸入電流的頻率,即可使功率繞組輸出電流的頻率維持不變。
通過變頻器調(diào)節(jié)控制繞組的電流頻率及幅值,便可控制功率繞組的電壓及頻率,進(jìn)行異步起動(dòng);并網(wǎng)后,通過調(diào)節(jié)控制繞組輸入電流的幅值和相位,即可控制功率繞組輸出的有功功率和無功功率,達(dá)到穩(wěn)頻穩(wěn)壓。變頻器容量只是電機(jī)容量的一部分,降低了成本。
2 無刷雙饋風(fēng)力發(fā)電機(jī)系統(tǒng)的矢量控制方程組
2.1 基于等效旋轉(zhuǎn)控制繞組的電壓方程
利用沈陽(yáng)工業(yè)大學(xué)王風(fēng)翔、張風(fēng)閣、王正等提出的基于等效旋轉(zhuǎn)控制繞組磁場(chǎng)定向矢量控制的數(shù)學(xué)模型[5-6],將其磁鏈方程代入電壓方程,經(jīng)過整理得出式(2):
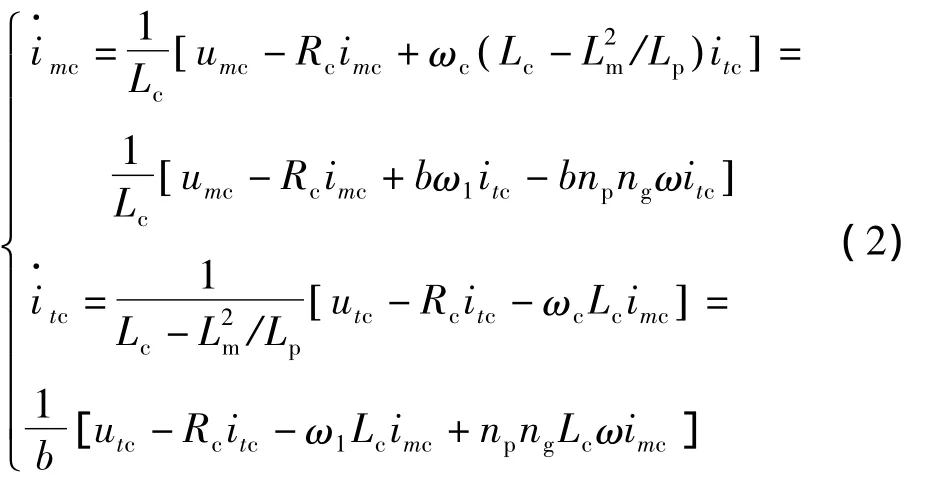
其中:u,i——電壓和電流,其下標(biāo)第1個(gè)字母代表m、t軸分量,第2個(gè)字母p、c代表功率繞組、控制繞組;
Rp,Rc——繞組的電阻;
Lp,Lc,Lm——繞組的自感及互感;
b=Lc-L/Lp;
ωp,ωc——繞組的電流角頻率;
ω1——電網(wǎng)電壓角頻率;
ωr,ω——發(fā)電機(jī)、風(fēng)力機(jī)機(jī)械角頻率;
ng——齒輪箱增速比,ng= ωr/ω。
并網(wǎng)運(yùn)行時(shí),ωp=ω1,ωc=ωp-npωr=ω1-npngω。
2.2 轉(zhuǎn)子運(yùn)動(dòng)方程
式(3)為折算到風(fēng)力機(jī)側(cè)的轉(zhuǎn)子運(yùn)動(dòng)方程[7]:
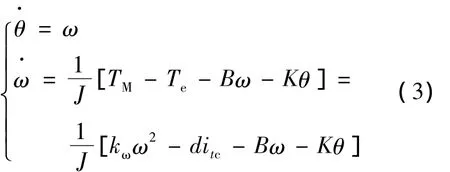
式中:TM——風(fēng)能轉(zhuǎn)換為輪轂上的機(jī)械轉(zhuǎn)矩。
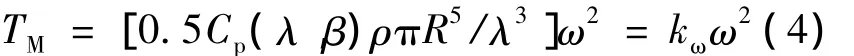
其中:kω=0.5Cp(λ,β)ρπR5/λ3;
ρ——空氣密度;
R——風(fēng)力機(jī)槳葉半徑;
Cp(λ,β)——風(fēng)力機(jī)的風(fēng)能利用系數(shù);
β——槳距角;
λ——葉尖速比,λ =ωR/υ;
υ——風(fēng)速。
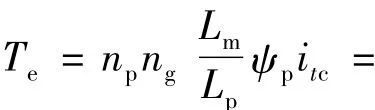
2.3 風(fēng)力發(fā)電系統(tǒng)的整體方程組
式(2)、式(3)合并為無刷雙饋型風(fēng)力發(fā)電系統(tǒng)的狀態(tài)方程,它是一組非線性、強(qiáng)耦合方程組,狀態(tài)變量為 x=[θ ω imcitc]T,控制變量為[umcutc]T。目的是:利用式(2)、式(3)設(shè)計(jì)一個(gè)具備參數(shù)攝動(dòng)鎮(zhèn)定性能和干擾抑制性能的H∞魯棒控制器,使得并網(wǎng)后的風(fēng)力發(fā)電系統(tǒng)在不確定參數(shù)和不同風(fēng)速作用下,保證風(fēng)力機(jī)控制繞組電流勵(lì)磁分量imc、轉(zhuǎn)矩分量itc和有功功率仍能按預(yù)期的軌跡運(yùn)行,以滿足最大風(fēng)能捕獲和輸出恒頻恒壓電能的要求。
3 直接反饋線性化
直接反饋線性化是中國(guó)學(xué)者提出并發(fā)展起來的基于系統(tǒng)輸入-輸出描述的一種反饋線性化方法[8],可將非線性系統(tǒng)在全局范圍內(nèi)進(jìn)行線性化處理[9-10]。與基于微分幾何理論的線性化方法對(duì)比,采用了不同的描述方式和處理方法,得到相同的線性化效果。直接反饋線性化的優(yōu)點(diǎn)是所用的數(shù)學(xué)工具簡(jiǎn)單、物理概念清晰,適合于工程應(yīng)用。
對(duì)式(2)、式(3)進(jìn)行坐標(biāo)變換,采用狀態(tài)變量的偏差量為輸出變量,得出輸出方程:
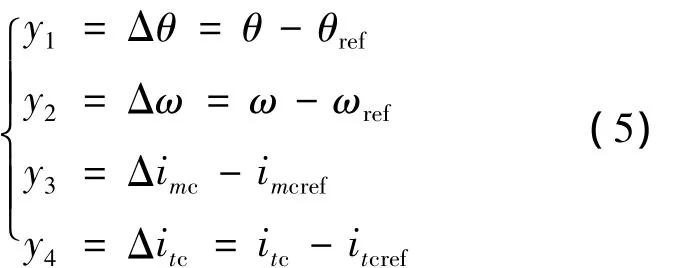
式中:θref,ωref,imcref,itcref為選定的參考值。將式(5)對(duì)t求導(dǎo)得:
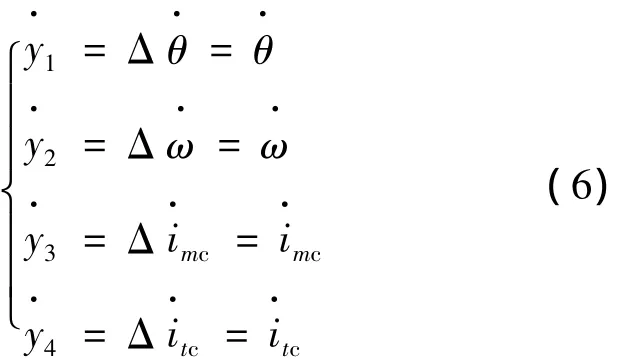
將不確定參數(shù)Rc,B,K用標(biāo)稱值和偏差值之和表示(溫度變化引起Rc的偏差,轉(zhuǎn)速變化和轉(zhuǎn)軸的柔性變化引起B(yǎng),K的偏差):
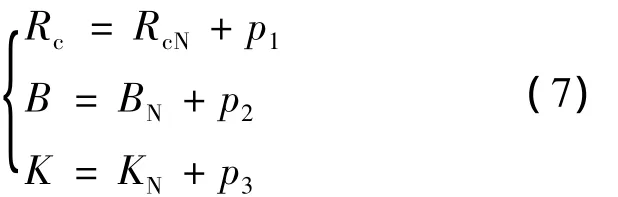
將式(5)~式(7)代入式(2)、式(3),得出具有參數(shù)攝動(dòng)陣ΔA(t)和有界擾動(dòng)w的不確定系統(tǒng):
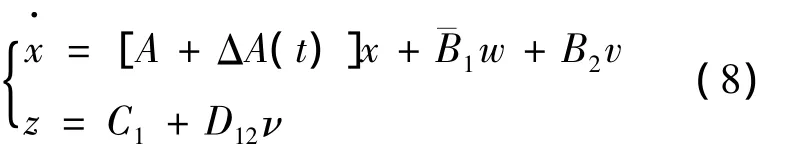
其中:x=[ΔθrΔωrΔimcΔitc]T

B1w包含非線性內(nèi)容,代入?yún)?shù)的數(shù)值后,可估計(jì)出其上界w[11]。
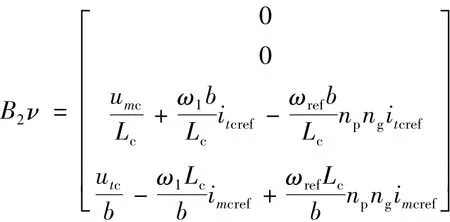
設(shè) B2ν 第 3、4 行分別等于 ν1,ν2,它們被稱為虛擬控制變量,即

4 H∞控制器的求解
式(8)符合參數(shù)不確定系統(tǒng)的H∞控制標(biāo)準(zhǔn)形式[12],第1式為被控對(duì)象,其中 ΔA(t)為參數(shù)攝動(dòng)陣,可描述為
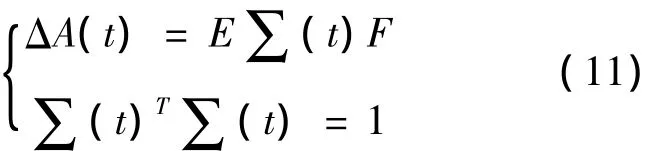
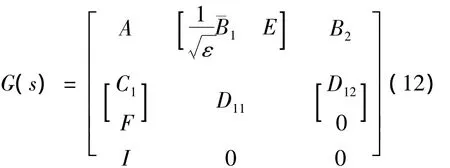
可用于求解具有魯棒穩(wěn)定、干擾抑制性能的狀態(tài)反饋控制器。式(12)中:ε>0,ε越小,意味著系統(tǒng)對(duì)干擾抑制性能越好,但過小的ε將會(huì)削弱系統(tǒng)的魯棒穩(wěn)定性;D11為零矩陣。
式(8)的狀態(tài)反饋控制器為
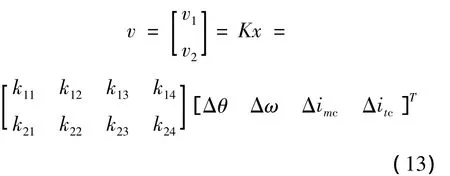
式中K為反饋系數(shù),可以用求解Riccati不等式的方法或利用MATLAB軟件中μ-分析與綜合工具箱的hinffi.m函數(shù)求取。
由式(9)、式(13)可得出無刷雙饋風(fēng)力發(fā)電系統(tǒng)的非線性H∞控制律:
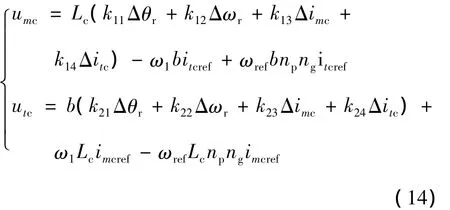
5 算例及計(jì)算機(jī)仿真
無刷雙饋型風(fēng)力發(fā)電系統(tǒng)參數(shù)如下:P1=3 kW,Up=220 V,fp=50 Hz,pp=3,pc=1,Rp=0.87 Ω,Rc=2.28 Ω,Lp=42 mH,Lc=37 mH,Lm=35 mH,風(fēng)力機(jī)槳葉半徑 R=4 m,J=500 kgm2,BN=3,KN=2,np=4,ng=7.8。在運(yùn)行過程中,不確定參數(shù)Rc,B,K變化可達(dá)其標(biāo)稱值±30%。額定風(fēng)速 υr=9 m/s,空氣密度 ρ=1.25 kg/m3。設(shè)計(jì)H∞控制器并進(jìn)行計(jì)算機(jī)數(shù)字仿真。
取 θref=0,ωref=10.3 rad/s,imcref=5 A,itcref=7 A;取可能發(fā)生的最大偏差值:p1=0.68 Ω,p2=0.9,p3=0.6。由式(2)、式(3)的說明,計(jì)算得:b=0.007 8 H,d=18.2。計(jì)算式(8)的各項(xiàng)系數(shù),按式(11)指定 E,F(xiàn),取式(12)中 ε =100。


選定加權(quán)函數(shù) C1和 D12,由式(2)、式(3)、式(16)構(gòu)成仿真模型來進(jìn)行加權(quán)函數(shù)的優(yōu)化。

求得狀態(tài)反饋控制器的反饋系數(shù)K:
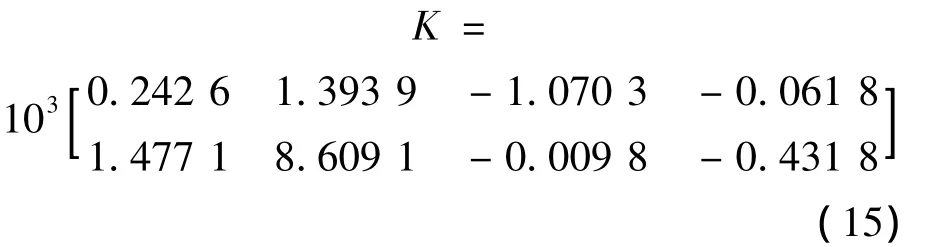
得上述無刷雙饋型風(fēng)力發(fā)電系統(tǒng)的H∞反饋控制律為
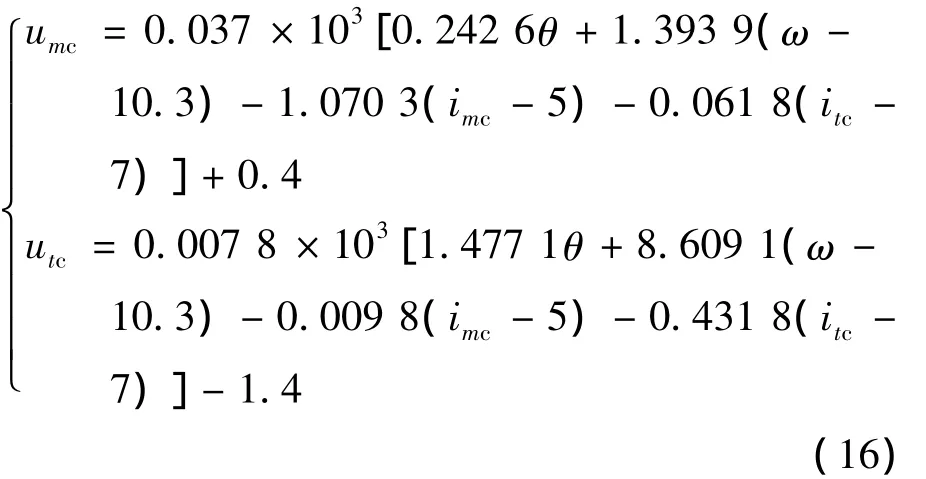
不失一般性,給出下列運(yùn)行情況作為例子進(jìn)行仿真:設(shè)不確定參數(shù)Rc=2.28±0.684 Ω,B=3+0.9sin 2t,K=2+0.6sin 3t;隨著風(fēng)速變化風(fēng)力機(jī)的轉(zhuǎn)速曲線如圖2所示,發(fā)電機(jī)輸出的有功功率指定為1.2 kW。
圖3給出了當(dāng)系統(tǒng)具有以上參數(shù)攝動(dòng)和擾動(dòng)時(shí)的仿真曲線。圖3(a)為風(fēng)力發(fā)電機(jī)輸出有功功率,圖3(b)、(c)分別為發(fā)電機(jī)控制繞組 m,t軸分量電流,實(shí)線為響應(yīng)值,虛線為期望值。圖4分別為H∞控制器的輸出電壓umc、utc。
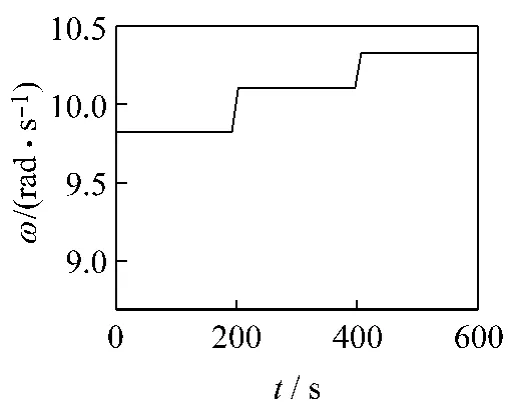
圖2 無刷雙饋型風(fēng)力發(fā)電機(jī)的轉(zhuǎn)速ω
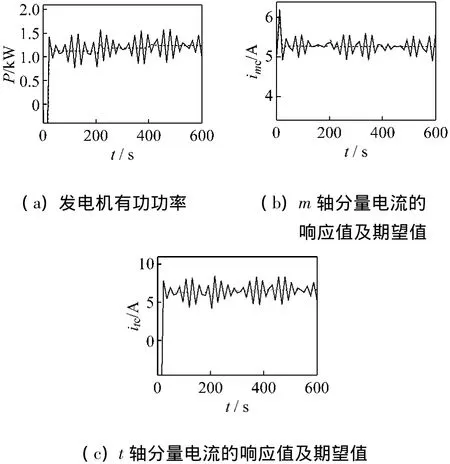
圖3 發(fā)電機(jī)有功功率、控制繞組m,t軸分量電流的響應(yīng)值及期望值
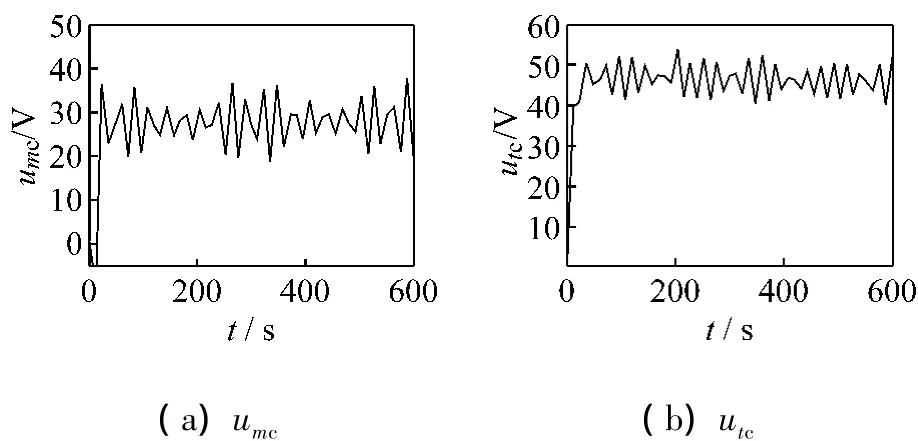
圖4 H∞控制器的輸出電壓
從仿真結(jié)果可以看出系統(tǒng)具有很好的跟蹤性能,實(shí)際響應(yīng)值跟蹤期望值,不受不確定參數(shù)和風(fēng)速變化的影響。
6 結(jié)語(yǔ)
本文對(duì)無刷雙饋型風(fēng)力發(fā)電機(jī)的H∞控制進(jìn)行了研究,建立了無刷雙饋風(fēng)力發(fā)電機(jī)的魯棒控制模型,根據(jù)H∞控制理論,利用MATLAB工具箱設(shè)計(jì)了H∞控制器。仿真結(jié)果表明,在該控制器作用下,無刷雙饋型風(fēng)力發(fā)電機(jī)具備參數(shù)攝動(dòng)鎮(zhèn)定性能和干擾抑制性能,在系統(tǒng)參數(shù)不確定的情況下,風(fēng)速變化雖然使風(fēng)力發(fā)電機(jī)的轉(zhuǎn)速隨之變化,但輸出的有功功率、控制繞組m,t軸分量電流的實(shí)際響應(yīng)值仍能很好地跟蹤期望值,安全可靠地獲取最大風(fēng)能,向電網(wǎng)輸送恒頻恒壓的電能。
[1]張先勇,舒杰,吳捷.無刷雙饋風(fēng)力發(fā)電機(jī)組的自抗擾功率解耦控制[J].太陽(yáng)能學(xué)報(bào),2008,29(12):1477-1483.
[2]黃守道,王耀南,王毅,等.無刷雙饋電機(jī)組有功和無功功率控制研究[J].中國(guó)電機(jī)工程學(xué)報(bào),2005,25(4):88-93.
[3]王琦,陳小虎,紀(jì)延超,等.基于雙同步坐標(biāo)的無刷雙饋風(fēng)力發(fā)電系統(tǒng)的最大風(fēng)能追蹤控制[J].電網(wǎng)技術(shù),2007,31(3):82-87.
[4]張先勇,吳捷,楊俊華.無刷雙饋風(fēng)力發(fā)電機(jī)滑模功率解耦控制[J].太陽(yáng)能學(xué)報(bào),2007,28(1):68-73.
[5]金鐳.基于等效旋轉(zhuǎn)控制繞組的無刷雙饋電機(jī)控制策略研究[D].沈陽(yáng):沈陽(yáng)工業(yè)大學(xué),2007.
[6]王正.轉(zhuǎn)差頻率旋轉(zhuǎn)坐標(biāo)系的無刷雙饋電機(jī)數(shù)學(xué)模型與矢量控制研究[D].沈陽(yáng):沈陽(yáng)工業(yè)大學(xué),2006.
[7]任麗娜,焦曉紅,邵立平.雙饋型變速恒頻風(fēng)力發(fā)電系統(tǒng)的魯棒控制[J].控制理論與應(yīng)用,2009,26(4):377-382.
[8]高龍.非線性系統(tǒng)的DFL及隱動(dòng)態(tài)[J].清華大學(xué)學(xué)報(bào),1996,36(9):1-9.
[9]張春朋,林飛,宋文超.基于直接反饋線性化的異步電動(dòng)機(jī)非線性控制[J].中國(guó)電機(jī)工程學(xué)報(bào),2003,23(2):99-102.
[10]蔡超豪.矢量控制異步電動(dòng)機(jī)的非線性H∞控制[J].中小型電機(jī),2004,31(1):49-52.
[11]丁剛,王勛先,韓曾晉.感應(yīng)電機(jī)的H∞抗干擾控制[J].控制理論與應(yīng)用,1999,16(4):483-486.
[12]申鐵龍.H∞控制理論及應(yīng)用[M].北京:清華大學(xué)出版社,1996:136-151.

