基于AR法的輸電塔結構三維空間風速時程模擬

汪江，陳喆，朱虹

(1.安徽省電力科學研究院，合肥市，230601;2.東南大學土木工程學院，南京市，210096)

0 引言

當前輸電塔線設計時風荷載一般按照靜力風考慮，忽略脈動風的影響［1］。實際上塔線體系中各部分動力耦合作用明顯［2］，忽略脈動風作用可能會導致計算結果存在較大誤差。但如采用現(xiàn)場實測和風洞試驗則所需周期長、花費高，因此利用計算機程序針對輸電塔結構進行脈動風速時程的精確模擬具有重要意義。

1 風速時程模擬的AR法

AR法通過線性自回歸過濾器，將人工產生的均值為零的白噪聲隨機數(shù)，輸出為具有特定頻譜特性的隨機數(shù)序列［3］。

M個點空間相關脈動風速時程V(X，Y，Z，t)的AR模型可表示為

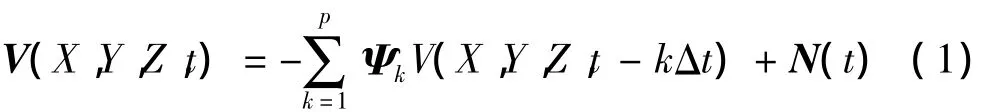
式中:Ψk為AR模型的自回歸系數(shù)矩陣;N(t)為M維獨立正態(tài)分布隨機過程向量。為簡便起見，將V(X，Y，Z，t)簡寫為 V(t)，則根據(jù)式(1)可得

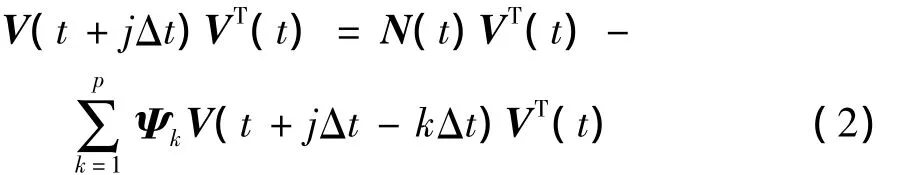
對式(2)做數(shù)學期望計算，并結合自相關函數(shù)的定義和性質，可得

式中:rV、rN分別為V(t)、N(t)的協(xié)方差矩陣。矩陣形式為

式(5)即為 AR模型的正則方程，式中，Ψ={I，Ψ1，…，Ψp}T，為(p+1)M ×M 階矩陣，I是 M 階單位矩陣;Op為pM×M階零矩陣;R為(p+1)M×(p+1)M階自相關Toeplitz矩陣

式中:rV(mΔt)是M×M階矩陣，即:

式中:m=1，…，p。

根據(jù)隨機振動理論，功率譜密度函數(shù)與相關函數(shù)滿足Wiener-Khintchine公式，即:

式中:i，j=1，…，M。當 i≠j時，Sij(n)為空間第 i，j點的互功率譜密度函數(shù);當i=j時，Sij(n)為第i點自功率譜密度函數(shù)。

通過式(7)、(8)求得式(6)后，代入式(5)，即可求解得到AR模型的系數(shù)矩陣Ψk和N(t)的協(xié)方差矩陣rN。

求得N(t)的協(xié)方差矩陣 rN后，N(t)按下式確定:

求出AR模型的系數(shù)矩陣Ψk和獨立隨機過程向量N(t)后，并假定初始時刻之前的風速為0，即t≤0時，V(t)為零向量，則由式(1)可得

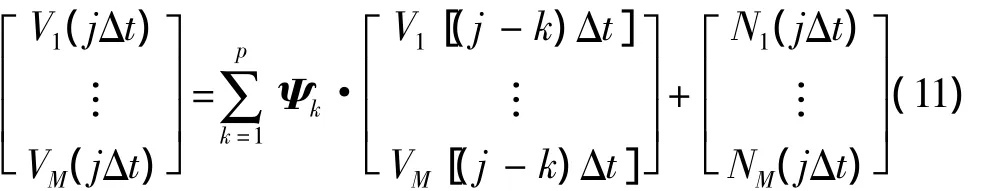
式中:jΔt=0，…，T;k=1，…，p。計算可以得到 M 個空間點的具有時間空間相關、時間步長為Δt的離散脈動風速時程向量。

2 混合編程及模擬程序實現(xiàn)

2.1 混合編程方法

Matlab語言執(zhí)行時程序逐行解釋，當包含較多循環(huán)語句時存在執(zhí)行效率低的缺點［4］。而 Visual C++擁有強大的執(zhí)行效率，可與Matlab互補以便充分發(fā)揮各自的優(yōu)勢，適合大規(guī)模數(shù)值運算。通過Matlab接口程序(application programming interface，API)，混合編程有多種實現(xiàn)方式［5］。

本文采用Visual C++編寫具有一定格式的程序(*.c函數(shù)的形式)，經(jīng)過編譯生成的Matlab動態(tài)鏈接子程序(*.dll函數(shù)的形式)，即MEX文件，然后以子函數(shù)或子過程的形式提供給Matlab應用程序，可以實現(xiàn)直接調用［6］。

2.2 程序實現(xiàn)

Matlab強大的矩陣運算功能及豐富的庫函數(shù)，可簡化風速模擬程序的編制，節(jié)省代碼并減小出錯，提高程序開發(fā)效率。如偽隨機數(shù)的生成，通過調用rand函數(shù)，理論上其樣本空間為21492個［7］。其他如矩陣相乘、除，矩陣的Cholesky分解，快速傅里葉變換(fast fourier transform，F(xiàn)FT)運算，風速時程的功率譜估計及繪圖等均可以通過Matlab相應的運算格式和調用相應的庫函數(shù)來實現(xiàn)，庫函數(shù)可根據(jù)問題自動采用最優(yōu)算法，保證了計算精度和模擬求解的穩(wěn)定性。

在編制采用AR法模擬風速的程序時，為了保證數(shù)值積分運算求解精度，須經(jīng)過大量循環(huán)迭代運算。Romberg定積分算法可提高計算效率和求解精度。為測試編制好的 Visual C++語言 Mex源文件rombergwk.c的迭代計算是否正確，下面采用該程序計算積分

＞＞ rombergwk(1，1，1，2，10－4) ［注:前2 個入口參數(shù)對此積分不需要，故任意取為1。其中截斷誤差(計算精度)為 10－4］

與ln2=0.693147相比，該結果的精度較高，而且還可以通過最后1個入口參數(shù)(10－4)來控制精度，證明了該程序迭代計算的正確性。通過結合各類風速譜函數(shù)編制程序時應寫成Mex文件，在Matlab中編譯連接后方可實現(xiàn)其對Visual C++語言程序的直接調用。

風速模擬程序運行環(huán)境為Windows XP SP3系統(tǒng)，AMD Turion(tm)64 X2 TL －581.90 GHz處理器，1.00 GB內存，Matlab 版本為7.0。采用混編技術計算用時1267.5 s，未采用混編技術計算用時2520.7 s，幾乎是采用混編技術用時的2倍。由此可看出混合編程后，運算速度與執(zhí)行效率大為增加。

3 算例分析

自立式輸電塔屬于空間桿件體系，可采用空間桿單元和梁單元建立輸電塔的有限元模型［8］。鑒于輸電塔自重較輕，自重二階效應不明顯，數(shù)值分析時可將輸電塔視為線性結構進行計算［9］。圖1為2E2-SZ2型220 kV輸電塔三維模型。

圖1 2E2-SZ2型220 kV輸電塔三維模型Fig.1 220 kV 2E2-SZ2 transmission tower model

塔架總高 58.7 m，節(jié)點總數(shù) 624，單元總數(shù)1602，其中迎風面節(jié)點總數(shù)為161，迎風面單元總數(shù)為325。

利用自編AR脈動風模擬程序，得到了考慮空間相關的多點水平脈動風模擬結果，模擬過程中，主要參數(shù)由表1給出。

表1 風模擬程序主要參數(shù)Tab.1 Main parameters of simulation program

采用Welch法［10］得到功率譜。部分節(jié)點的水平風速模擬時程曲線及功率譜如圖2所示。

對輸電塔結構節(jié)點沿高度繪制功率譜后發(fā)現(xiàn)，高度位于35 m以下的節(jié)點，低頻部分與高頻部分模擬譜與目標譜之間逼近較好，個別節(jié)點中部分模擬譜與目標譜誤差略大;高度位于35 m以上部分高低頻部分模擬譜均與目標譜有一定誤差，且隨著高度增加有擴大的趨勢。事實上，若采用Bartlett［11］法繪制功率譜，低頻部分為平直型折線，高頻部分為近似以目標譜為分界，呈上下震蕩型折線，低頻部分誤差更為明顯。因此綜合考慮為減小瞬態(tài)效應，計算時可考慮忽略前面部分時程點數(shù)據(jù)。程序運行期間快速穩(wěn)定，說明Visual C++與Matlab混合編程切實有效，圖2中各點模擬功率譜與目標譜總體吻合良好，證明所編制風速時程程序的正確性。需要注意的是，模擬時間步長不宜小于0.1 s，時間步長過小時模擬精度大為降低，易產生錯誤。

圖2 節(jié)點水平風速模擬時程曲線及功率譜Fig.2 The simulation time-history curves of horizontal wind speeds and power spectrum

4 結語

(1)三維空間風速時程的精確模擬是進行輸電塔結構非線性風振響應分析的基礎。本文針對輸電塔的三維空間分析模型，采用混合編程機制編制的風速時程模擬程序具有良好的計算效率和穩(wěn)定性。

(2)不同高度處節(jié)點的脈動風速時程趨勢基本接近，但隨著高度的增加，脈動風速波動范圍略有減小，表明輸電塔結構體系的脈動特性隨著高度的增加略有降低。

(3)由于Davenport譜紊流尺度沿高不變，對于一般構筑物，如常見輸電塔、預應力網(wǎng)殼結構、橋梁等結構均可用本風速時程模擬程序模擬風速，因而本程序有一定的通用性。

［1］DL/T 5092—1999P 110～500 kV架空送電線路設計技術規(guī)程［S］.北京:中國電力出版社，1999.

［2］ MomomuraY，MarukawaH，OkamuraT，etal. Full-scale measurements of wind-induced vibration of a transmission line system in a mountainous area［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，72(1):241-252.

［3］周云.結構風振控制的設計方法與應用［M］.北京:科學出版社，2009.

［4］劉保柱，蘇彥華，張宏林.Matlab7.0從入門到精通［M］.北京:人民郵電出版社，2010.

［5］王素立.Matlab混合編程與工程應用［M］.北京:清華大學出版社，2008.

［6］董振海.Matlab編譯程序和外部接口［M］.北京:國防工業(yè)出版社，2010.

［7］舒新琳，周岱.風速時程AR模型及其快速實現(xiàn)［J］.空間結構，2003，9(4):27-32.

［8］徐建國，石華軍，郭勇，等.大跨越輸電塔線體系有限元建模［J］.電力建設，2011，32(3):15-19.

［9］王肇民，Peil U.塔桅結構［M］.上海:同濟大學出版社，1989:196-253.

［10］李志敏.預應力網(wǎng)殼結構的風振響應研究［D］.南京:東南大學，2007.

［11］鄒鯤，袁俊泉，龔享銥.Matlab6.x信號處理［M］.北京:清華大學出版社，2002.