穩定控制回路振鈴現象的消除及其關鍵參數的選擇＊

王文亮

（海軍駐南昌地區某軍事代表室 南昌 330024）

1 引言

在用Dahlin提出的閉環響應方法設計數字控制器時，不僅應關心系統的閉環響應，同時還應注意控制器輸出量的上下變化。因為Dahlin控制器經常會產生所謂的振鈴問題，它會使調舵面頻繁地上下偏轉，加速控制設備的磨損。這一現象在提出Dahlin控制器時就已被發現，并給出了修正設計方法［1～2］。后來又對此進行了分析。從修改期望的閉環傳遞函數入手提出一種新的設計方法。借助于內模結構分析了Dahlin控制器產生振鈴的本質原因，指出Dahlin修正設計方法不能完全消除純滯后引起的振鈴，并針對一階對象發展了一種能夠避免振鈴的更好的設計方法［3］。

本文將在以前研究的基礎上，討論Dahlin控制器存在振鈴的可能性。首先，在復頻域分析的基礎上探討了二階對象期望閉環傳遞函數的合理形式。然后，通過對期望閉環傳遞函數和控制對象的分析找到了導致二階對象Dahlin控制器產生振鈴的原因，給出了判定振鈴產生的條件。并且提出了修正設計方法。最后，以空地導彈穩定控制回路為例，通過對所建回路的分析并結合解決振鈴現象中關鍵參數的選擇方法，得出了單位階躍信號下，穩定控制回路數字控制器的控制信號序列u（k）得到明顯改善。本研究對于今后導彈控制效率的設計和提高控制系統的控制效率有著重要的研究和指導意義。

2 振鈴現象及其消除方法

所謂振鈴（ringing）現象，是指數字控制器的輸出以1／2采樣頻率大幅度衰減的振蕩。本文以俯仰通道為例，控制回路的結構圖如圖1所示，數字控制器輸出控制信號序列u（k）如圖2所示。由于被控對象中慣性環節的低通特性，使得這種振蕩對系統的輸出幾乎無任何影響［4］。但是振蕩現象卻會增加執行機構的磨損，在有交互作用的多參數控制系統中，振鈴現象還有可能影響到系統的穩定性［5］。

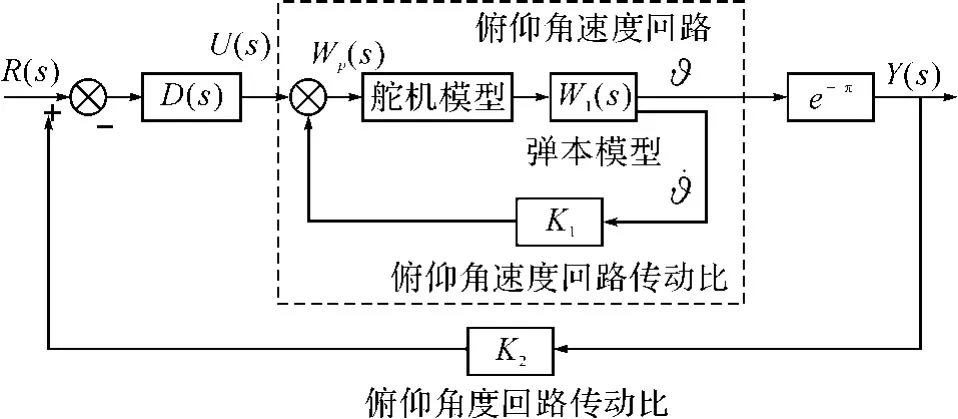
圖1 導彈穩定控制回路結構圖

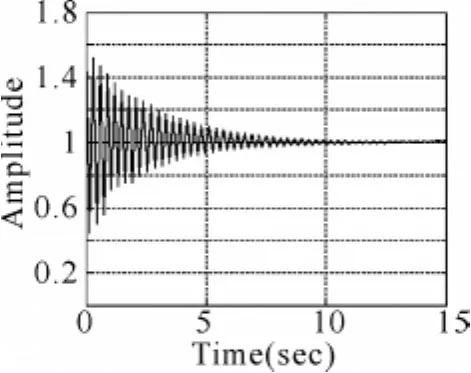
圖2 系統的控制信號序列

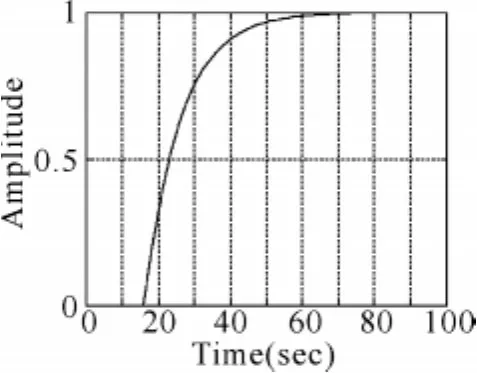
圖3 系統的階躍響應序列

設被控對象為帶有純滯后的二階環節，即

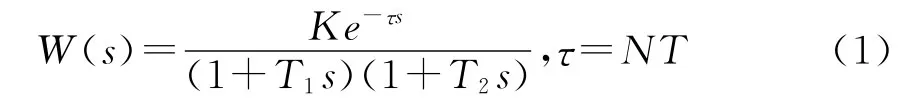
對象為具有純滯后的二階慣性環節時，其z傳遞函數為

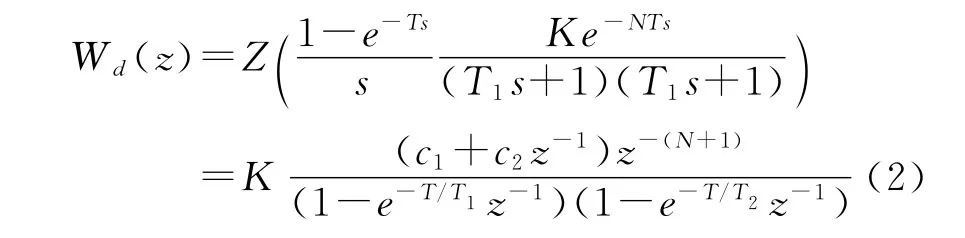
控制器的傳遞函數為式中

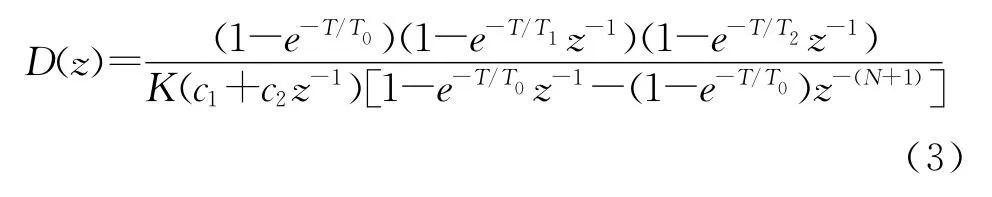
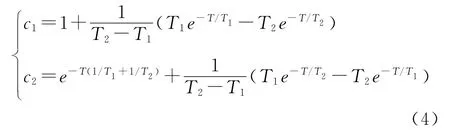
振鈴現象與被控對象的特性、閉環時間常數、采樣周期、純滯后時間的大小等有關，下面對振鈴現象產生的原因進行分析。控制器輸出U（z）與參考輸入R（z）之間的關系為

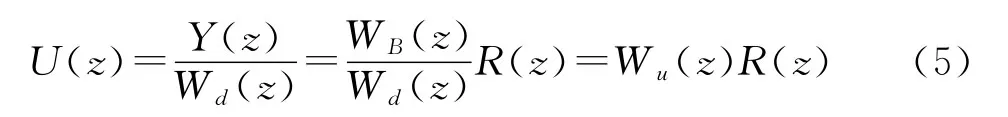
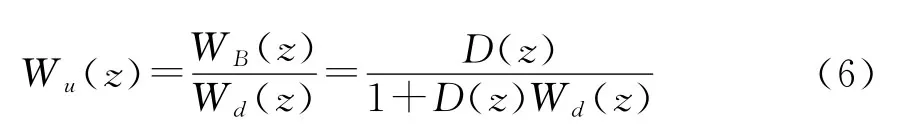
是U（z）到R（z）的閉環脈沖傳遞函數。

對于單位階躍輸入函數R（z）＝1／（1－z－1），含有z＝1的極點，如果Wu（z）的極點在z平面的負實軸上，并且與z＝－1點相近，則由暫態過程可知，數字控制器的輸出序列u（k）中將含有這兩種幅值相近的瞬態項，而且瞬態項的符號在不同時刻是不相同的。當兩瞬態項符號相同時，數字控制器的輸出控制作用加強，符號相反時，控制作用減弱，從而造成數字控制器輸出序列大幅度波動，這就是造成振鈴現象的主要原因［6～7］。

對于帶純滯后的二階慣性環節，有

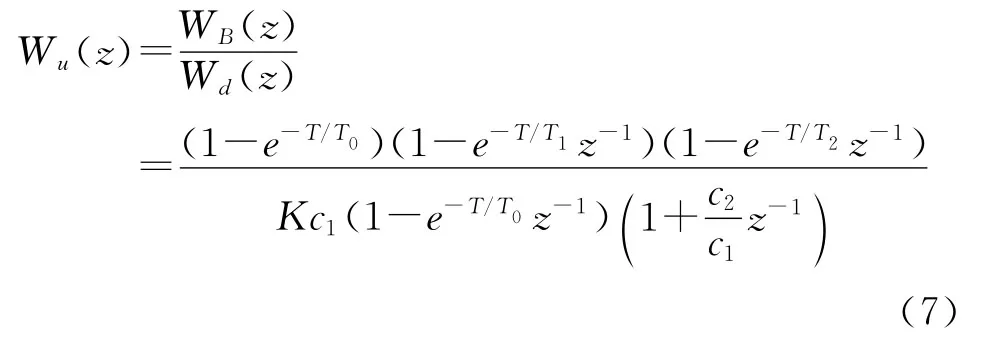
式中

式（7）中有兩個極點，第一個極點在z＝e－T／T0，不會引起振鈴現象；第二個極點在z＝－c2／c1。由式（5）知，在T→0時，有

這說明可能出現負實軸上與z＝－1相近的極點，這一極點將引起振鈴現象。

振鈴現象的強度用振鈴幅度RA來衡量，通常采用在單位階躍作用下數字控制器第0拍輸出與第1拍輸出的差值來衡量振鈴現象強烈的程度［8］。

由式（3）可知，Wu（z）是z的有理分式，寫成一般形式為

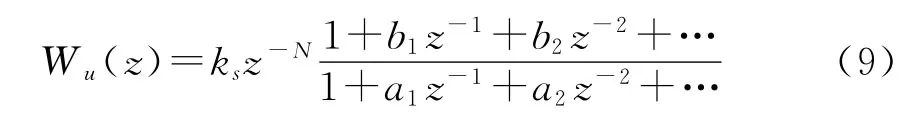
忽略比例系數ksz－N的影響（相當于進行了歸一化處理），在單位階躍輸入函數的作用下，數字控制器輸出量的z變換為

所以

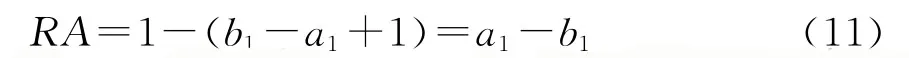
對于純滯后的二階慣性環節組成的系統，其振鈴幅度由式（4）可得

消除振鈴現象的方法是：先找到D（z）中引起振鈴現象的因子（z＝－1附近的極點），然后令其中的z＝1。根據終值定理，這樣不影響輸出的穩態值，但往往可以有效地消除振鈴現象。這一點可以通過式（3）得到驗證，因為控制器D（z）的極點就是閉環脈沖傳遞函數Wu（z）的極點，因此Wu（z）中z＝－1附近的極點實際上包含在控制器D（z）的分母中［9］。

對于帶純滯后的二階慣性環節系統中，數字控制器D（z）如式（3）所示，其極點z＝－c2／c1將引起振鈴現象。令極點因子c1＋c2z－1中z＝1，就可以消除這個振鈴極點。由式（4）得

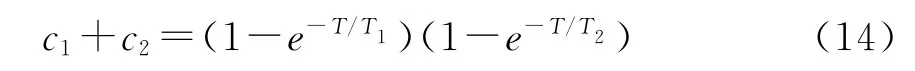
消除振鈴極點后控制器的形式為

根據式（8），當T→0時，有

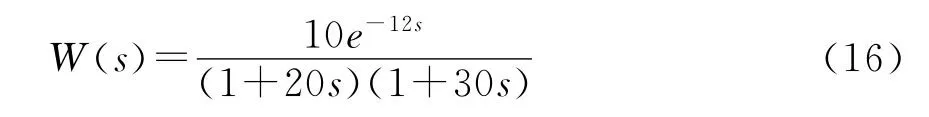
取采樣周期T＝2s，可知T1＝20，T2＝30，K＝10，N＝τ／T＝6，所設計的數字控制器傳遞函數模型為

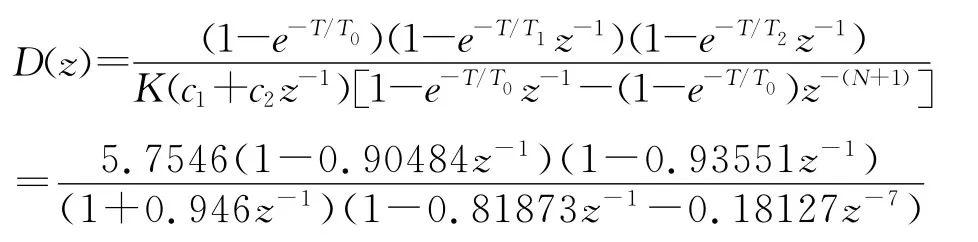
這種消除振鈴現象的方法雖然不影響輸出穩態值，但卻改變了數字控制器的動態特性，將影響閉環系統的暫態性能。

計算俯仰通道穩定控制回路的被控對象模型為純滯后的二階慣性環節

其中極點z＝－0.946將引起振鈴現象，因此令（1＋0.946z－1）的因子中z＝1，于是控制器傳遞函數模型變為

以此控制器組成計算機控制系統進行控制，階躍函數輸入下系統的響應如圖4所示。與圖1相比，可以看出控制信號序列u（k）得到了很好的抑制，消除了振鈴現象，但是系統輸出響應的動態過程發生了變化，出現了超調，且過渡過程時間變長。

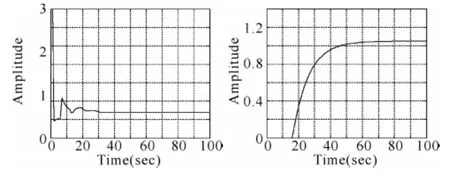
圖4 令振鈴因子z＝1后系統的控制信號和輸出信號曲線

3 解決振鈴現象中關鍵參數的選擇

關于振鈴現象的解決，前面已經介紹了通過令控制器傳遞函數中振鈴因子式中的z＝1的方法加以消除，但結果是改變了控制器模型的結構，因此常常造成控制系統的動態性能變差，出現了如超調、過渡過程時間變長等。

有些工業應用場合，在盡量消弱振鈴幅度的同時，不希望系統的動態性能有太大的改變，這種情況下可以通過選擇合適的采樣周期T及閉環系統時間常數T0＝1得以實現。

從式（12）可以看出，帶純滯后的二階慣性環節組成的系統中，振鈴幅度與被控對象的參數T1、T2有關，與閉環系統期望時間常數T0以及采樣周期T也有關。前者是被控對象固有的參數，無法改變，因此可以通過適當選擇T和T0，把振鈴幅度抑制在最低限度以內。在此情況下，閉環系統時間常數T0作為控制系統的性能指標被首先確定了，但還可以通過式（12）選擇采樣周期T來抑制振鈴現象。

對于純滯后系統，通過選擇關鍵參數T和T0，削弱振鈴現象影響的大林算法數字控制器設計的一般步驟如下［10］：

1）根據系統的性能，確定閉環系統的參數T0，給出振鈴幅度RA的指標。

2）由式（12）所確定的振鈴幅度RA與采樣周期T的關系，解決給定振鈴幅度下對應的采樣周期T，如果T有多解，則選擇較大的采樣周期。

3）確定純滯后時間τ與采樣周期T之比（τ／T）的最大整數倍N。

4）計算對象的脈沖傳遞函數Wd（z）及閉環系統的脈沖傳遞函數WB（z）。

5）計算數字控制器的脈沖傳遞函數D（z）。

由俯仰通道穩定控制回路的被控對象模型可知，T1＝20，T2＝30，K＝10，取T0＝10。

選擇采樣周期T。根據式（12）振鈴幅度與采樣周期的關系如下：

由上面的數據可以看出，采樣周期加大，振鈴幅度并沒有明顯地減小，因此，選取采樣周期T＝4s。

確定純滯后時間τ與采樣周期T之比，N＝τ／T＝12／4＝3。

確定對象的脈沖傳遞函數。根據式（2）和式（4），有

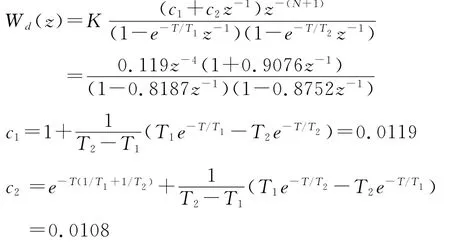
根據式（3），得數字控制器的傳遞函數模型為

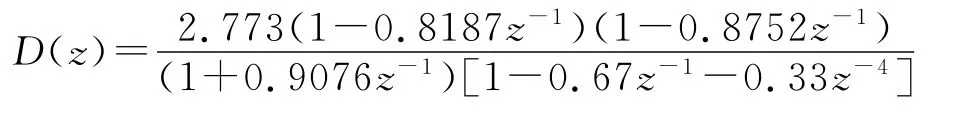
此控制器組成計算機控制系統進行控制，階躍函數輸入下系統的響應如圖5所示。從圖中可以看出，控制信號序列u（k）的振蕩幅度同圖2相比，明顯減弱，但是輸出信號動態過程變化不大。

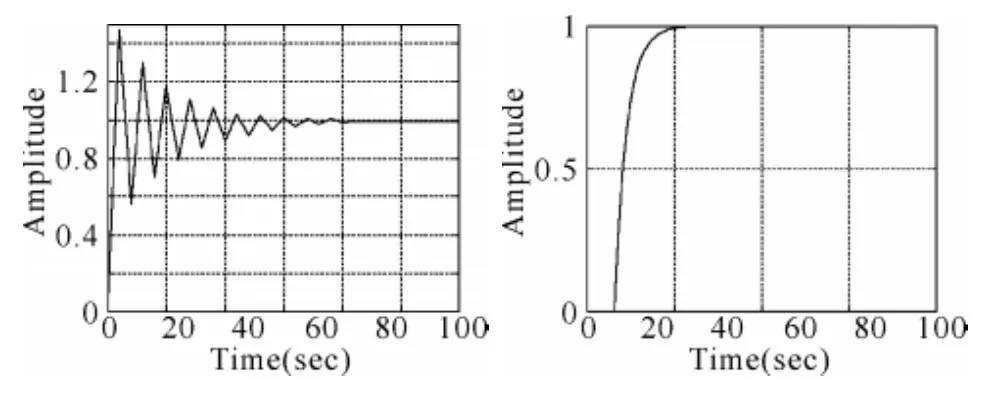
圖5 調整采樣周期后的系統控制信號和輸出信號曲線

4 結語

Dahlin控制器是一種常見的數字控制器，由于振鈴問題的存在限制了它的應用。以往的對振鈴問題研究是根據經驗進行的，本文則在通過以導彈穩定控制回路為對象，分析探討了二階對象Dahlin控制器的設計問題，通過系統輸入到控制輸出的傳遞函數證明，振鈴的產生與期望閉環傳遞函數無關，而在于控制對象離散化時可能產生的負零點。令D（z）中引起振鈴現象的因子（z＝－1附近的極點）z＝1，此方法能消除振鈴現象，但會改變控制器模型的結構，因此常常造成控制系統的動態性能變差。為此，選擇采樣周期T來抑制振鈴現象。仿真研究表明，此方法能夠有效消除振鈴。這對于今后導彈穩定控制回路的設計和有效提高控制系統的控制效率有著重要的研究和指導意義。此方法不但適用于導彈回路，對于過程控制中存在振鈴現象的控制回路，均能有效抑制振鈴現象，具有很廣闊的應用前景。

［1］奧斯特羅姆K J，威特馬克B.計算機控制系統［M］.王曉陵，等譯.哈爾濱：哈爾濱船舶工程學院出版社，1987：36～37

［2］曹立學.大林算法在MIMO大滯后控制系統中的設計研究［J］.計算機與數字工程，2008，36（7）：4～6

［3］俞挺，陳應麟.達林算法在管道溫度控制中的應用［J］.電氣自動化，1998，20（4）：11～12

［4］李國勇，謝光明.控制系統數字仿真與CAD［M］.北京：電子工業出版社，2003：50～51

［5］郭東道.多變量系統設計的頻率域方法［M］.西安：西北大學出版社，2004：13～15

［6］范承亞，謝宋和.Dahlin算法絕對穩定分析［J］.石油大學學報（自然科學版），1990，14（5）：95～100

［7］劉建昌，關守平，周瑋，等.計算機控制系統［M］.北京：科學出版社，2009：55～57

［8］王錦標.計算機控制系統［M］.北京：清華大學出版社，2008：46～48

［9］柴天佑.多變量自適應解耦控制及應用［M］.北京：科學出版社，2001：22～24

［10］孫增圻.計算機控制理論與應用［M］.北京：清華大學出版社，2008：38～40