基于模糊層次分析法的產品特性分類模型

李鵬舉，程中華，李欣玥

（軍械工程學院 裝備指揮與管理系，石家莊 050003）

0 引言

產品特性分類工作由設計部門負責，是指在特性分析（技術指標分析、設計分析和選定檢驗單元）的基礎上確定配套產品的關鍵件、重要件和一般件[1]。其目的是將設計人員對重點產品控制意圖傳遞給工藝、制造、采購和檢驗部門，以便在各環節中采取重點預防、監督、管理的措施，保證產品質量的穩定性和可追溯性。產品特性分類是武器裝備研制設計的重要環節，也是各級有關部門、合同商實行重點控制的主要依據[2]。

根據產品可能出現故障后果的嚴酷度等級及故障發生概率，當前產品特性分類方法主要有風險優先數（RPN，Risk Priority Number）法和危害性矩陣法。這兩種方法著重考慮的是產品的安全性，而忽略了裝備壽命期中的維修性、保障性因素。文章針對這些不足，在原有特性分類方法的基礎上，采用系統工程中的層次分析法將定性指標和定量指標相結合考慮，滿足了特性分類指標多樣化的要求。同時，根據準則權重和評分結果得出的產品優劣排序，可以輔助指導設計人員按照關鍵件、重要件比例進行產品特性分類工作。

1 模糊層次分析法基本過程

層次分析法（AHP，Analytical Hierarchy Process）是美國運籌學教授Saaty于20世紀70年代提出了一種定性分析和定量分析相結合的系統分析法。它通過建立層次結構模型和判斷矩陣的方式對層次中的元素進行排序，從而把一個復雜的決策問題簡單化，為解決問題提供客觀依據。為了改進AHP中諸如判斷一致性與矩陣一致性的差異、一致性檢驗困難和缺乏科學性等問題，一些學者提出模糊層次分析法（FAHP，Fuzzy AHP）。與AHP相比，FAHP通過元素兩兩比較構造模糊一致性判斷矩陣，更符合人的思維和心理特點，并解決了AHP存在的一些問題，因此FAHP在決策分析中得到了廣泛的應用。

1.1 建立層次結構

應用層次分析法進行產品特性分析決策時，首先要建立評價問題的層次結構。層次結構是應用層次分析法把復雜問題分解簡化的關鍵，必須在對評價原則和意圖深刻分析理解的基礎上進行。結構中的最上層是評估目標，中間層是準則層，最底層是評價對象（產品層）。準則層可以包含多級，同級之間相互獨立，上下級之間為隸屬關系[3]。

參照GJB 190—86《特性分類》相關規定，結合產品特性分類工作實際，建立產品特性分類層次結構圖，如圖1所示。

在進行產品特性分類過程中，首先采用關鍵件特性準則對系統或單機內的所有產品進行評價排序；由分析人員按照關鍵件比例要求確定關鍵件后，再應用重要件特性分類準則對剩余器件進行評價排序；最后按照比例要求確定重要件和一般件。

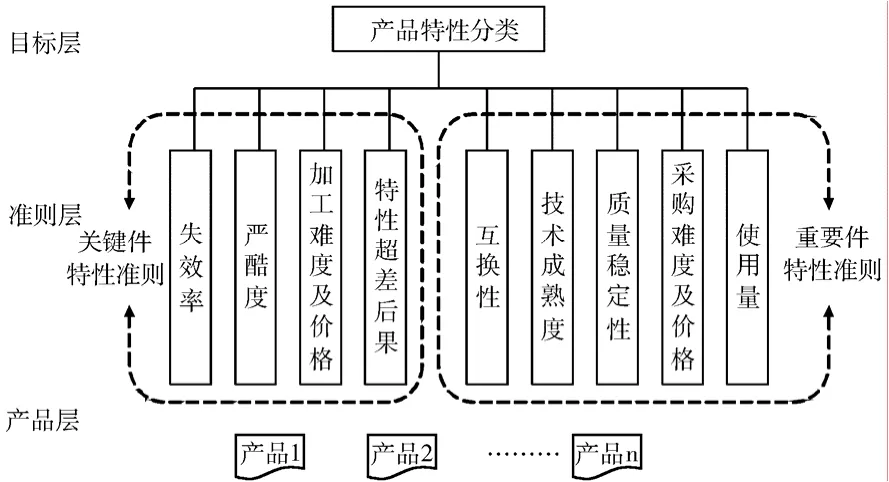
圖1 產品特性分類層次結構Fig.1 Hierarchy of the classification of product characteristics

1.2 構造模糊判斷矩陣

模糊判斷矩陣R表示在層次結構中，針對隸屬的上一級元素，某一級元素之間相對重要性的比較矩陣。例如：假定上一級元素為B1，它與下一級中的元素C1、C2、…、Cn、有隸屬聯系，經過專家的模糊判斷，可得矩陣為

其中rij表示元素Ci相對元素Cj的重要程度的度量值，通常采用1～9標度法，如表1所示。

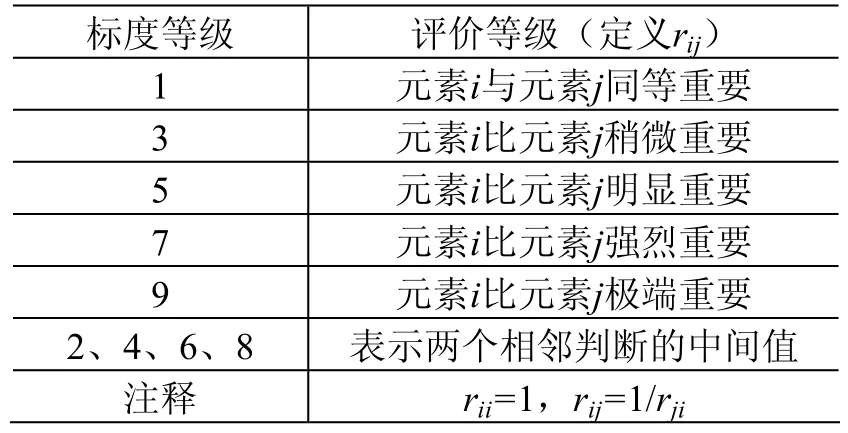
表 1 1～9標度法及其意義Table 1 Meaning of the 1～9 scaling levels

利用模糊判斷矩陣計算各特性所占權重方法很多，本文選用以下公式[5]：

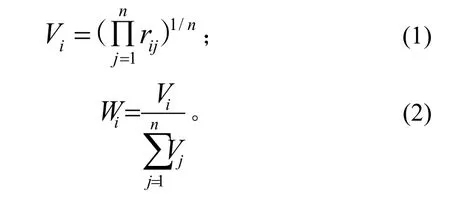
其中：V為中間變量；ij12,n=…、,,。 得出的權重向量表達式為

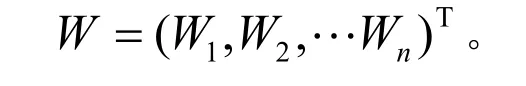
1.3 模糊判斷矩陣的一致性檢驗

由模糊判斷矩陣得到的權重值是否合理，需要進行一致性檢驗。模糊判斷矩陣的一致性反映判斷者思維的邏輯一致程度。當偏離一致性過大時，將此權重向量的計算結果作為決策依據是不可靠的[4]。

檢驗模糊判斷矩陣一致性的公式為

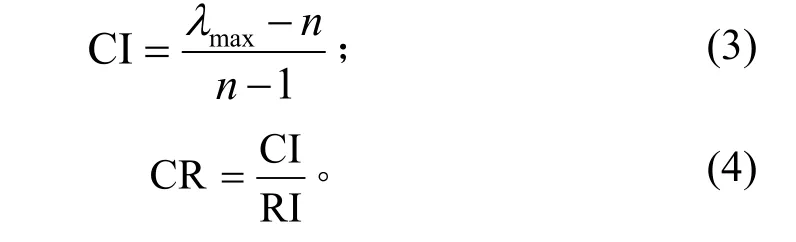
其中：CR為判斷矩陣的一致性比率；maxλ為模糊判斷矩陣的最大特征值；n為矩陣階數（1＞n）；RI為平均隨機一致性指標，如表2所示。

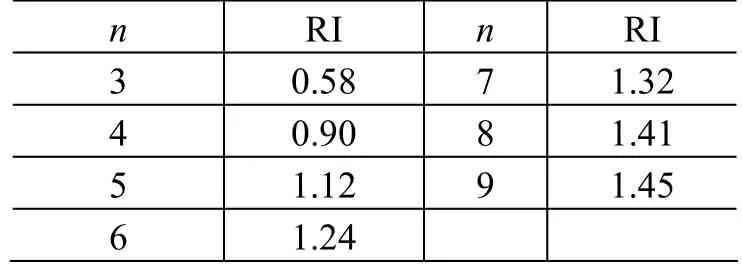
表 2 平均隨機一致性指標Table 2 Mean random consistency index(RI) of 3-order through 9-order

如果 C R = CIRI＜0.1，則此模糊判斷矩陣具有滿意的一致性，評價結果是可靠的，否則就需要進行調整。一般對于三階以上的判斷矩陣才需要檢驗一致性。

1.4 確定專家權重

在對特性分類準則進行模糊評判的過程中，不同專家由于受到知識結構、評判水平和自身偏好等因素的影響，所作出的模糊判斷矩陣的質量和側重方面必然存在差異。因此，在最終確定各特性分類準則所占權重時，不能簡單地將每位專家的結果相加求平均值，應有區別地對待。目前，確定專家的權重有兩種方法：第一種方法是通過專家所做的模糊矩陣一致性程度來確定；另一種方法則通過不同專家所做的模糊矩陣相似程度來確定。本文選用第二種方法[5]。

設有m(m＞ 1)位專家參與人為差錯影響因素的評判，第k位專家的模糊互補判斷矩陣為

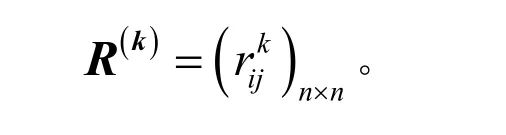
計算得第k位專家所確定的特性分類準則權重向量為

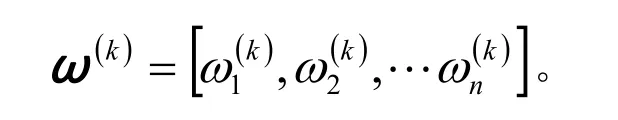
設θ表示權重向量ω(k)與ω(l)的夾角，θ的余弦

klkl定義為

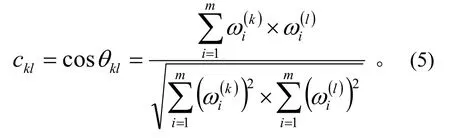
c表示權重向量ω(k)與ω(l)的相似程度，即專家

kl k與專家l判斷的一致程度，c越大，表明ω(k)與

kl ω(l)越相似。

計算每個權重向量與其他權重向量的夾角余弦后，可得到矩陣

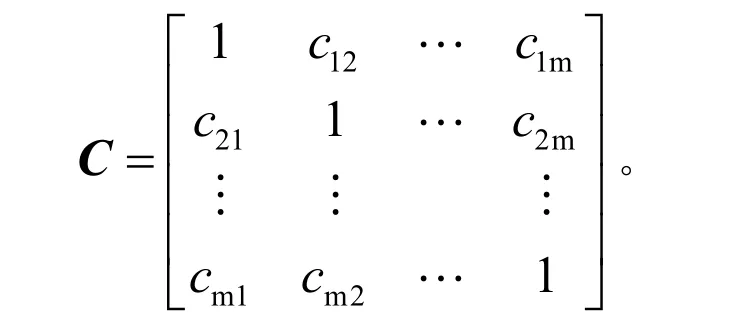
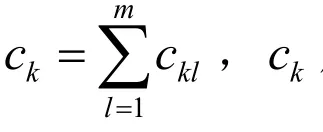
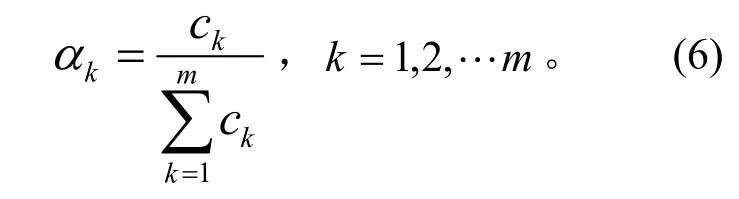
最后得出綜合專家權重的特性準則權重向量為

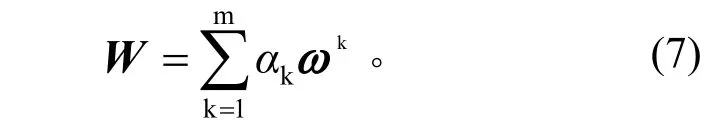
2 案例計算

現對某新型號雷達的發射機調制器組合進行產品特性分類。調制器組合是雷達發射機中的重要組成部分，其主要作用是給雷達發射機的行波管提供正負偏壓、燈絲電壓以及調制脈沖。

首先邀請3位不同領域的專家對關鍵件和重要件的特性分類準則作兩兩比較判斷，得出互補模糊判斷矩陣。第一位專家的模糊判斷數據如表3所示。

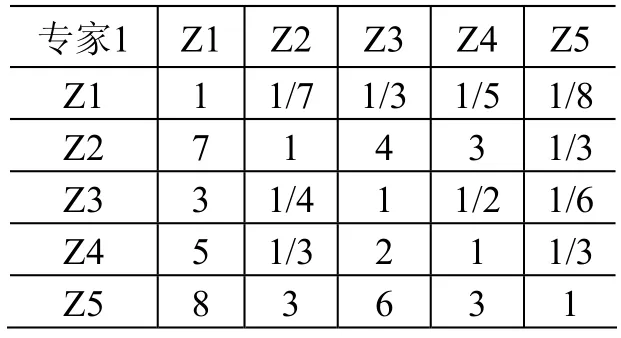
表3 專家1模糊判斷數據Table 3 Fuzzy judgment data of expert A

專家1的模糊判斷矩陣為

根據式(1)、(2)計算出專家1的特性準則權重向量為

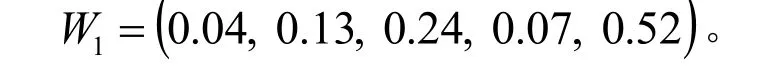
類似可得專家2和專家3的權重向量分別為

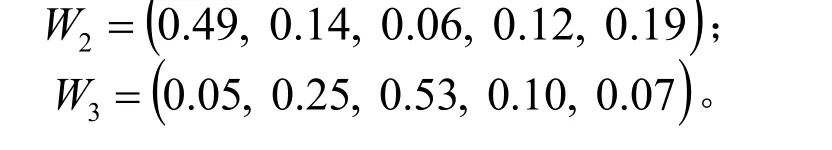
根據式(3)、(4)計算得出3位專家的模糊判斷矩陣一致性指標分別為CR1=0.043 3、CR2=0.001 1、CR3=0.001 3，滿足一致性指標要求。

由式(5)得到的專家權重計算矩陣C為

由式(6)得到3位專家權重分別為0.35、0.32、0.33，最終可算得重要件特性分類準則的權重為

關鍵件特性分類準則的權重為

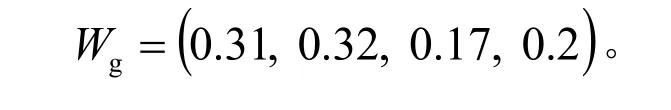
3 軟件開發

筆者運用Borland Delphi 7.0和Microsoft Access 2007軟件工具開發了基于模型的產品特性分類軟件，界面如圖2、圖3所示。將專家模糊判斷矩陣和器件目錄導入到特性分類軟件中后，分析人員對器件的各種特性按照1～10標度進行逐一打分，根據隸屬度原則，加權計算后得出優劣排序，最終可以按照關鍵件、重要件的比例要求完成產品特性分類工作。

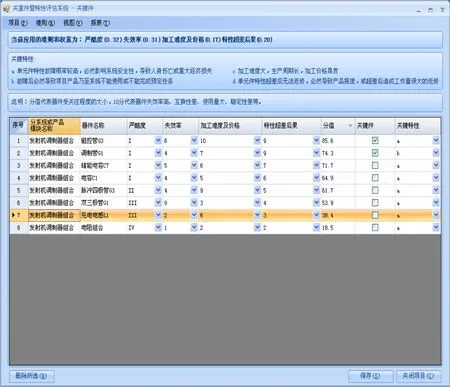
圖2 關鍵件評價Fig.2 Assessment of key products

圖3 重要件評價Fig.3 Assessment of important products

4 結束語

在原有的產品特性分類方法基礎上建立的評價指標體系，綜合考慮了安全性、維修性、保障性因素，提高了特性分類結果的客觀性和可信度。FAHP能夠科學確定相關特性分類準則權重，既避免了權重確定中的隨意性，又考慮了主觀思維判斷的模糊性，是一種思路清晰、可操作性強的權重計算方法。案例分析結果表明：基于FAHP的產品特性分類方法及軟件能夠有效提高產品特性分類工作的科學性和效率，是對現有方法的補充和完善。

（References）

[1]陳圣斌, 周曉光.直升機可靠性關鍵件和重要件的確定方法及工程應用[C]//中國航空學會直升機專業分會第十九屆全國直升機年會.哈爾濱： 中國航空學會,2004： 314-320

[2]李鳳良.航天型號產品特性分類工作基本狀況與建議[J].航天標準化, 2001(5)： 17-18

Li Fengliang.The base situation and some suggestions about classification of product’s characteristics of space product[J].Aerospace Standardization, 2001(5)： 17-18

[3]段秉乾, 司春林.基于模糊層次分析法的產品創新風險評估模型[J].同濟大學學報： 自然科學版, 2008,36(7)： 1002-1005

Duan Bingqian, Si Chunlin.Comprehensive risk assessment model of complex product systems innovation based on fuzzy AHP[J].Journal of Tongji University： Natural Science, 2008, 36(7)： 1002-1005

[4]王雪青, 劉姍姍, 郭曉博.基于模糊層次分析法的代建制企業風險評價[J].北京理工大學學報： 社會科學版, 2008, 10(3)： 73-76

Wang Xueqing, Liu Shanshan, Guo Xiaobo.A risk evaluation of the agent construction company based on FAHP[J].Journal of Beijing Institute of Technology：Social Science Edition, 2008, 10(3)： 73-76

[5]劉風強, 孫志強, 謝紅衛.航空維修人為差錯影響因素分析中的模糊層次分析法[J].中國安全科學學報,2008,18(7)： 43-48

Liu Fengqiang, Sun Zhiqiang, Xie Hongwei.Analysis of human error influence factors in aviation maintenance based in group fuzzy analytical hierarchy process[J].China Safety Science Journal, 2008, 18(7)： 43-48