變點交叉多目標遺傳算法在作業車間調度中的應用
劉婷
(大連交通大學 軟件學院,遼寧 大連 116028)
0 引言
大多數車間調度問題屬于多目標問題,一般來說,它各個優化目標之間通常相互沖突,即不可能同時在所有目標上都達到最優,只能在多個目標之間進行協調和權衡[1].求解多目標調度的傳統方法是將其轉化為單目標優化問題進行處理,如多目標加權法、層次優化法等.多目標遺傳算法具有處理大的問題空間的能力,在一次進化過程中可以得到多個可行解曲面,對問題域的先驗知識沒有要求,對函數定義域的凸性不敏感,這正是經典算法所不具備的[2].所以,應用遺傳算法求解車間調度多目標優化問題,是這一領域的發展趨勢.本文采用多點交叉的方式,提高收斂速度,預防早熟,同時采用交互權重方式使決策人的偏好盡可能得到滿足,將多目標問題轉化為單目標問題.
1 新的交互式多目標遺傳算法的基本思想
本文采用變點交叉的方式來提高多目標遺傳算法的收斂速度,避免其局部收斂,引起早熟.同時針對傳統的多目標遺傳算法忽略決策者偏好這一問題設計一種交互權重,改進之處有以下兩點:①采用變點交叉的方式彌補多目標遺傳算法在解決作業車間調度問題時收斂速度慢和容易陷入局部最優化的不足;②利用代理值置換法(SWT)[3]的思想對各目標兩兩權衡分析,設計一種交互權重,從而簡化多目標問題,體現決策者偏好.
1.1 變點交叉的方式
對于多目標遺傳算法在解決車間調度問題中存在的收斂速度慢和容易陷入局部最優化的不足,提出一種采用變點交叉方式的多目標遺傳算法.我們發現,傳統的遺傳算法都以固定交叉點數進行交叉變異.但如果交叉點過少,起不到向最優解收斂的目的,而交叉點過多,收斂速度又會降低.
為在以上兩者之間找到平衡,本文設計了變點交叉的方式.運算初期采用多點交叉的方式,在于提高收斂速度.在運算后期逐步減少交叉點,直至采用兩點交叉、單點交叉的方式,避免丟失最優解導致早熟收斂.
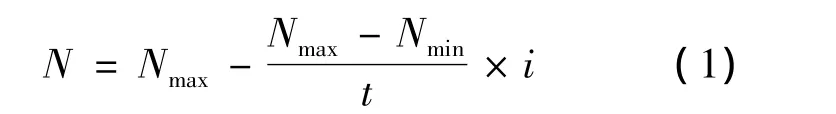
交叉點數:式中,Nmax是設定的最多交叉點數;Nmin是設定的最少交叉點數;t是本次運算所設定的變化間隔.這樣,在每個運算前期交叉點比較多,有很強的全局搜索能力.在中后期交叉點數比較少,可以防止局部優化,同時加快收斂速度.
圖1說明了4×4調度問題的變點交叉過程:第一代交叉點比較多,逐漸至最后一代為單點交叉.

圖1 變點交叉
1.2 多目標權衡分析,誘導交互權重
由于人的認知局限性和直覺模糊性,要直接確定決策者偏好關系是一件非常困難的事情[4].因為決策者在表達偏好時,往往只能對各目標的偏好程度提供主觀判斷,采用諸如“若保持其他目標不變,愿意用多少單位的目標A的性能損失換取多少單位目標B的性能改進”、“目標A比目標B重要”[5]等語言定性地表達兩兩目標的權衡關系,而不能給出精確的數學描述,因此多目標權衡分析采用一種間接的方法.
假設初始可行解集為 S*={S1,S2,S3,…,Sn},由代理值置換法[6]的思想,則其在目標i處相對目標j處的偏置換率可以近似為:
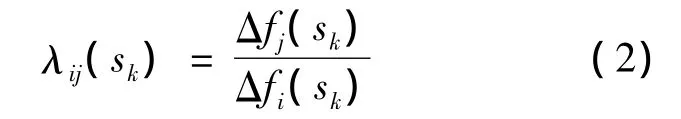
λij(sk)的含義為:在非劣可行解sk處,降低目標fi的性能一個單位,同時必須提高目標fj的性能λij(sk)個單位,從而使其他目標性能保持不變.
(1)通過與決策人的交互誘導出其偏好信息
通過人機界面向用戶提問:“保持其他目標不變的情況下,你愿意犧牲目標fi的多少個性能單位(kij(sk))以改進目標fj的性能?”,同時給出參考和限制,即:“若保持其他目標性能不變,降低目標fi的性能一個單位必須提高目標fj的性能λij(sk)個單位.”這說明了決策者能夠做出的讓步,表達出他在此方面的偏好.其中,0≤kij(sk)≤λij(sk).kij(sk)選擇參照表1.

表1 目標間相對重要程度的量化值
(2)將決策者隱性偏好轉換為顯性目標權重
由于目標之間的性能單位并不相同,具有不可比性,本文以目標的變化率即目標的相對數值來代替沒有意義的絕對數值,作為目標衡量的基準.
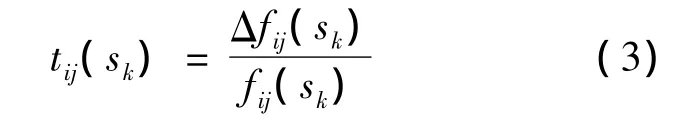
tij(sk)表示為在非劣解sk處,若保持目標i不變,目標j的變化率.
本文定義決策者的期望變化率為:
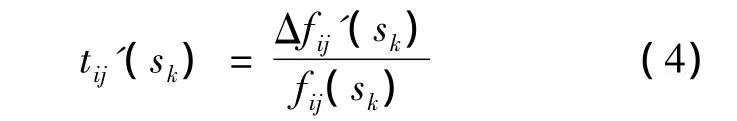
其中,Δf'ij(sk)=fij(sk)-kij(sk)
一般從人的思維習慣和心里狀態來講,決策者權衡目標兩兩利害關系的期望更理智和實際,也往往體現了他對該目標的關注程度[4].同樣由于目標單位的不可比性,以關注率(wij(sk))來表達決策者對目標的偏好.
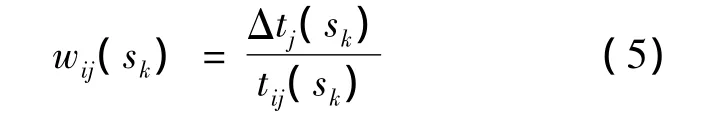
其中,Δtij(sk)=t'ij(sk)-tij(sk)
wij(sk)表示了在非劣解sk處,相對于目標i來講決策者對目標j的關注程度,即表達了決策者對于目標之間兩兩比較后的的偏好.
定義wii(sk)=1,根據線性平均法不難計算決策者的權重偏好.

整理后可得體現決策者目標偏好的權重wk,(k=1,2,…,i,…,j,…,n),同時滿足 wk> 0,
2 新的多目標遺傳算法流程
新算法流程如圖2所示,具體步驟如下:
Step1:針對車間調度的問題初始化參數,編碼采用文獻[7]Gen,Tsujimura和Kubota提出的基于工序的編碼方法;
Step2:給出至少一個用戶接受的可行解S(k);
Step3:通過人機交互,決策者對各目標兩兩權衡;
Step4:由公式(3)~(6),形成體現決策者主觀偏好的目標權重wi;
Step5:將個體的目標函數值作正規化處理;
Step6:計算個體適應度;
Step7:采用選擇、變點交叉、變異等遺傳算子產生一個子代種群;
Step8:世代更迭,若滿足結束條件則停止,否則轉向Step6;
Step9:輸出最優解.
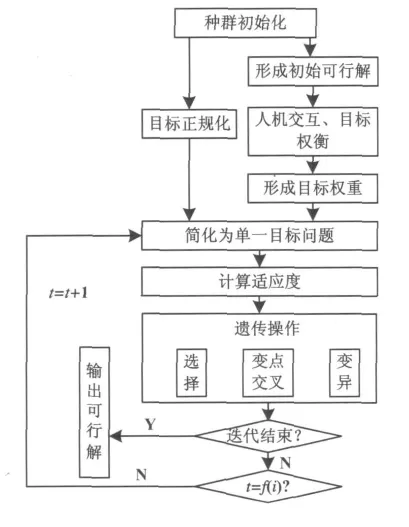
圖2 新的交互式多目標遺傳算法流程圖
3 算例分析
3.1 問題描述和參數選擇
本文對一個一般車間作業排序問題進行了研究,某車間有m臺機器,欲加工n種工件,每種工件的加工過程可由一系列工序組成,每道工序由相應的機器完成,每個工件在每臺機器上加工一次,每臺機器同時只能加工一個工件.其中m=10,n=10,并且以工件的最大完工時間和n個工件的平均延誤時間最小化為目標,其加工時間與調整時間均為區間[10,100]上生成的隨機數,交貨期為區間[500,1200]上生成的隨機數.新算法的基本參數的合理取值在表2中給出.
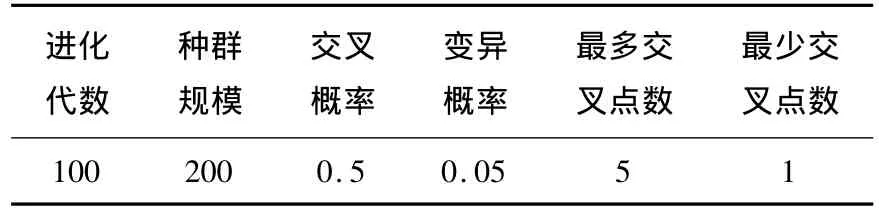
表2 新算法參數設置
以無偏好多目標優化的小生境Pareto遺傳算法(NPGA)結果作為對比,NPGA算法參數列在表3中.

表3 NPGA算法參數設置
3.2 優化結果分析
NPGA算法進化完成時,最終解的3/4都是Pareto最優解,而且分布極為廣泛,個體數目比較分散(圖3).讓決策者在眾多毫無側重點的可行解中進行選擇具有一定難度.圖4顯示了改進的多目標遺傳算法以平均延誤時間最小為偏好信息進化到相同代數后的個體分布情況.與NPGA算法相比,改進的多目標遺傳算法的個體向決策者偏好的方向集中,近60%的Pareto最優解集中在平均延誤時間在100~200的區域上.圖5是兩種算法的收斂曲線對比,明顯新算法的效率更高.
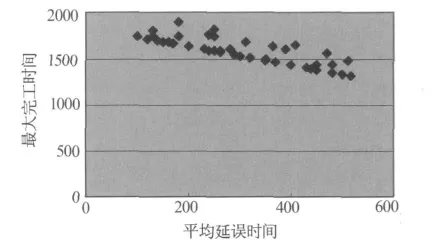
圖3 NPGA算法解的分布情況
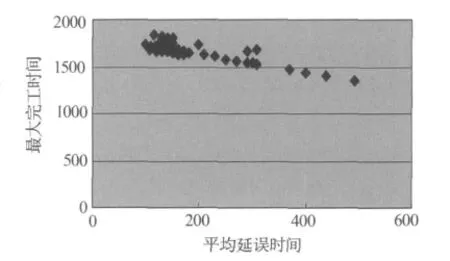
圖4 新算法解的分布情況
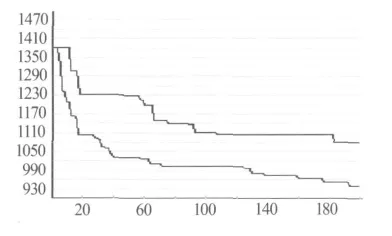
圖5 兩種算法收斂曲線對比
4 結論
(1)與NPGA相比,采用精英誘導目標權重的方式更好地考慮了多目標問題的決策者個人傾向,有效的簡化了作業排序的選擇過程.
(2)采用變點交叉的方式可防止局部收斂,加快運算速度;
綜上所述,改進的多目標遺傳算法適合于進行最佳作業排序方案的選擇,幫助管理者做出科學合理的決策,可有效地運用于作業車間調度問題.
[1]王凌.智能優化算法及其應用[M].北京:清華大學出版社,2001:131-170.
[2]周泓,張惠民.求解多目標作業排序問題的遺傳算法[J].系統工程理論與實踐,2008,8(8):1-8.
[3]CHANGKONG V,HAIMES Y Y.Multi-objective Decision Making:Theory and Methodology[M].New York:North-Holland,1983.
[4]申曉寧,郭毓,陳慶偉,等.一種引入偏好信息的多目標優化遺傳算法[J].信息與控制,2007,36(6):746-753.
[5]周熠.傾向型心態的表示和推理[D].合肥:中國科學技術大學,2006.
[6]古瑩奎,黃洪鐘,吳衛東.基于Pareto解的交互式模糊優化及其應用[J].清華大學學報(自然科學版),2009,44(8):1111-1114.
[7]曹先彬,王本年,王煦法.一種病毒進化型遺傳算法[J].小型微型計算機系統,2009,22(1):59-62.

