基于ATmega64L的128點實時FFT

郭 剛,李 釗,李建軍,胡禮勇,董巍巍

(1.第二炮兵青州士官學校,山東青州262500;2.第二炮兵駐石家莊地區軍事代表室,河北石家莊050081)

0 引言

目前,以單片機為核心的手持式振動信號采集器配有簡潔的信號調理和顯示電路,能夠完成低頻振動信號的采集、儲存和傳輸,成本低廉,在機器振動狀況檢測領域應用廣泛。但受單片機硬件資源的制約,其一般不具備現場對采樣數據進行FFT的能力[1,2]。然而,FFT是振動信號分析最常用的方法,對許多現場采集的信號數據,只需進行少量采樣點的FFT,即可算出機器振動的主頻,進而快速判斷運轉狀態,實現對機器運行狀態的快速檢測和故障初診,具有很大的實用價值。下面將著重闡述在以ATmega64L單片機為核心的手持式振動信號采集器上實現128點FFT的過程和方法。

1 按時間抽取基2FFT算法[3,4]

離散傅里葉變換(DFT)的本質就是建立了以時間為自變量的信號與以頻率為自變量的頻譜函數之間的變換關系。設X(n)為N點有限長序列,其DFT公式為:

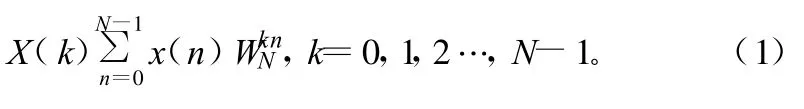
式中,

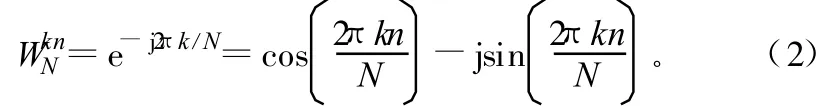
按時間抽取的基2FFT算法,利用旋轉因子的對稱性、周期性和可約性,根據輸入序列時間上的奇偶,將一個N點的DFT分解成2個N/2點的DFT,再把2個N/2點的DFT又可按照奇偶分成2個N/4的DFT,直到最終分解為N/2個2點的DFT運算。本算法的基本運算單元是2點蝶形運算結構。當N=2M時(這里M為自然數),整個運算共有M級,每級又有N/2個蝶形運算組成。蝶形運算計算流程如圖1所示。

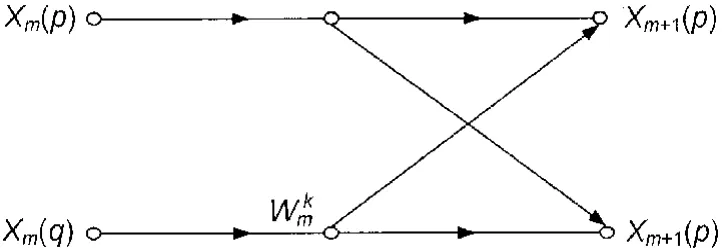
圖1 蝶形運算單元

蝶形運算方程式為:

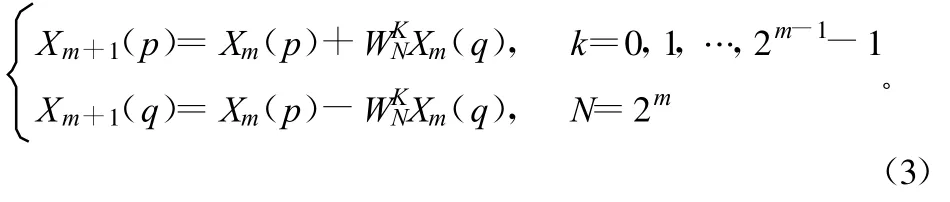
在處理采集到的實際數據時,輸入信號序列通常是實數。理論上使用N點復數FFT完成2N點實數序列FFT運算,可以提高運算速度并且減小存儲空間。但是變換完成后的結果轉化計算量較大,導致單片機整體運算速度不能顯著提高,又鑒于ATmega 64L單片機自帶 4 KB的 RAM,完全滿足128個32位浮點數進行FFT的存儲空間需求,所以此處直接使用128點復數FFT算法完成128個實數采樣數據的FFT運算,在運算時要把原實數數據作為復數的實部,而對應復數虛部需全部置零。

2 ATmega64L單片機采集系統

該系統采用ATmega64L單片機作為控制核心。它是基于RISC結構的8位低功耗CMOS微處理器,大部分指令都可以在一個時鐘周期內完成,最大可以支持16 MHz的系統時鐘,片載64 KB的可編程Flash,2B的EEPROM,4KB的SRAM,53個通用I/O口線,32個通用工作寄存器和2個串口、SPI接口和TWI接口等豐富的外圍接口電路。整個振動信號采集系統的硬件框圖如圖2所示。

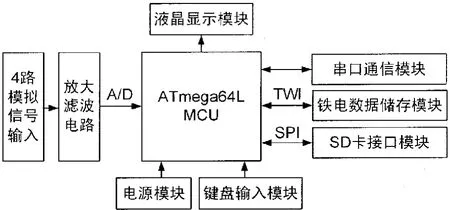
圖2 采集系統硬件

3 128點采樣數據實時FFT的實現

3.1 進行復數FFT計算的步驟及流程

使用ATmega64L單片機進行128點采樣數據FFT計算時,應首先把輸入的128個實信號虛部置零,使其變為復數,然后將數據序列按碼位倒置的方式反序排列,再進行按時間抽取基2FFT運算,最后計算轉換后各復數的模并比較分析振動信號主頻,具體FFT計算流程圖如圖3所示。

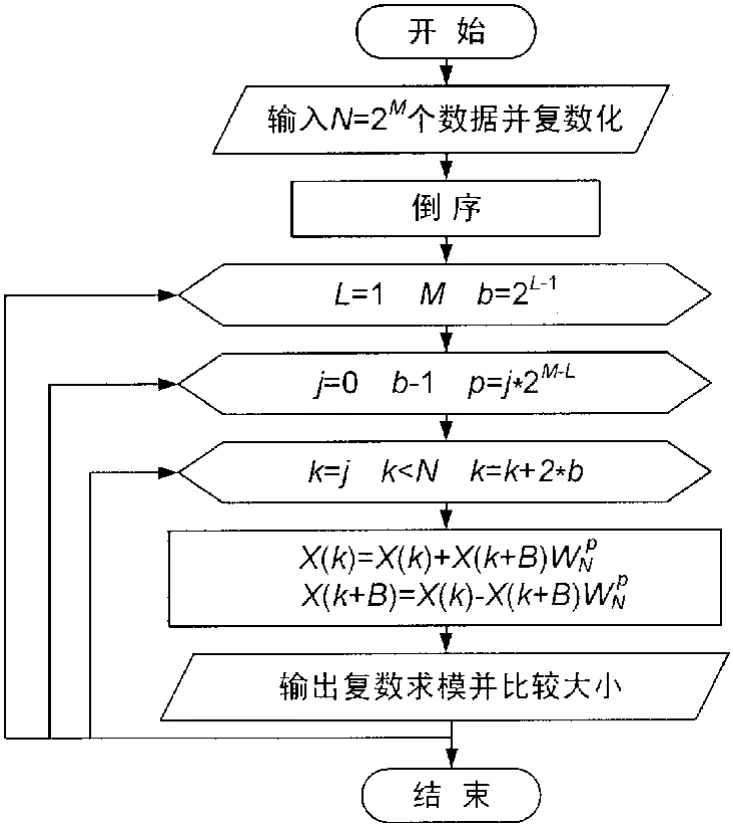
圖3 128點 FFT流程

3.2 在ICCAVR中編程實現FFT的要點

3.2.1 反序排列算法的實現

反序排列是由FFT算法的性質決定的。首先將128個數據點自然排列的十進制數轉換成7位二進制數,再將這些二進制數的首位至末尾的順序顛倒過來重新換算成十進制數,即得到反序排列的結果。為減小單片機的運算負擔,同時充分利用ATmega64L程序存儲器大的優勢,使用MATLAB軟件算出128點反序排列結果,并以數組形式存放在單片機程序存儲器中,FFT運算時,單片機只需進行簡單的查表,即可快速完成數據反序操作。單片機存儲128個序列碼為:

const unsigned char inv_tab[128]={0,64,32,96,16,80,……,47,111,31,95,63,127}。

3.2.2 旋轉因子的計算和儲存

進行FFT的子函數運算時,實時計算旋轉因子的值,對單片機而言是十分繁重的任務。根據旋轉因子的復數形式,預先算出 cos(2πkn/N)和sin(2πkn/N)的值(取小數點后4位精度),并以數組的形式存儲在單片機的程序存儲器內,供FFT運算過程中隨時調用。單片機存儲旋轉因子實部和虛部的形式為:

const float cos _tab[64]={0,-0.0491,-0.0980,-0.1467,…,-0.9808,-0.9892,-0.9952,-0.9988};

const float sin _tab[64]={1,0.9988,0.9952,…,-0.1467,-0.0980,-0.049}。

3.2.3 FFT各級蝶形運算的實現

根據FFT算法的特性,使用3級循環完成各級蝶形運算[5]。

for(L=1;L＜=7;L++){//L控制蝶形運算的級數

b=1;i=L-1;while(i＞0)

{b=b*2;i--;}//b控制蝶形運算2點之間的距離

for(j=0;j＜=b-1;j++)

{p=1;i=7-L;

while(i＞0)/*p=pow(2,7-L)*j;

{p=p*2;i--;}

p=p*j;//計算旋轉因子虛實部在數組中的對應序號p

for(k=j;k＜128;k=k+2*b)//完成本級N/2個蝶形運算

{TR=dataR[k];TI=dataI[k];temp=dataR[k+b];

dataR[k]=dataR[k]+dataR[k+b]*cos_tab[p]+dataI[k+b]*sin_tab[p];

dataI[k]=dataI[k]-dataR[k+b]*sin_tab[p]+dataI[k+b]*cos_tab[p];

dataR[k+b]=TR-dataR[k+b]*cos_tab[p]-dataI[k+b]*sin_tab[p];

dataI[k+b]=TI+temp*sin_ tab[p]-dataI[k+b]*cos_ tab[p];}

}

}

3.2.4 FFT結果的處理[6]

根據采樣定理,只要采樣頻率大于信號頻率的2倍,采樣得到的數字信號就可以做FFT變換了。N個采樣點經過FFT之后就可得到N個點的FFT結果。為了方便進行FFT運算,通常N取2的整數次方。假設采樣頻率為fs,信號頻率為f,采樣點數為N。那么FFT之后結果就是一個為N點的復數,每個點就對應有一個頻率點。這個點的模值就是該頻率值下的幅度,而每個點的相位就是該頻率下的信號的相位。FFT運算后第一個點表示直流分量(即0 Hz),第n個點所表示的頻率為:fn=(n-1)*fs/N。

4 實驗分析

為了驗證程序的正確性,使用手持式振動信號采集系統對FG1617函數波形信號發生器產生的標準9 Hz矩形波進行數據采集,采樣頻率設為128 Hz(該系統可以在10～1 000 Hz之間靈活設置采樣頻率)。然后截取采集到的128個連續數據點,使用Lab VIEW編制的專用FFT處理程序和ATmega64L內嵌的FFT程序分別進行分析,得到的幅頻結果如表1所示。

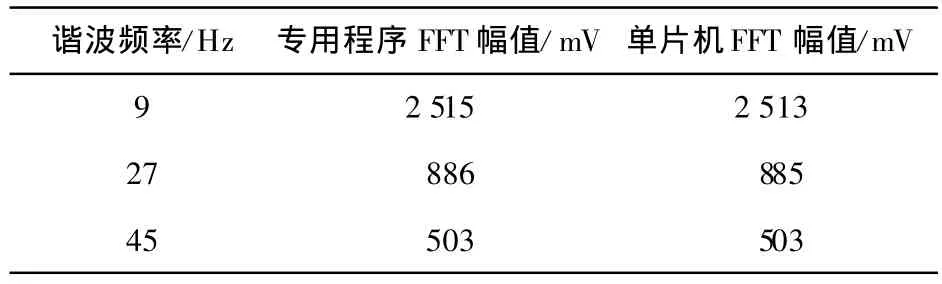
表1 FFT結果比較表

通過比較分析發現,ATmega64L單片機對128點采樣數據進行FFT,計算所得到的諧波主頻和幅值與使用專用數據處理程序計算得到的主頻和幅值基本吻合,達到設計要求精度。

5 結束語

FFT是信號采集領域的重要數據處理工具。上述充分利用高性能低成本的ATmega64L單片機硬件資源和高速運算能力,結合查表手段,可以在220 ms時間內完成128點的32位精度浮點FFT運算,而且經過實驗驗證轉換結果正確、精度夠用,證明了該型號單片機實現FFT運算的可行性,為FFT實現方法開辟了新的應用領域。在低成本手持振動信號采集儀器上集成FFT功能,通過對現場采集的振動信號進行實時FFT運算,算出被檢測機器的振動主頻和幅值,實現了對采樣數據的現場分析,滿足了設備運行狀態檢測和故障初判的要求。

[1]肖 飛.手持式振動測試系統的軟件開發[D].南京:東南大學,2005:1-5.

[2]賈民平,劉玉春,鐘秉林,等.便攜式數據采集與工況監測分析系統的研制[J].東南大學學大報,1997,27(2):99-102.

[3]胡廣書.數字信號處理—理論、算法與實現[M].北京:清華大學出版社,2003:177-198.

[4]文其林,白曉東,周 洪,等.2048點FFT在TMS320C240x定點DSP上的實現[J].微計算機信息,2006(5-2):159-160.

[5]肖宛昂.嵌人式系統中FFT算法研究[J].單片機與嵌入式系統應用,2003(1):69-71.

[6]李全利,劉長亮.CCS上FFT運算的實現[J].自動化技術____與應用,2009,28(2):61-63.