智能PI算法在永磁同步電動(dòng)機(jī)控制系統(tǒng)中的應(yīng)用

郭衛(wèi)杰，劉維亭，林永才

(1.江蘇科技大學(xué)，江蘇鎮(zhèn)江212003;2.張家港合豐機(jī)械制造有限公司，江蘇蘇州215618)

0 引 言

當(dāng)前應(yīng)用在永磁同步電動(dòng)機(jī)(PMSM)控制系統(tǒng)中的轉(zhuǎn)速調(diào)節(jié)器是傳統(tǒng)PI調(diào)節(jié)器，雖然具有結(jié)構(gòu)簡(jiǎn)單的特點(diǎn)，但是用固定的參數(shù)處理PMSM系統(tǒng)完整的運(yùn)行過(guò)程，難以實(shí)現(xiàn)較好的動(dòng)態(tài)性能。

智能PI算法具有較強(qiáng)的自適應(yīng)性，控制算法不依賴于對(duì)象模型，能夠動(dòng)態(tài)地改變控制器的結(jié)構(gòu)和參數(shù)，具有較強(qiáng)的魯棒性［1］。應(yīng)用智能PI調(diào)節(jié)器作為PMSM控制系統(tǒng)的轉(zhuǎn)速調(diào)節(jié)器，可以提升整個(gè)系統(tǒng)的動(dòng)態(tài)性能。

本文在MATLAB平臺(tái)上應(yīng)用SVPWM算法，搭建永磁同步電動(dòng)機(jī)矢量控制系統(tǒng)的模型，對(duì)傳統(tǒng)PI轉(zhuǎn)速調(diào)節(jié)器、智能PI轉(zhuǎn)速調(diào)節(jié)器的控制系統(tǒng)進(jìn)行仿真對(duì)比，仿真結(jié)果表明智能PI調(diào)節(jié)器控制系統(tǒng)的整體性能優(yōu)于傳統(tǒng)PI調(diào)節(jié)器控制系統(tǒng)的性能。

1 控制系統(tǒng)模型的建立

在MATLAB的Simulink環(huán)境下，利用其豐富的模塊庫(kù)，搭建一個(gè)完整的矢量控制系統(tǒng)。整個(gè)控制系統(tǒng)包括逆變橋與PMSM模塊、坐標(biāo)變換模塊、速度和電流的PI調(diào)節(jié)器模塊、SVPWM模塊等模塊。

1.1 逆變橋與PMSM模塊

逆變橋采用由6個(gè)IGBT組成的3相橋電路模塊。PMSM模塊有4個(gè)輸入端，1個(gè)輸出端，其中A、B、C是三相定子繞組輸入端，Tm是負(fù)載轉(zhuǎn)矩，輸出端m輸出電機(jī)的定子電流、電磁轉(zhuǎn)矩、轉(zhuǎn)子轉(zhuǎn)速、轉(zhuǎn)子位置等。

1.2 坐標(biāo)變換模塊

系統(tǒng)模型中所用到的坐標(biāo)變換有Clarke變換、Park變換和Park－1變換。仿真模型中需要將定子電流ia、ib、ic變換為id、iq，也就是 Clarke+Park 變換，變換模塊如圖1所示，Park－1變換也按此方法設(shè)計(jì)。

圖1 Clarke+Park變換

1.3 速度、電流的PI調(diào)節(jié)器模塊

在PMSM控制系統(tǒng)中，傳統(tǒng)轉(zhuǎn)速PI調(diào)節(jié)器模型如圖2所示。電流PI調(diào)節(jié)器按照此模型設(shè)計(jì)。

1.4 SVPWM 模塊

1.4.1 SVPWM 算法原理

三相電壓型逆變器共有八種不同的開(kāi)關(guān)狀態(tài)(000、001、010、011、100、101、110、111，上下橋臂不能同時(shí)導(dǎo)通，1表示上橋臂導(dǎo)通，0表示下橋臂導(dǎo)通)，其對(duì)應(yīng)有八種不同的電壓矢量。其中000、111對(duì)應(yīng)零電壓矢量，其余6種開(kāi)關(guān)狀態(tài)對(duì)應(yīng)非零電壓矢量u1～u6，6個(gè)非零電壓矢量的模都等于，則可以構(gòu)成一個(gè)等邊六邊形，并劃分為6個(gè)扇區(qū)，零電壓矢量位于坐標(biāo)O點(diǎn)［2］。如圖3所示。

圖2 轉(zhuǎn)速PI調(diào)節(jié)器

圖3 電壓空間矢量圖

在電壓空間矢量圖上建立r1、r2、r3坐標(biāo)系，根據(jù)它們的關(guān)系判斷扇區(qū)。定義:

當(dāng)r1＞0時(shí)，令A(yù)=1;當(dāng)r2＞0時(shí)，令B=1;當(dāng)r3＞0時(shí)，令C=1，取N=A+2B+4C［3］，則可得到N與各扇區(qū)的對(duì)應(yīng)關(guān)系，如表1所示。

表1 N與扇區(qū)號(hào)關(guān)系

對(duì)于任意空間電壓矢量us，假設(shè)位于第Ⅰ扇區(qū)，把它沿相鄰的兩個(gè)空間矢量u1、u2的方向分解成兩個(gè)分量uref1、uref2，根據(jù)平均值等效原理，設(shè)PWM的周期為T(mén)s，uref1作用時(shí)間為T(mén)1，uref2作用時(shí)間為T(mén)2，零電壓矢量作用時(shí)間為T(mén)0，可得:

空間電壓矢量us在αβ坐標(biāo)系上的投影為uα、uβ［4］，那么可列式:

計(jì)算得出:

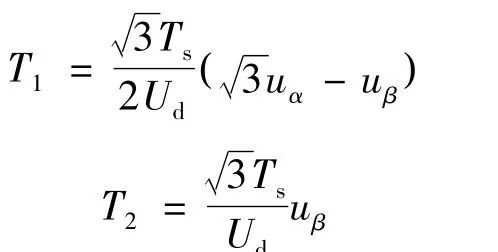
定義X、Y、Z如下:

那么N與相應(yīng)矢量的作用時(shí)間的關(guān)系如表2所示。

表2 N與矢量作用時(shí)間關(guān)系

T1、T2賦值后，再進(jìn)行飽和判斷，當(dāng)T1+T2＞Ts時(shí)，T1=T1Ts/(T1+T2)，T2=T2Ts/(T1+T2)。最后再進(jìn)行切換點(diǎn)計(jì)算。T=T ba則N與比較器切換點(diǎn)的關(guān)系如表3所示。

表3 N與比較器切換點(diǎn)關(guān)系

1.4.2 SVPWM 模型建立SVPWM模型如圖4所示。

圖4 SVPWM模型

1.5 永磁同步電動(dòng)機(jī)控制系統(tǒng)模型的建立控制系統(tǒng)模型如圖5所示。

2 仿真參數(shù)設(shè)置

本系統(tǒng)的永磁同步電動(dòng)機(jī)參數(shù):定子電阻Rs=4.765 Ω，交、直軸的電感Lq=Ld=0.014 H，轉(zhuǎn)子磁鏈 0.184 8 Wb，轉(zhuǎn)動(dòng)慣量J=0.000 105 1 kg·m2，極對(duì)數(shù)p=2。

功率器件IGBT開(kāi)關(guān)頻率為10 kHz，仿真時(shí)間為0.08 s，給定轉(zhuǎn)速為1 000 r/min，電機(jī)空載起動(dòng)，在t=0.03 s時(shí)突加負(fù)載Tm=1 N·m。在此條件下得到的仿真波形如圖6所示。

圖5 永磁同步電動(dòng)機(jī)矢量控制系統(tǒng)模型

圖6 傳統(tǒng)PI轉(zhuǎn)速調(diào)節(jié)器下的仿真波形

由轉(zhuǎn)速仿真圖6b可看出，轉(zhuǎn)速超調(diào)現(xiàn)象比較明顯，在t=0.03 s時(shí)電機(jī)突加負(fù)載，電機(jī)轉(zhuǎn)子轉(zhuǎn)速回到給定值的時(shí)間較長(zhǎng);由定子電流和轉(zhuǎn)子轉(zhuǎn)矩仿真圖6a、圖6c可看出，電機(jī)起動(dòng)時(shí)，定子電流和電磁轉(zhuǎn)矩較大，較大的沖擊電流和轉(zhuǎn)矩對(duì)電機(jī)的損傷比較大。所以需要引入更合理的算法改進(jìn)這些不足。

3 智能PI調(diào)節(jié)器

3.1 智能PI調(diào)節(jié)器的原理與結(jié)構(gòu)

轉(zhuǎn)速的偏差、偏差的微分、偏差的積分分別代表系統(tǒng)輸出的當(dāng)前、將來(lái)和過(guò)去三種狀態(tài)。智能型PI調(diào)節(jié)器結(jié)構(gòu)如圖7所示，x1為轉(zhuǎn)速偏差，x1=e;x2為轉(zhuǎn)速偏差的積分，x2=∫edt;x3為實(shí)際轉(zhuǎn)速的負(fù)微分系統(tǒng)根據(jù)這三個(gè)值確定的區(qū)間確定相應(yīng)的規(guī)則。當(dāng)偏差較大時(shí)，去掉積分環(huán)節(jié)并調(diào)整比例系數(shù)KP，使系統(tǒng)以最大的能力消除偏差;當(dāng)偏差較小時(shí)，投入積分環(huán)節(jié)并在線實(shí)時(shí)調(diào)整比例系數(shù)KP和積分系數(shù)KI，使系統(tǒng)以最佳過(guò)程達(dá)到穩(wěn)態(tài)［1］。

圖7 智能PI調(diào)節(jié)器的結(jié)構(gòu)圖

3.2 參數(shù)調(diào)整規(guī)則

(1)當(dāng)x1＞m，m=(10%～20%)n時(shí)，說(shuō)明誤差很大，這時(shí)只保留比例部分去掉積分部分，調(diào)整，使誤差以允許的最大速度減小。此時(shí)，它相當(dāng)于實(shí)施開(kāi)環(huán)控制。

(2) 當(dāng)x1＜m，x1x3＜0時(shí)，此時(shí)x1＞0、x3＜0或x1＜0、x3＞0，表明偏差正在趨近于零，應(yīng)該削弱比例部分的控制作用，逐步減小KP。

由于KI＞0，故控制器輸出的積分部分KIx2與x2同號(hào)，當(dāng)x2＞0、x1＞0時(shí)，積分部分產(chǎn)生加速轉(zhuǎn)矩，以減小偏差;而x2＜0、x1＜0時(shí)，產(chǎn)生制動(dòng)轉(zhuǎn)矩，使得實(shí)際轉(zhuǎn)速趨近于給定值。因此，當(dāng)x1x2＞0時(shí)，積分部分有利于消除偏差，應(yīng)增大KI。反之，當(dāng)x1x2＜0時(shí)，積分部分使偏差的絕對(duì)值增大，應(yīng)減小KI［5］。

參數(shù)調(diào)整規(guī)則:

(3) 當(dāng)x1＜m，x1x3＞0時(shí)，此時(shí)x1＞0、x3＞0或x1＜0、x3＜0時(shí)，說(shuō)明速度偏差在增大，應(yīng)該迅速增大KP，使x3盡快反號(hào)，快速地減小速度偏差。偏差離零越遠(yuǎn)，且離開(kāi)速度越來(lái)越快時(shí)，KP增大得越快。KI的調(diào)整規(guī)則與x1x3＜0時(shí)相同。

參數(shù)調(diào)整規(guī)則為:

(4)當(dāng)x1＜m，x1x3=0時(shí)，系統(tǒng)在平衡點(diǎn)運(yùn)行，保持KP、KI不變。

轉(zhuǎn)速PI調(diào)節(jié)器更新模型如圖8所示。

圖8 智能PI調(diào)節(jié)器模型

3.3 引入智能PI調(diào)節(jié)器的系統(tǒng)仿真

系統(tǒng)其它仿真參數(shù)不變，給定轉(zhuǎn)速為1 000 r/min，電機(jī)空載起動(dòng)，在t=0.03 s時(shí)突加負(fù)載Tm=1 N·m。仿真波形如圖9所示。

圖9 智能PI轉(zhuǎn)速調(diào)節(jié)器的仿真波形

對(duì)比兩種仿真結(jié)果，使用智能PI算法的永磁同步電動(dòng)機(jī)矢量控制系統(tǒng)，起動(dòng)時(shí)定子電流和電磁轉(zhuǎn)矩明顯減小，轉(zhuǎn)子轉(zhuǎn)速無(wú)明顯超調(diào)，上升時(shí)間也較短;突加負(fù)載轉(zhuǎn)矩?cái)_動(dòng)后，動(dòng)態(tài)速降和恢復(fù)時(shí)間均小于使用傳統(tǒng)PI調(diào)節(jié)器的控制系統(tǒng)。

仿真結(jié)果證明了智能PI調(diào)節(jié)器應(yīng)用在永磁同步電動(dòng)機(jī)控制系統(tǒng)中的可行性。系統(tǒng)的起動(dòng)特性、抗干擾能力均優(yōu)于使用傳統(tǒng)PI調(diào)節(jié)器。

4 結(jié) 語(yǔ)

智能PI算法不依賴控制模型，它根據(jù)當(dāng)前系統(tǒng)的運(yùn)行狀態(tài)，動(dòng)態(tài)地改變控制器的結(jié)構(gòu)和參數(shù)，有較強(qiáng)的魯棒性。在永磁同步電動(dòng)機(jī)矢量控制系統(tǒng)中應(yīng)用智能PI調(diào)節(jié)器作為轉(zhuǎn)速調(diào)節(jié)器，系統(tǒng)的響應(yīng)速度快、超調(diào)量小、動(dòng)態(tài)性能優(yōu)良。

這種基于智能PI調(diào)節(jié)器的永磁同步電動(dòng)機(jī)控制系統(tǒng)，其調(diào)整規(guī)則少，計(jì)算量小，容易在實(shí)際的系統(tǒng)中實(shí)現(xiàn)，有著良好的應(yīng)用價(jià)值。

［1]陳伯時(shí).電力拖動(dòng)自動(dòng)控制系統(tǒng)［M］.北京:機(jī)械工業(yè)出版社，2006.

［2]陸海峰，瞿文龍，張磊，等.基于調(diào)制函數(shù)的SVPWM算法［J］.電工技術(shù)學(xué)報(bào)，2008，23(2):37－43.

［3]龔云飛，富歷新.基于Matlab的永磁同步電機(jī)矢量控制系統(tǒng)的仿真研究［J］.微電機(jī)，2007，40(2):33－36.

［4]祝恩國(guó)，鄒和平，趙兵，等.基于TMS320F2812的SVPWM算法分析與實(shí)現(xiàn)［J］.微電機(jī)，2008，41(4):36－38.

［5]阮毅，徐靜，陳伯時(shí).智能PI控制在交流調(diào)速系統(tǒng)中的應(yīng)用［J］.電工技術(shù)學(xué)報(bào)，2005，20(3):80－84.