基于逆系統的雙饋變速恒頻發電機組的控制研究

張繼勇，張蘇新，卞皓瑋

(揚州大學，江蘇揚州225009)

0 引 言

風能是比較廉價和有很好發展前景的一種新能源?，F在世界很多國家都很重視對于風能的開發利用，在風力發電領域變速恒頻發電系統已是一種主流，尤其對于雙饋感應電機的利用尤為突出。

由于風力發電機是強耦合，多變量的非線性機電系統，經典控制難以滿足系統的控制精度及動態性能要求。目前多采用基于矢量控制系統的策略，網側采用了電網電壓定向矢量控制［3－4］，機側則采用了定子磁場定向。但仍存在一些問題:(1)對擾動及其參數變化較敏感;(2)對直流母線電壓的恒定和單位功率因數控制的穩定性并不是很好。

逆系統方法是一種非線性系統反饋線性化控制的新理論，該方法物理概念清晰，適用面廣，應用簡便，已成功應用于一些系統控制。文獻［5，7］針對矢量控制存在的一些問題，提出了一種逆系統方法，為分析和設計風力發電網側變換器控制提供了便利。本文采用基于逆系統方法來控制雙饋風力發電系統，并進行了計算機仿真。仿真結果表明該控制系統具有較好的穩定性能和動態性能。

1 DFIG及網側變換器模型

1.1 DFIG風力發電系統結構

DFIG發電系統基本結構如圖1所示。

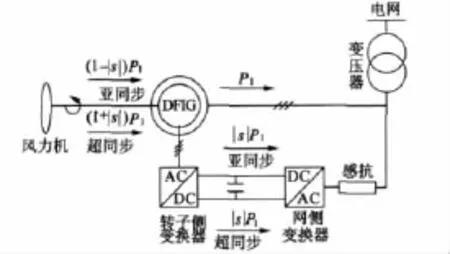
圖1 DFIG風力發電基本結構圖

對于風力發電的雙饋電機來說，主要運行于亞同步和超同步速狀態，功率流向如圖1所示。系統包含雙PWM變換器，即網側和轉子側變換器。

1.2 雙饋風力發電網側變換器數學模型

變速恒頻風力發電系統要求網側變換器控制直流母線電壓穩定，保持單位功率因數，并且實現有功和無功功率的解耦。為了實現三相PWM變換器的高性能控制，首先需要建立并分析它的數學模型，通過坐標變換轉化為dq坐標系下的數學表達式。圖2為三相PWM變換器網側拓撲結構圖。

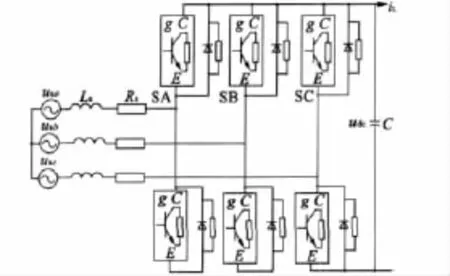
圖2 網側變流器結構

根據圖2，在abc坐標系下的數學模型，再根據坐標變換原理，實現abc到dq坐標變換，可得三相電壓型PWM變換器在dq坐標系下的數學模型:

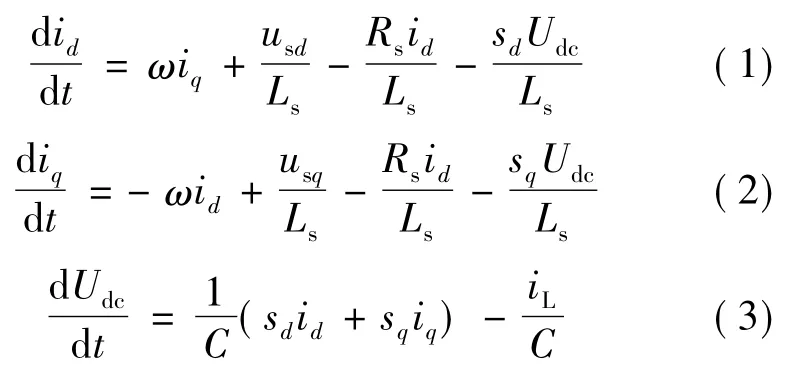
在dq坐標系下，輸入的復功率為:

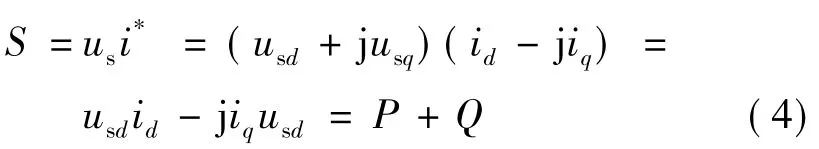
由式(5)可知，網側變換器的有功功率和無功功率分別由id和iq控制:

2 DFIG網側變換器逆系統控制結構

所謂逆系統控制方法就是通過構造可實現的α階逆系統將原系統補償成為具有線性傳遞關系的且已解耦的偽線性復合系統，然后對已線性化的系統或線性化解耦的各子系統設計閉環控制器，形成復合控制器(復合控制系統)的控制方法，如圖3所示。

根據上述推導可選取系統狀態變量:

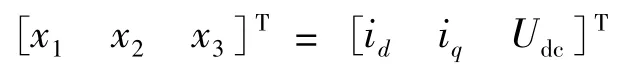
選取輸出變量:

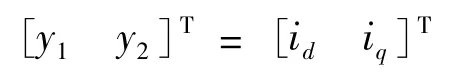
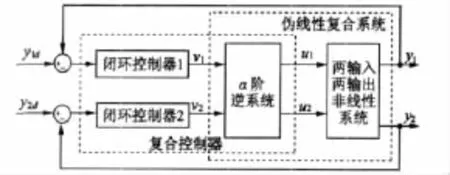
圖3 由α階逆系統與閉環控制器構成的復合控制器

選取輸入變量:

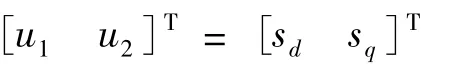
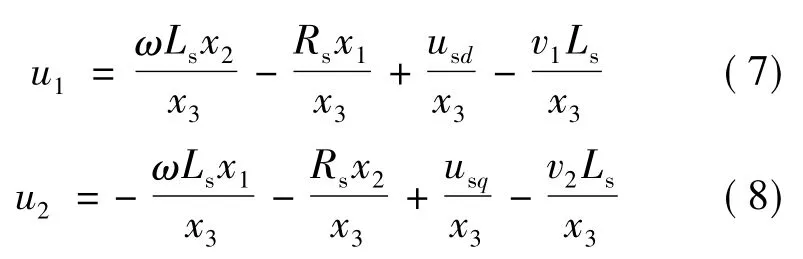
三相網側PWM變換器控制系統的目標是:使系統電流電壓同相位，即單位功率因數，且直流母線電壓恒定，根據上述條件，系統在穩態時，可以令:

代入式(1)～式(3)并化簡:

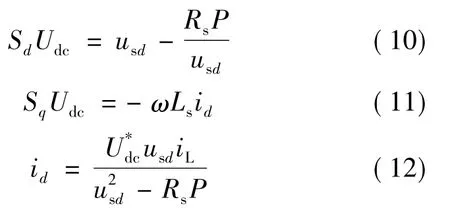
當Rs較小時可將其忽略，則id的穩態值:

為了消除系統濾波電阻Rs的影響，消除直流電，:壓穩態誤差 將 修改

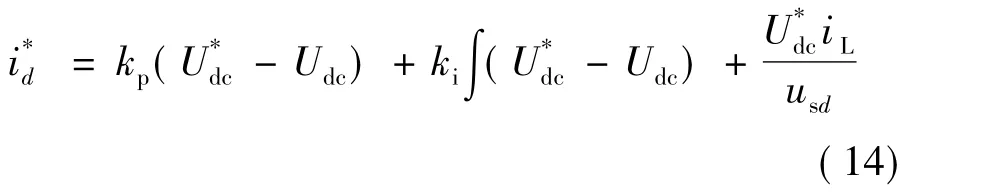
閉環控制器可以通過傳遞函數來求取。設傳遞函數:

為了實現其傳遞函數，變換控制系統的表達式:

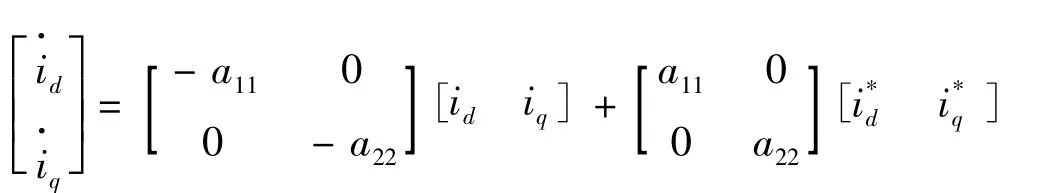
上式表明系統的輸出可以通過傳遞函數G(s)追蹤系統的輸入。如果輸入取參考值，那么期望的電流輸出就能取得。系統控制結構圖如圖4所示。

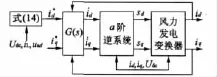
圖4 系統控制框圖

3 控制系統的結構

本文設計的基于逆系統的結構如圖5所示。

圖5 基于逆系統控制方法的系統結構圖

用電壓、電流傳感器測得的數值進行運算，得到有功無功功率。圖中變換的角度可以通過角度檢測器檢測。SVPWM模塊為電壓空間矢量模塊，控制變流器六個橋的導通或關斷。該模塊的使用使變流橋開關頻率恒定，便于交流側濾波電感的設計。

4 仿真驗證

為了驗證本文提出的偽線性逆系統控制方案的正確性，本文使用Matlab/Simulink軟件對控制系統進行了仿真。仿真參數為:雙饋電機額定功率2.5 kW，定子電阻0.435Ω，轉子漏感2 mH，轉子電阻0.816 Ω，轉子漏感 69.31 mH，轉動慣量 0.089 kg/m2;網側交流電壓有效值75 V，直流母線電壓140 V，進線電阻Rs=0.05Ω，進線電感Ls=6 mH，直流母線電容C=2 200μF。

當DFIG穩定運行時，定子側向電網輸出的有功功率一定，根據最大功率捕捉和功率平衡，當風力機輸入功率發生變化時，變換器功率也發生變化。如果風速減小使轉差率變為原來的兩倍，則變換器向風機提供的有功功率|S|P1增大到原來的兩倍。

圖6a為直流母線電壓圖。在0.2 s前，發電機處于穩定狀態時，直流母線電壓穩定。0.2 s后風速減小有功功率增加，母線電壓有所波動。但過段時間后電壓又保持恒定，實現了直流母線電壓的穩定。

圖6b為相電壓相電流的仿真圖，電壓與電流同相位，實現了交流側單位功率因數，在0.2 s時有功功率增加一倍，相電流近似為原來的兩倍。

圖6c～圖6f分別為無功功率、有功功率、功率因數和相電流頻譜的仿真圖，從圖中可以看出，實現了無功和有功的解耦，無功功率在有功功率變化時依然等于零，且能維持單位功率因數，且諧波分量非常小。仿真結果可以看出該控制方法具有較好的動態穩定性。

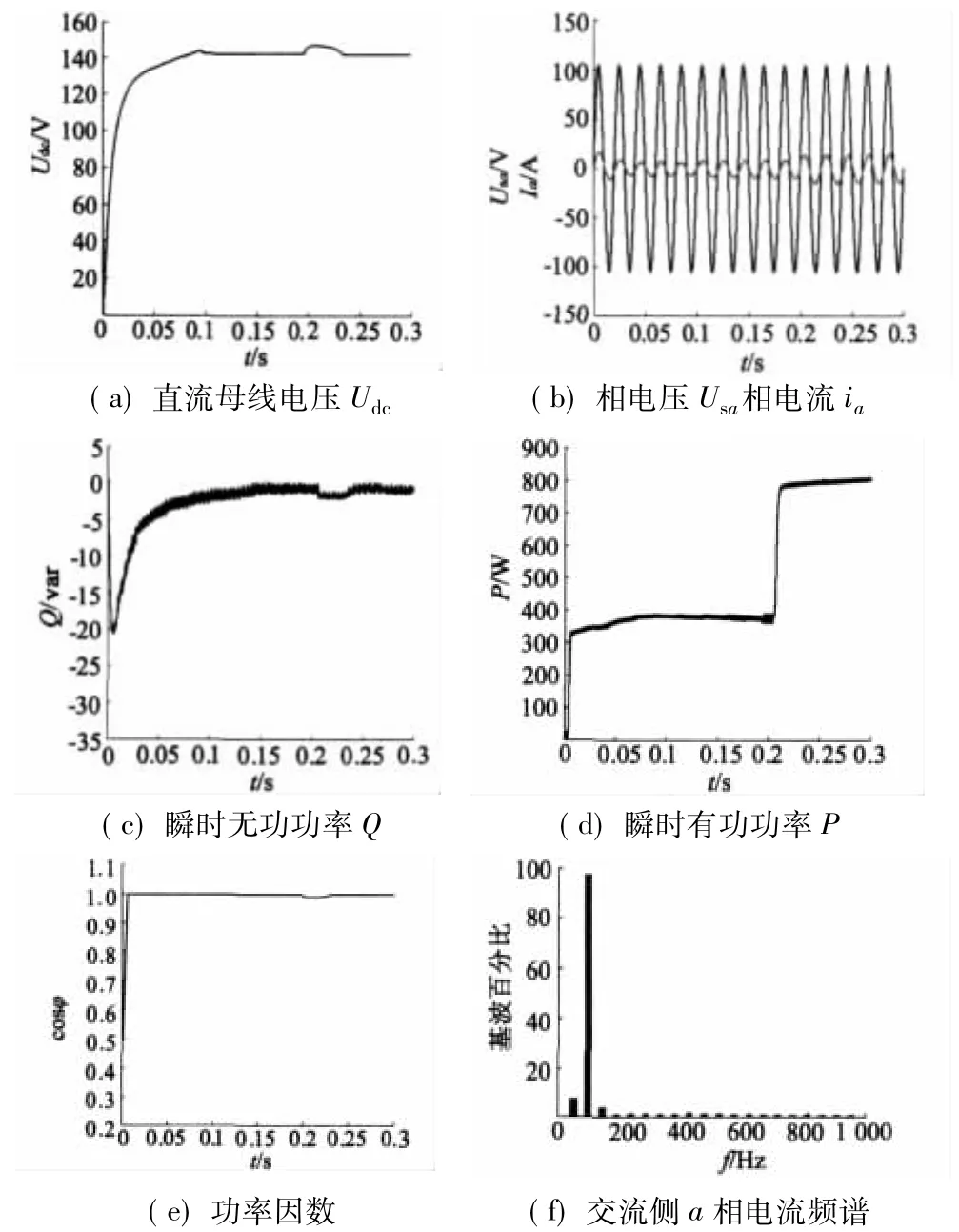
圖6 轉子輸入電能有功功率增加，逆系統仿真波形

圖7a、圖7b分別為A相電壓在0.25 s跌落10%時，A相電壓及電流和直流母線電壓的仿真圖，并且相電壓在0.3 s恢復。從圖中可以看出，電壓跌落時，相電流增加，但依然能保持同相位，而直流母線電壓有所波動，一段時間后直流母線電壓仍能穩定。仿真結果表明該控制方法具有較好的動態穩定性。

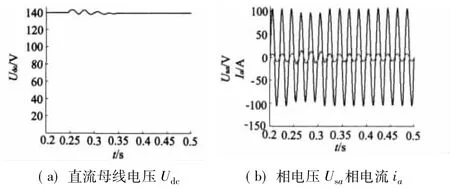
圖7 A相電壓在0.25 s跌落10%時逆系統仿真模型

5 結 語

本文在變速恒頻風力發電網側變換器數學模型的基礎上，通過逆系統理論及控制模型，構造了偽線性控制系統，通過dq電流的解耦控制，實現了有功無功功率的解耦，利用閉環控制器控制提高了系統的穩定性，通過Matlab/Simulink仿真對所提出的控制方法進行了驗證，仿真結果表明本文所提出的偽線性逆系統控制策略具有較好的動態性和穩定性。

［1]李春文，馮元坤.多變量非線性控制的逆系統［M］.北京:清華大學出版社，1991.

［2]王兆安，黃俊.電力電子技術［M］.北京:機械工業出版社，2000.

［3]林渭勛.現代電力電子技術［M］.北京:機械工業出版社，2007.

［4]陳伯時.電力拖動自動控制系統－運動控制系統(第3版)［M］.北京:機械工業出版社，2003.

［5]戴先中，劉國海，張興華.交流傳動神經網絡逆控制［M］.北京:機械工業出版社，2007.

［6]張崇魏，張興.PWM整流器及其控制［M］.北京:機械工業出版社，2003.

［7]李泰，王奔.基于逆系統方法的三相PWM整流器直接功率控制［J］.電氣傳動，2008，38(10):33－38.

［8]Trzynadlowski A M，Legowaki S F.Minimum－loss Vector PWM Strategy for Three－phase Inverters［J］.IEEE Trans.Power Electron，1994，9(2):26－34.

［9]Jie F，Huang J.Novel Modulation Method for Direct Power Control of Three－phase PWM Rectifier［J］.Power Electronics，2006，40(4):9－11.

［10]Sira Ramire H.Nolinear P－I controller design for switchmode DC－to－DC power converters［J］.IEEE Trans.Circuit Syst.，1991，38(4):410－417.

［11]Pena R，Clare JC，Asher GM.Doubly fed induction generation using back－to－back PWM converters and its application to variable speed wind energy generation［J］.IEEE Proceedings－Electric Power Applications，1996，143(3):231－241.

［12]Rioual P，Poliquen H，Louis J P.Non－linear control of PWM rectifier by feedback linearization and exact PWM control［C］//Conf.Rec.IEEE PESC＇94，1994:1095－1102.

［13]Leithead W E，Salle SD，Reardon D.Role and objictives of control for wind turbines［J］.IEEE Proc.Part.C，1991:135－148.

［14]Chedid R.Intelligent Control for Wind Energy Conversion Systems［J］.Wind Engineering，1998，22(1):1－16.

［15]Ackermann T，Soder L.An overview of wind energy－status 2002［J］.Renewable and Sustainable Energy Reviews，2002，6(1－2):67－127.

［16]Lee T S.Nolinear state feedback control design for three－phase PWM boost rectifiers using extended linearization［J］.IEEE Proc.Power Appl.，2003:546－554.