單邊直線感應電動機直接推力控制方法研究
易一鵬,莊圣賢,周志超,程遠銀
(西南交通大學,四川成都610031)
0 引 言
直線電動機具有非粘著驅動牽引方式、調速性能穩定、加速快、噪聲低、重量輕等優點。直線感應電動機作為其中重要的一個分支,近年來在工業和交通等領域的研究及應用中備受重視。如高速運載系統、滑動門、電梯、火箭發射裝置等等[1]。
直線感應電動機(以下簡稱LIM)采用長直的兩端開斷結構,當初次級發生相對運動時,因縱向和橫向邊緣效應引起氣隙磁場畸變,使得電機效率降低,因此其等效電路模型不像旋轉感應電機那樣簡單[2]。磁場對電機控制性能的好壞起著決定性作用,因而分析其數學模型非常重要。經典的矢量控制和空間矢量調制方法已經被廣泛應用于控制LIM[2]中,相對而言,響應速度快、控制方式簡單的直接轉矩控制方法在LIM控制上的研究近年來才興起。文獻[3]建立了靜止參考坐標系下的LIM模型并應用了直接推力控制方法,但其模型是基于轉子磁場定向而建立的。文獻[4-5]從電機的不對稱結構出發,應用直接轉矩控制方法控制LIM,但在構建電機模型時,未把邊緣效應的影響量化到等效模型中。本文建立了直線感應電動機靜止坐標系下的數學模型,并基于Matlab/Simulink對該模型進行了直接推力控制仿真,仿真結果說明了邊緣效應對LIM的運行性能影響很大,同時驗證了電機模型和控制策略的正確性和有效性。
1 LIM模型分析
直線電動機可以看作為將普通的旋轉電機沿軸線方向的平面剖開然后展開成直線形狀而成[1]。對于短初級長次級單邊LIM,其初級與旋轉感應電機的定子繞組相對應,次級與轉子繞組對應[2]。
由于這種特殊的結構,直線電動機在運行時會產生數種邊緣效應[1]。其中橫向邊緣效應可以通過初、次級寬度的調整得到改善;靜態縱向邊緣效應可以通過各相繞組之間的換位或者增加極對數的方法得到改善[6];但是動態縱向邊緣效應的影響很大,在高速時尤為明顯。
圖1為短初級長次級的LIM模型。當電機初級以速度v運動時,某部分次級導體進入到初級下的氣隙中,由于氣隙磁鏈守恒,次級導體板閉合回路中除了產生與通常旋轉電機中同樣的感應電動勢和電流外,還存在著由于閉合回路磁通發生變化而引起的感應渦流,這種感應電流會削弱氣隙中的磁場;同樣地,當次級導體板在離開初級時也會產生一種感應電流,這種感應電流加強氣隙中的磁場。根據Duncan的理論,引入無單位量綱Q來修正旋轉異步電動機模型,使邊緣效應的影響量化入等效電路中[7],無單位量綱Q定義:


圖1 直線電機初級以速度v運動時在進入端和離開端產生渦流
式中:D表示電機的初級長度;R表示次級電阻;v表示電機直線速度;Llr表示次級漏感;Lm表示勵磁電感。在電機參數一定時,其大小取決于速度。若速度為零時,則Q為無限長,邊緣效應便可忽略。而隨著速度的上升,該值就減小,LIM的勵磁電流也減小,邊緣效應的影響就會變大。
次級端部渦流損耗可以等效為在d軸勵磁回路中串聯一個的電阻。次級渦流的去磁作用可以等效為一個去磁電感,然后與原有勵磁電感并聯,得總勵磁電感設邊緣效應函數即總勵磁電感:

在轉子磁場定向矢量控制方法中,由于ψrd=|ψr|,ψrq=0,邊緣效應對q軸磁鏈沒有影響,可認為LIM的q軸電路與普通旋轉感應電機q軸電路一樣。在直接推力控制方法中,采用保持定子磁鏈恒定的方法,即:,邊緣效應對d、q軸磁鏈均有影響。結合G.Kang的LIM模型[8]與異步電動機動態等效電路[9],由上分析可得直線感應電動機在靜止坐標系下的等效電路,如圖2所示。

圖2 直線感應電動機d-q等效電路
2 LIM方程的建立
根據等效電路寫出電壓方程(d軸變量用α表示,q軸變量用β表示):

式中:D表示電機的初級長度;Rs、Rr表示初級電阻、次級電阻;Lls、Llr、Lm表示初級漏感、次級漏感,勵磁電感;isα、irα、isβ、irβ分別表示 α 軸初級電流、α軸次級電流,β軸初級電流、β軸次級電流。
由式(3)可得磁鏈計算式:

式中:m表示電機質量;B表示粘滯摩擦系數。
若ωr為直線電機等效角速度,它與v的關系,轉矩Te與推力Fe的關系分別為:

式中:τ表示初級線組極距。
電磁推力方程式:

式中:p為電機極對數。根據式(4)、式(8)可得推力計算式:

由磁鏈方程可得電流計算式:

由式(3)推得磁鏈狀態方程:

由運動方程得等效角速度狀態方程:

把LIM的等效電路寫成狀態空間方程的形式,則:

LIM模型就是基于狀態方程建立的。
3 直接推力控制模型
LIM的直接推力控制即是把直接轉矩控制方法應用于LIM,其方法與旋轉感應電機一樣。如圖3所示,控制模型主要由PWM逆變器、直線感應電動機、磁鏈與推力計算模塊、磁鏈位置判斷、磁鏈調節器、推力調節器、電壓矢量選擇器組成。系統給定值包括:設定電機速度定子磁鏈以及負載推力Fload。電機輸出值包括:電機速度以及由速度計算所得的邊緣效應函數f(Q)、定子電流。

圖3 考慮邊緣效應影響下的直接推力控制框圖
三相PWM有8種不同的邏輯狀態,可以輸出8種不同的電壓矢量,包括6個非零電壓矢量和2個零電壓矢量。電壓矢量的選擇由三個量共同決定:推力滯環輸出eF、磁鏈滯環輸出量eψ以及磁鏈扇區位置sector。
磁鏈調節器采用兩電平滯環比較器,Hψ為磁鏈滯環寬度,表達式如下:

推力控制器采用三電平滯環比較器,HF為推力滯環寬度,表達式如下:

為了獲得快速準確的推力響應,需要按照如表1所示的規則選擇電壓矢量施加給LIM,便可將磁鏈和推力的波動范圍嚴格限制在其滯環寬度范圍內。
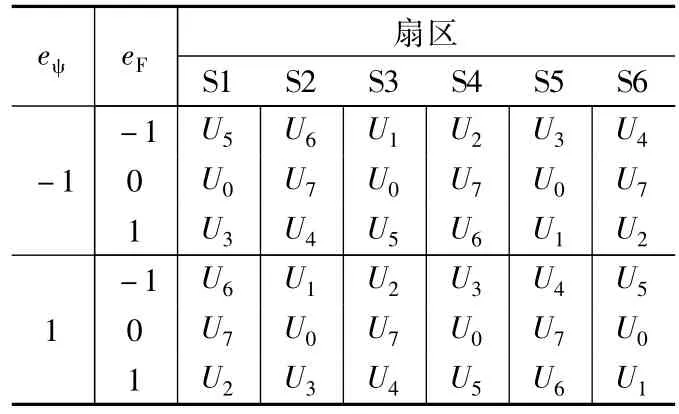
表1 電壓矢量控制選擇表
4 結果及分析
仿真用直線電動機參數如表2所示,給定定子磁鏈│ψs│=0.45 Wb,磁鏈滯環寬度設定為Hψ=0.005 Wb,推力滯環寬度設定為HF=0.01 N,電機推力限制值Fmax=2 385 N。

表2 直線電機參數表
(1)f(Q)與速度、互感與速度的關系
圖4a為f(Q)與電機速度v的關系,圖4b為電機勵磁電感L'm與速度v的關系。由圖4可知隨著速度的上升,邊緣效應的效果會增強,總勵磁電感值隨著電機速度的上升而下降。

圖4 f(Q)、勵磁電感與速度的關系
(2)空載時速度突變
以下為不考慮和考慮邊緣效應影響下的仿真結果對比。電機負載為空載;運行速度設置為:0~0.5s:2 m/s,0.5 ~1 s:8 m/s。
圖5為三相定子電流波形圖,圖6為圓形定子磁鏈軌跡,圖7為電機速度響應對比,圖8表示給定速度為8 m/s時的放大對比,圖9為電機推力響應對比。

如圖8、圖9所示,經過放大對比,當建立的電機控制模型不考慮邊緣效應影響時,速度和推力振蕩幅度明顯大于考慮邊緣效應影響時的,而且這種現象還會隨著電機速度v的上升而加劇,這是由于磁鏈和推力計算模型中沒有準確反映邊緣效應影響所造成的。而考慮了邊緣效應后,磁鏈和推力方程分別如式(4)和式(8)所示,LIM最終產生的速度和推力響應的振蕩幅度大為減小。
仿真結果表明,直接推力控制方法在LIM控制上取得了較為理想的效果,當速度指令值突變時,電機的動態響應速度快,穩態性能好。考慮動態縱向邊緣效應影響之后,LIM的運行性能得到有效改善。
5 結 語
本文將直接轉矩控制方法引入到LIM控制中,并將其特有的邊緣效應影響量化入等效電路中,實現了LIM的直接推力控制。仿真結果凸顯出直接推力控制方法在LIM控制上的簡單、快速有效性,同時說明了動態縱向邊緣效應對LIM運行時的速度和推力的振蕩幅度影響很大,不可忽視。在工程實際中,隨著運行環境的改變,LIM的各項參數通常是非線性、強耦合且時變的,必須建立更為正確有效的控制模型加以克服。
[1]Gieras J F.Linear Induction Drives[M].Oxford Science Publications,1994.
[2]Sung J H,Nam K H.A new approach to vector control for a linear induction motor considering end effects[J].Thirty-Fourth IAS Annual Meeting on Industry Application,1999(4):2284-2289.
[3]Susluoglu B,Karsli V M.Direct thrust controlled linear induction motor including end effect[C]//Power Electronics and Motion Control Conference.2008:850-854.
[4]Ozkop E,Akpinar A S,Okumus H I.Direct torque control for linear induction motor[C]//Power System Conference.2008:373-376.
[5]Itoh K,Kubota H.Thrust ripple reduction of linear induction motor with direct torque control[J].Proc.of the ICEMS,2005(1):655-658.
[6]葉云岳.直線電機原理與應用[M].北京:機械工業出版社,2000:40-48.
[7]Duncan J,Eng C.Linear induction motor-equivalent circuit model[J].IEE Proc.on Electric.Power Applications,1983,130(1):51-57.
[8]Kang G,Nam K.Field-oriented control scheme for linear induction motor with the end effect[J].IEE Proc.Electric Power Appl.,2005,152(6):1565-1572 .
[9]陳伯時,陳敏遜.交流調速系統[M].北京:機械工業出版社,2006:184~188.

