預防性維修計劃和生產調度的多目標優化

金玉蘭，蔣祖華

(1.上海工程技術大學 管理學院，上海200260;2.上海交通大學 機械與動力工程學院，上海200240)

預防性維修計劃和生產調度是生產企業所面臨的最常見和最重要的問題之一.預防性維修占據了本來用來進行生產活動的時間，同時，如果不進行預防性維修，又有可能在生產過程中發生突發故障，更大程度地影響生產進程.

為合理解決生產調度和預防性維修間的矛盾沖突，許多學者對預防性維修計劃和生產調度的聯合優化問題進行了研究［1-4］，主要集中在最小化加權總完工時間［1，3］、最小化加權總延遲時間［2］、最小化生產任務的最大完成時間［4］等時間目標的優化上，而對于維修的成本問題沒有涉及.有效的預防性維修計劃和生產調度計劃必須同時考慮到降低維修成本，提高生產效率.

本文對單設備預防性維修和生產調度的多目標優化問題進行了研究，并分別與單目標聯合優化的方法［1-3］和獨立優化的方法進行了對比.

1 預防性維修計劃和生產調度的多目標聯合優化模型

1.1 生產調度

假設一個生產系統中的一臺設備需要順序完成n個作業，pj為作業j的加工時間，dj為作業j的預定完成時間，wj為作業 j的重要性，j=1，2，…，n.生產調度計劃的目的是對n個作業進行合理的作業排序.令［1-2］

設 p［i］為作業序列中第 i個作業所用時間，d［i］為作業序列中第i個作業的預定完成，w［i］為作業序列中第i個作業的重要性，C［i］為作業序列中第i個作業的實際完成時間，T［i］為作業序列中第i個作業的延遲時間，i=1，2，…，n.若忽略設備的失效狀況，則［1-3］

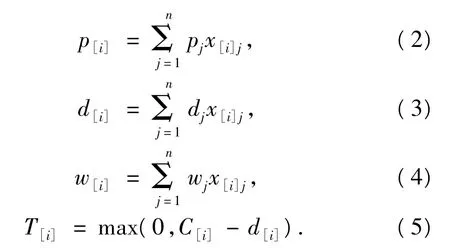
對生產調度計劃的制定，經常考慮到以下一些面向時間的目標，如:全部生產任務的最大完成時間(makespan)，加權總完工時間(total weighted completion times，TWC)，加權總延遲時間(total weighted tardiness，TWT)等.其中［3］:

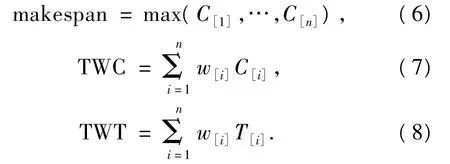
1.2 維修計劃

設備可靠性狀況、預防性維修策略、預防性維修處理時間、突發故障處理時間、突發故障次數等因素都會影響到生產任務中各個作業的最終完成時間［1］.因此，在生產調度時要同時考慮維修策略.同文獻［1-3］，將預防性維修計劃安排在作業序列中每個作業開始之前.假設預防性維修使設備的狀態修復到全新.生產過程中的突發故障用小修處理.設R0為加工整個作業序列前的設備初始可靠度，tp為預防性維修平均所需時間，tr為突發故障平均處理時間，cp為進行一次預防性維修的平均成本，cr為處理一次突發故障的平均成本.

設y［i］為作業序列中第 個作業加工前的預防性維修決策，則［1］

當生產設備的故障服從威布爾分布，形狀參數為β(β＞1)，尺寸參數為 η，則設備的可靠度R(t)和故障率λ(t)分別為

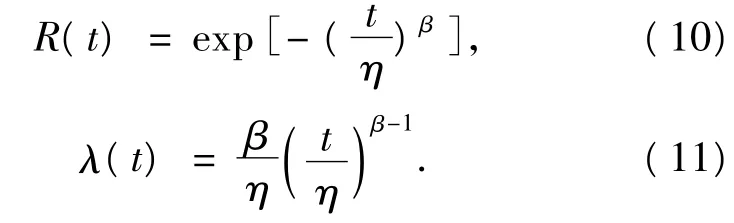
設從全新狀態始，設備運行時間τ內發生的故障次數為 N(τ)，則

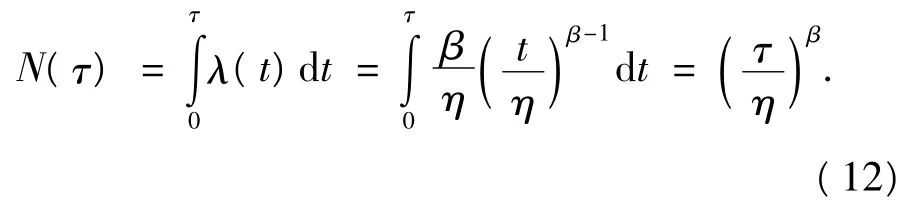
設as［i］為作業序列中進行第i個作業加工前的設備役齡，ae［i］為作業序列中完成第i個作業完成后的設備役齡，則［1］

根據式(10)，當加工整個作業序列前的設備初始可靠度為R0時有

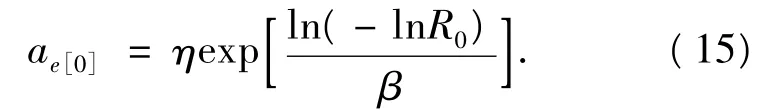
作業序列中第i個作業的完成時間C［i］為

設MC為完成整個作業序列所需的維修成本(maintenance cost)，則

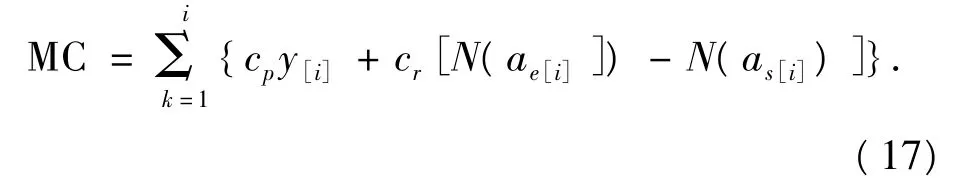
1.3 多目標聯合優化模型

為更好地節約維修成本和完成生產任務，設fk(k=1，2，3，4)為需要考慮的目標，則

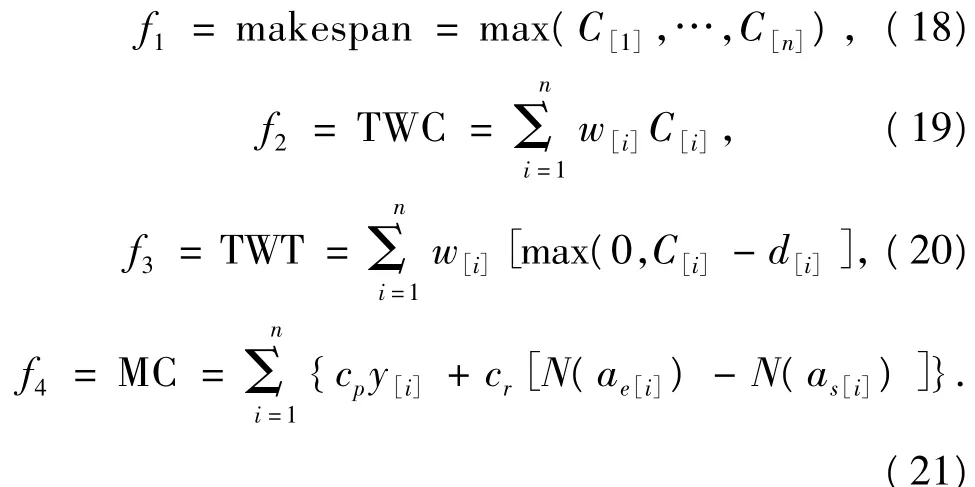
設 fopt為目標向量函數，fopt=(f1，f2，f3，f4)，則多目標優化模型為

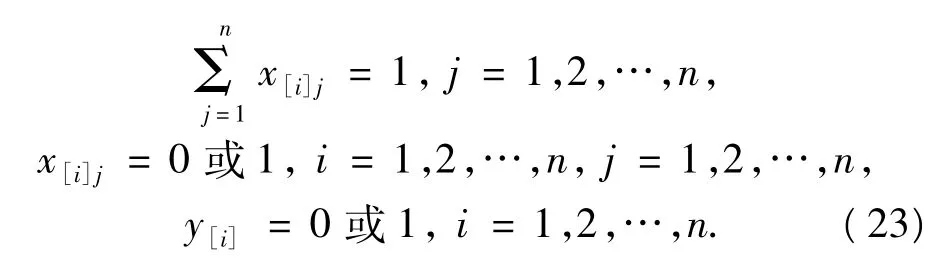
2 多目標遺傳算法

多目標優化問題常會存在一個Pareto最優集，集中的每個解都是多目標優化問題的一個非劣解，可為決策者作最終選擇所用.與大多數優化算法不同，遺傳算法可以提供一個種群的相似解，同時尋找到多個 Pareto優解［5］.

多目標遺傳算法是根據支配的概念來運作的［5］.如果說解x1支配x2，則必須滿足以下2個條件［5］:1)對于所有的目標x1非劣于x2;2)至少有一個目標x1優于x2.如果以上2個條件不滿足，則x1不支配x2.

2.1 編碼和初始種群

個體(染色體)采用實值編碼法.對于種群中的每個個體先隨機產生一個預防性維修序列，再產生一個隨機的作業序列.如個體{01104321}表示預防性維修序列為0-1-1-0，作業序列為4-3-2-1.隨機產生多目標遺傳算法的初始種群，種群的大小為Npop，Npop設定要適中，太小會使收斂速度變慢，太大則會增加搜索的難點，降低搜索效率.

2.2 精英策略

在多目標優化中，存在一組非被支配個體的集合 Eg(g=1，2，…，Gen，Gen 為算法的代數).在進行遺傳算法時，從Eg找出不同于Ei(i=1，2，…，g-1)中的非被支配個體，組成新集合Eg'.將Eg'中的個體保存在精英集中.從這個精英集中隨機選擇Nelite組個體作為遺傳算法中的精英［5］.

2.2.1 評價

對種群中的每個個體，按照1.1節和1.2節分別計算出各個目標函數.將種群中的個體按照是否支配其他個體進行分類，并將非被支配的個體保存在集合 Eg(g=1，2，…，Gen)中.

2.2.2 分類

下列過程可以找出種群中的非被支配個體［5］.

1)從i=1開始.

2)從 j=1，2，…，Npop，如果 i≠j，則根據支配的概念來判斷個體xi和個體xj之間的支配關系.

3)如果對于任意的j(i≠j)，xj都支配，xi則表示xi是被支配的.

4)如果種群中的所有個體都考慮了，轉步驟4);否則，轉步驟2).

5)除被支配的個體外，種群中的其他個體都是非被支配個體.

2.3 選擇

本文采用隨機加權法［5］將多目標轉化成單目標，從而計算個體的適應度.對目標 fk(k=1，2，3，4)線性正規化處理，設fmaxk和fmink分別為種群中目標fk的最大值和最小值，線性正規化后目標值vk(fk)為［6］

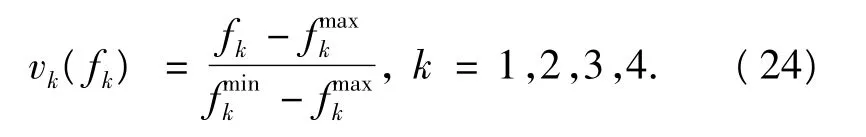
在選擇一組個體作為父代產生新個體時，用以下方法為各目標產生一個隨機權重:

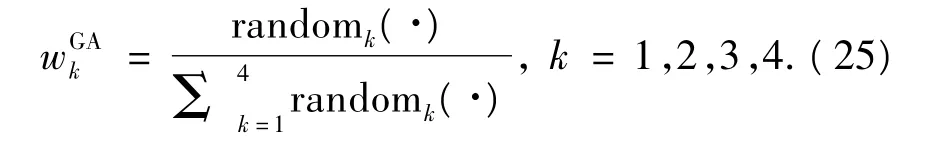
式中:randomk(·)為任意非負隨機數，且randomk(·)∈［0，1］.由式(24)、(25)得隨機加權適應度函數為

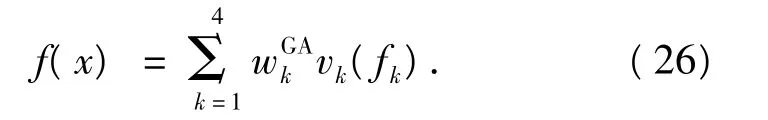
2.4 交叉

本文采用單點交叉，交叉點范圍為［1，2n-1］，n為作業序列中作業的個數，在交叉點之后的父個體的變量相互交換.當交叉點為［1，n］時，即交叉點在預防性維修序列中，則直接進行交換.當交叉點為［n+1，2n-1］時，即交叉點在作業序列中，則從交叉點之后父個體Parent1的作業序列為父個體Parent2中除去Parent1交叉點前作業后的作業序列［3］.

2.5 變異

本文采用單點變異，變異點的范圍為［1，2n］，n為作業序列中作業的個數.當變異點為［1，n］時，即變異點處于預防性維修序列中，將變異點值進行0和1之間的轉換.當變異點為［n+1，2n］時，即變異點處于作業序列中，將變異點處的作業轉移到作業序列的最后一個進行加工［3］.

2.6 多目標遺傳算法流程

1)根據2.1節產生初始種群Npop.

2)根據2.2節找出種群中的非支配個體集Eg和Eg'，并將Eg'保存在精英集中.判斷是否滿足優化準則，如果滿足，轉步驟7)，否則，轉步驟3).

3)從精英集中隨機選擇Nelite組個體作為父個體.其余(Npop-Nelite)組父個體從種群中選出.根據2.3節計算種群中各個體的隨機加權適應度函數，然后用輪盤賭的方法選出(Npop-Nelite)組父個體.

4)將Npop組父個體重新隨機組對.根據交叉概率pc和2.4節的交叉方法，生成一組新個體.

5)根據變異概率pm和2.5節的變異方法對新的個體進行變異操作.

6)對每組新個體根據2.2.1 節和2.2.2 節進行評價分類，并找出一個較優的個體作為新個體.如果沒有較優的個體，則隨機選擇一個作為新個體.Npop個新個體組成新的種群.轉步驟2).

7)根據2.2節的方法，從精英集中找出非被支配的個體作為Pareto最優集.

8)決策者根據偏好從Pareto最優集中選出滿意解.

3 算例分析

3.1 算例及結果

假設設備的初始可靠度R0=0.8;故障服從威布爾分布，形狀參數β=1.8，尺寸參數η=100;預防性維修處理時間tp=5，小修處理時間tr=15;預防性維修成本cp=500，小修的成本cr=300.有4個作業需要進行加工，其參數見表1.

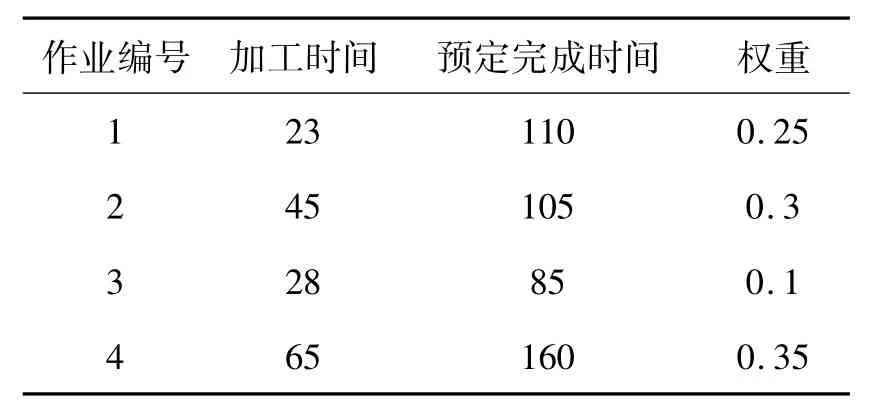
表1 生產調度參數示例Table 1 Factors of production scheduling in the example

將以上參數代入優化模型，在Visual Basic 6.0中編程實現多目標遺傳算法.當遺傳代數Gen=30，種群大小 Npop=30，交叉概率 pc=0.8，變異概率pm=0.7，Nelite=3 時，所得優化結果見表2.

一般情況下預防性維修次數越多，則突發故障的產生次數越少.由表2可知，對于特定的生產要求(如表1所示)由于cp＞cr所以維修成本(MC)還是隨維修次數的增多而升高.由表2可知，加權總完工時間(TWC)和加權總延遲時間(TWT)則同時受作業序列和預防性維修序列的影響.當預防性維修次數相同時，對于相同的作業序列，TWC和TWT隨預防性維修序列的變化而小幅變化;對于相同的預防性維修序列，TWC和TWT隨作業序列的變化而發生較大幅度的變化.makespan主要受預防性維修序列的影響，作業序列對makespan的相對較小.

由表2可知，多目標聯合預防性維修計劃和生產調度計劃所得的 makespan的最小值為190.2，TWC 的最小值為105.1，TWT 的最小值為 10.7，MC的最小值為1 020.0.但沒有一組預防性維修計劃和生產調度計劃使得4個目標同時最優，因此決策者可根據偏好信息決策出的滿意解.

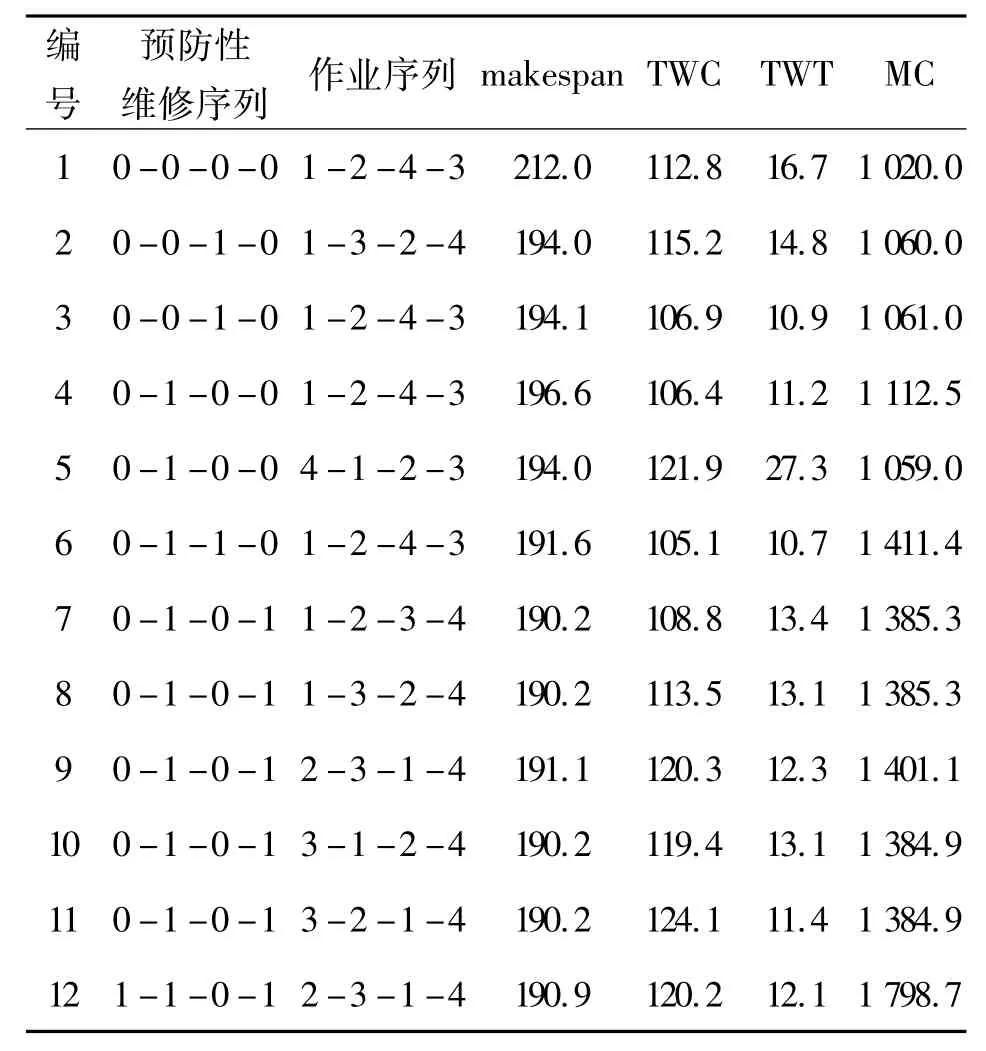
表2 多目標遺傳算法的優化結果Table 2 Multi-objective genetic algorithms simulation results

3.2 方法對比

將本文所提的預防性維修計劃和生產調度多目標聯合優化方法分別跟單目標聯合優化方法和獨立優化方法進行比較.

1)單目標聯合優化方法.若應用文獻［1-2］的方法，將本文所示范例進行預防性維修計劃和生產調度計劃的單目標聯合優化.當優化目標分別為makespan和MC時，經枚舉所得的優化計劃結果不唯一，makespan和 MC的最小值分別為190.2和1 020.0.當優化目標分別為TWC和TWT，所得最優結果相同且唯一，預防性維修序列為0-1-1-0而生產作業序列為1-2-4-3，TWC和TWT分別為最小值105.1和10.7，此時makespan和MC分別為191.6 和 1 411.4.

對比表2可知，本文的多目標聯合優化的Pareto最優集中包含了預防性維修計劃和生產調度計劃的單目標聯合優化的優化結果.當決策者要考慮多個優化目標時，單目標聯合優化的效率顯然較差.

2)獨立優化方法.將預防性維修計劃和生產調度計劃分別進行獨立優化.預防性維修計劃采用使設備可用度達到最優的基于壽命的維修策略［1］，而生產調度計劃采用多目標(makespan，TWC，TWT)優化.由文獻［1］可知，當 β =1.8，η =100，tp=5，tr=15時，設備從全新狀態開始，經過61.5單位時間后進行預防性維修，R(61.5)=0.66，即當設備可靠度降到0.66時，進行預防性維修.對生產調度計劃單獨進行多目標優化的結果為:1-2-3-4、1-2-4-3、1-3-2-4.將2種優化計劃組合起來，計算makespan、TWC、TWT和 MC 見表3.由表 3 可見，最優結果為預防性維修開始時間序列為18-79.5-141且作業序列為1-2-4-3.

表3 預防性維修計劃和生產調度計劃的獨立優化結果Table 3 Calculated results of separately optimizing PM planning and production scheduling in the example

對比表2可知，本文的多目標聯合優化的Pareto最優集包含了預防性維修計劃和生產調度計劃獨立優化的結果.對于表3中的任意計劃，都能從本文的多目標聯合優化的Pareto最優集中找出比其更優的計劃.因此，本文的聯合方法要優于獨立優化方法.

4 結束語

本文提出了單設備預防性維修計劃和生產調度的多目標優化模型.通過實例可知，一般情況下預防性維修次數越多，則突發故障的產生次數越少.在預防性維修成本高于小修成本的情況下，MC主要隨預防性維修次數的增多而升高.TWC和TWT則同時受作業序列和預防性維修序列的影響.Makespan主要受預防性維修序列的影響.

本文未對決策者如何從多目標聯合優化的Pareto最優集中選出滿意解作闡述，當最優集規模較大時，這一問題值得探討.對于多臺設備、多種預防性維修方式或flowshop生產計劃問題等，還需要對預防性維修計劃和生產調度的多目標優化方法進行更深入的研究.

［1］CASSADY C R，KUTANOGLU E.Integrating preventive maintenance planning and production scheduling for a single machine［J］.IEEE Transactions on Reliability，2005，54(2):304-309.

［2］應保勝，但斌斌，張華.生產計劃和預防性維修計劃的統籌優化模型［J］.機械工程學報，2005，41(3):226-228.YING Baosheng，DAN Binbin，ZHANG Hua.Optimization model by integrating preventive maintenance planning and production scheduling［J］.Chinese Journal of Mechanical Engineering，2005，41(3):226-228.

［3］SORTRAKUL N，NACHTMANN H L，CASSADY C R.Genetic algorithms for integrated preventive maintenance planning and production scheduling for a single machine［J］.Computers in Industry，2005，56(2):161-168.

［4］RUIZ R，CARLOS G J，MAROTO C.Considering scheduling and preventive maintenance in the flowshop sequencing problem［J］.Computers＆ Operations Research，2007，34(11):3314-3330.

［5］OSMAN M S，ABO-SINNA M A，MOUSA A A.An effective genetic algorithm approach to multiobjective routing problems(MORPs) ［J］.Applied Mathematics and Computation，2005，163(2):769-781.

［6］王小平，曹立明.遺傳算法——理論、應用與軟件實現［M］.西安:西安交通大學出版社，2002:115-122.WANG Xiaoping，CAO Liming.GA—theory，application and software［M］.Xi＇an:Xi＇An Jiao Tong University Press，2002:115-122.