基于Hypermesh/OptiStruct的發動機支架結構拓撲優化設計

唐 濤

（鎮江高等專科學校，鎮江 212003）

0 引言

為提高發動機支架加工的經濟性和降低生產成本，發動機支架結構的輕量化設計與研究逐漸被越來越多的發動機制造企業所重視。目前發動機支架的輕量化工作主要是從材料和結構兩方面著手。通過尋找新型功能材料替代傳統的鋼和鑄鐵是減重的有效方式之一。結構方面，現代發動機支架無論是整體造型還是各功能部件的布置，都與傳統發動機支架發生了比較大的變化。近年來興起的結構優化設計是根據算法合理分配優化對象（比如尺寸等設計參數、形狀、材料）以保證發動機支架整體的剛度等特性，從而讓支架結構設計擺脫了對應驗的盲目依賴。結構優化設計主要分尺寸優化、形狀優化、形貌優化和拓撲優化。拓撲優化相對于尺寸優化和形狀優化，具有更多的設計自由度，能夠獲得更大的設計空間，是結構優化最具發展前景的一方面。

1 拓撲優化技術

結構拓撲優化是近20年來從結構優化研究中派生出來的一個新興的分支。拓撲優化是根據既定的結構類型、形式、工況、材料和規范所規定的各種約束條件（如強度、剛度、頻率等），提出優化的數學模型（包括目標函數、約束條件和設計變量），其模式是根據優化設計的理論和方法求解優化模型，最后達到材料的合理分配，使結構滿足設計要求[1]。這使得人們在解決工程問題時，可以從無數設計方案中找到最優或者盡可能完善的設計方案，從而大大提高工程設計效率。目前拓撲優化技術已成為結構優化設計的重要方法，廣泛應用于航空、造船、工程機械、汽車機械、機床制造業等行業，并取得大量研究成果[2]。

1.1 拓撲優化原理和優化方法

拓撲優化是結構優化的一種，其研究領域主要分為連續體拓撲優化和離散結構拓撲優化，不論哪個領域，都有依賴于有限元方法。結構拓撲優化是在一定的外力和作用下，尋求具有最佳傳力路徑的結構布置形式。對于連續體的結構的拓撲優化設計問題，基本方法是將設計區域劃分為有限單元（比如殼單元或者體單元），并依據一定的算法刪除部分單元區域，形成帶孔的連續體，從而實現連續體的拓撲優化，其本質上是一種0-1離散變量的組合優化問題。離散結構拓撲優化是在設計空間內建立一個由有限個梁單元組成的基結構，把離散變量的優化問題松弛為一個連續變量的優化問題，將基于連續變量的導數優化算法應用于優化中，也就是用連續設計變量的優化模型替代原離散的設計模型，從而實現拓撲優化。目前連續體拓撲優化方法主要由均勻化方法、變密度法、漸進結構優化法（ESO）以及水平集中法等。離散結構拓撲優化主要是在基結構方法基礎上采用不同的優化策略（算法）進行求解，比如基于遺傳算法的拓撲優化等。目前，連續體拓撲優化的研究已經較為成熟，其中變密度法已經被應用到商用優化軟件中，其中最著名的是美國Altair公司Hyperworks系列軟件中的OptiStruct優化模塊和德國Fe-design公司的Tosca等。前者能夠采用Hypermesh作為前處理器，在各大行業內應用最多。

1.2 變密度算法的原理和數學模型

變密度算法是引入一種假想的密度可變材料，將連續體離散為有限元模型后，將每個單元內的密度指定為相同，并以每個單元的密度為設計變量。當每個單元的相對密度Xe=1時，則表示該單元為有材料，保留或增加該單元（實體）；當Xe=0時，表示該單元沒有材料，單元應該刪除（孔洞）。拓撲優化時，應盡量使材料的相對密度為0或者1分布在設計區域。

以結構的柔順度（變形能）最小為目標，考慮材料質量約束（或體積約束）和結構的平衡條件，則變密度法拓撲優化數學模型為：

求X=(X1, X2, X3…XN)T

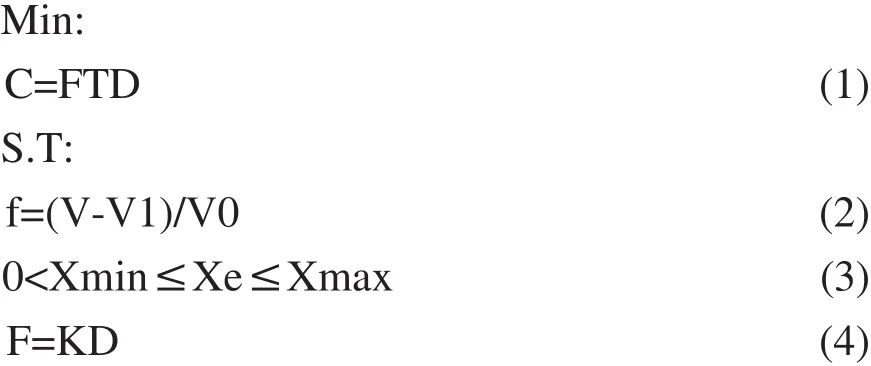
式中,C為結構的柔順度；F為載荷矢量；K為剛度矩陣；D位移矢量；V為結構充滿材料的體積；V0為結構設計域的體積；V1為單元密度小于Xmin的材料的體積；f為剩余材料百分比；Xmin為單元相對密度的下限；Xmax為單元相對密度的上限[3]。

2 實例應用

2.1 發動機支架結構

2.1.1 建立發動機支架的CAD/CAE模型

通過三維CAD建模軟件SolidWorks建立起發動機及其支架的幾何模型。由圖1可以看出，該型號發動機通過上下兩根連接螺栓與發動機支架相連。發動機本身質量是108Kg，發動機的重力通過兩根連接螺栓加載在支架上；同時，由于發動機轉動時會產生振動，通過連接螺栓會帶動支架做振動。因此，在實際的CAE分析中，可以將發動機簡化為一個質點，賦予之108Kg的質量；同時，該質點與螺栓連接的方式是RB3，即該質點與支架螺栓孔之間不是剛性連接而是可以做相互運動，如圖3所示。

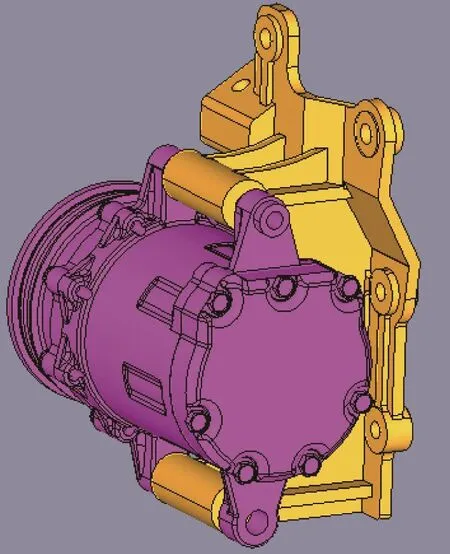
圖1 發動機及支架的三維模型

2.1.2 發動機支架結構

該發動機的結構通過傳統的經驗、類比設計方法得出，主要由1塊底板和2塊縱向肋板構成如圖2所示。支架上有2個用于與發動機相連接的螺栓孔，5個與支架底座連接的螺栓孔。這5個螺栓孔在與支架底座相連接時，螺栓孔可視為剛性結構，在CAE模型中用RB2連接方式表示如圖3所示。盡管支架的結構已經較為簡化，但是支架底板仍顯得笨重，還有一定的輕量化的空間。

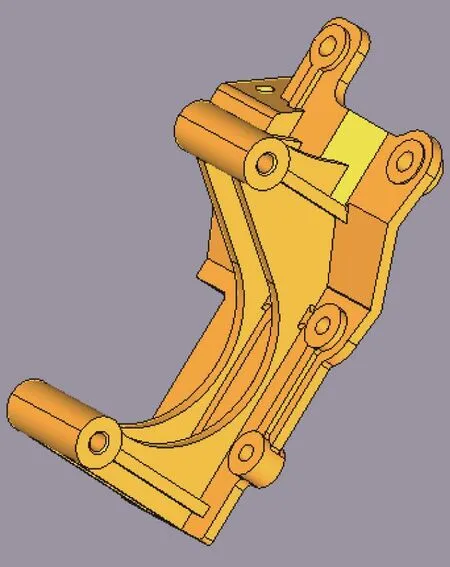
圖2 支架的三維模型

2.2 發動機支架的優化

2.2.1 發動機支架有限元模型的靜態特性和動態特性分析

考慮到優化對象是支架，只需將三維支架的CAD模型導入到分析軟件HyperMesh中，得到其有限元模型。通過HyperWorks自帶的HyperMesh軟件進行有限元單元劃分。HyperMesh具備強大的單元劃分和重構功能，利用該軟件對發動機支架進行網格劃分，并檢查網格質量，務必使單元網格質量都符合計算要求。在劃分支架體單元時，為保證后續有限元分析和拓撲計算的精確性，取支架的單元網格是二維單元網格。支架的結構是個連續體，質量和彈性連續分布，應具有無窮多個自由度，即具有無窮多階模態。發動機主軸最高轉速達到3500r/min，因此外界的激振力的頻率應該遠遠低于發動機運行時產生的激勵力頻率，沒有共振的可能，對發動機運行影響不大。所以只需要研究如何提高支架的低階模態的固有頻率，以便能夠有效地降低因發動機啟動時共振的可能性。發動機支架的前三階模態能夠明顯表現出支架的動態特性。取支架的材料是HT200，取彈性模量E=2.1e5 MPa；泊松比= 0.3；密度 7.9e-9ton/mm進行計算。

2.2.2 發動機支架CAE模型的拓撲優化分析

由于發動機支架是通過5個固定螺栓孔與底座相連，因此，需要給這5個螺栓孔賦予全約束。發動機的重力可視為支架的外載荷，其與支架的連接方式通過RB3明確下來。在確定發動機支架的載荷和邊界條件后，拓撲優化分析還需要明確優化參數。首先定義發動機支架的拓撲優化變量及優化變量的取值空間。圖3中黃色區域是發動機支架的螺栓孔位置，不能參與拓撲優化，需要排除在優化變量空間之外；相應的藍色區域就是拓撲優化變量的取值域。

設置了優化變量后，下一步要完成的是明確拓撲優化的目標和約束條件。此處，以提高發動機支架的剛度為目標，以一階固有頻率不低于原值為約束條件進行設置。OptiStruct優化模塊用柔度來體現剛度。柔度是剛度的倒數，柔度越小則剛度俞大。優化的目標和約束都是建立在響應的基礎上。顯然，剛度目標的響應是柔度，目標值取最小（min）；優化約束的響應是一階固有頻率，取不低于原值。圖4為是經過9次的優化迭代后計算出來的支架的變形密度云圖。

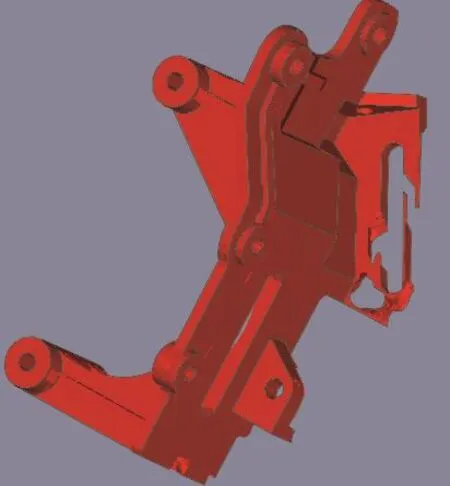
圖4 經過9次迭代后支架拓撲優化效果圖

2.2.3 發動機支架改進及與優化前的比較

拓撲優化的結果大都是不規則的空間結構，需要對拓撲優化結果進行抽象和簡化。新的支架結構改進工作是建立在拓撲優化密度云圖的基礎上。根據拓撲優化密度云圖，在支架底板上開鑿出1個腰形孔和1個方孔。改進結構后發動機支架的三維立體圖如圖5所示。

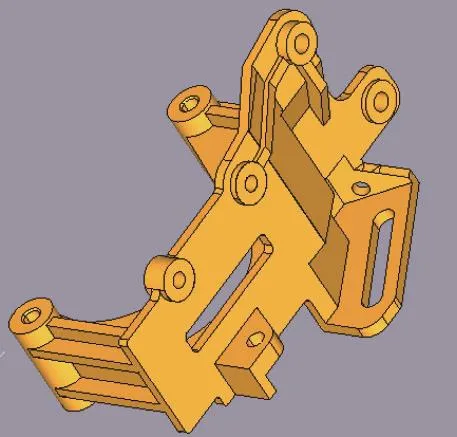
圖5 根據拓撲優化結果改進后的支架結構

將此發動機支架重新進行靜態特性和動態特性分析分析，并與原支架進行比較，得出結果見表1。

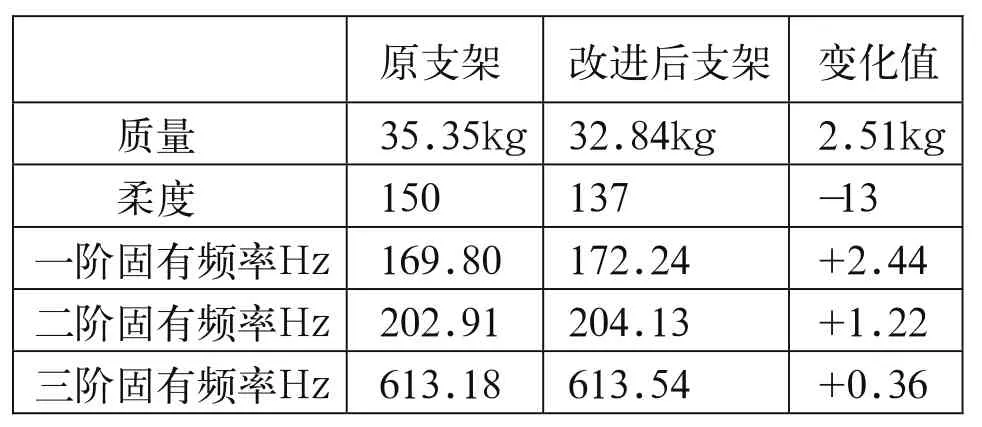
表1 支架拓撲優化前后性能指標的對比

改進后的發動機支架的柔度稍微有所降低，即剛度有所提高；前三階固有頻率都有所提高，同時質量降低了2.51Kg，可以說基本上達到了優化的目標。同時，新支架的結構改變之處，加工工藝非常容易達到，不會給支架的改進工作帶來非常大的困難。

3 結論

綜上所述，建立在限元分析基礎是的拓撲優化技術為結構的優化改進工作提供了方向性的指導。發動機支架輕量化設計技術與應用將會大大降低機床材料的消耗，為生產“節能減排，綠色環保”發動機及相關產品探索了一條新路。隨著拓撲結構優化理論的進一步成熟，發動機支架的輕量化工作將會對我國汽車及相關產業的發展產生越來越大的積極作用。

[1] 左再思,黃錦能.拓撲學[M].武漢:武漢大學出版社,1992.

[2] 儲乃雄.機床動態設計原理與應用[M].上海:同濟大學出版社,1987:1-32.

[3] 楊樹凱,朱啟昕.基于有限元技術的汽車支架拓撲優化設計研究[J].汽車技術,2006:3.

[4] 郗沭平,高萬盛,劉寶新.汽車電控技術簡明教程[M].北京:北京理工大學出版社,1999:172-182.

[5] 王世如,王金金,馮有前,等.計算方法[M].西安:西安電子科技大學出版社,2004.

[6] 段克峰,二次函數在閉區間上的最值估計[J].中學數學,2008.223(11):24-25.