數控裁板鋸的下鋸優化研究

劉玉娟，徐凱宏，馬 巖，董本志，楊春梅

（東北林業大學 林業與木工機械工程技術中心，哈爾濱 150040）

0 引言

隨著人民生活水平不斷提高，人們對居住環境、生活和工作空間舒適程度的重視也在不斷加強，中高檔家居和辦公家具產品的需求量呈上升的勢頭。在國內市場上，我國家具制造業很好，需求額以每年10%～15%的速度遞增，人造板的需求總量也在不斷迅速增加。因此能否找出切割板材下鋸優化的方法，以滿足板材需求現狀，并盡可減少板材的浪費，顯得尤為重要。家具生產所需的人造板的形狀主要是矩形的，這就將下鋸優化的問題轉化成矩形排樣優化問題。所謂矩形排樣優化問題即是一個多目標優化問題，既要考慮板材的利用率，又要考慮加工時的下料。本文研究的數控裁板鋸是用來加工應用在家具生產加工所需的矩形零件的。它符合“一刀切”的加工工藝要求，這就要求采用一種方法來進行下鋸優化，即余料最優處理。

1 矩形件的排樣優化問題的提出

為了在市場競爭中立于不敗之地并創造更多的效益，企業將會不斷提高其生產效率。而一個好的排樣方案可以節省原材料。但如果單純考慮材料的利用率，在矩形件種類較多時會加大排樣的復雜度，這樣不但會影響生產過程中的下料的效率，而且會延長生產加工的時間。因此需要找到一個既考慮到材料利用率與下料效率，又能考慮到生產效率與“一刀切”的工藝要求的排樣算法。

矩形件的排樣問題是指在給定的矩形板材上將一些需要排樣的矩形件以最優的方式排放在其上，以使材料的利用率達到最高，從而達到節省材料的目的[1]。好的排樣方式可以在經濟上制造非常可觀的效益。從理論角度來看，矩形排樣優化問題具有最高計算復雜性的問題，即NP完全問題[2]。對于NP完全問題至今還未找到多項式算法求解，因此只能采用近似的算法求解。對于矩形件的排樣優化，任何算法都難以保證得到的總是最優解，國內外學者已提出了一系列的近似算法[3～6]，這些算法也達到了所期望的材料利用率。本文將根據數控裁板鋸和板材的自身特殊點，研究一種新矩形件優化排樣的算法。并對二維矩形件的下鋸優化的算法開發了可用于該設備的計算機輔助排樣軟件。

2 下鋸優化的約束條件及數學模型的建立

2.1 下鋸優化的約束條件[7]

1）各矩形件之間相互不重疊；

2）矩形件的排放不能有超出板材的區域；

3）對于已經排放好的矩形件不能再移動其位置，即符合定序原則；

4）符合最右最低原則，即第一個排放的矩形件應放在板材的右下角，其余的矩形件則盡可能的排放在剩余區域的最右最低的位置；

5）滿足“一刀切”的工藝要求。

“一刀切”下料又稱直線切割，所謂“一刀切”是指保持切割線平行于板材的一個邊，每一次切割都必須由板材的一端沿直線至另一端，對裁開的板材繼續采用這個方法切割，一直到滿足需求為止。圖1（a）和（b）分別是一刀切模式與非一刀切模式的示意圖。

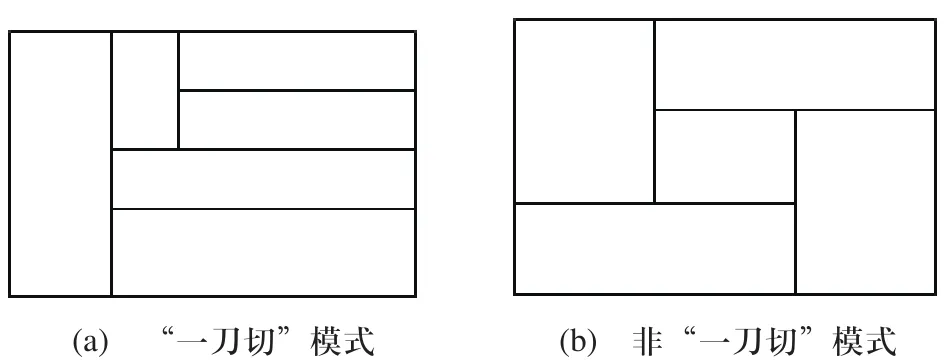
圖1 “一刀切”與非“一刀切”模式示意圖

2.2 數學模型的建立

根據裁板鋸的切割及運動的方向，板材排樣的排樣次序是自右向左、自下向上的。設板材的長和寬分別為L、W，有n（一般n≤10）種矩形件，其長、寬、數量分別用 li、wi、ni（1≤ i≤ n）表示。一般wi≤li≤W≤L。可得所有要排的矩形件的個數設總共用了N長板材，目的是在互不重疊的條件下把矩形件盡可能多的排列在板材上，并提高板材的利用率，即盡量減少使用的板材數量，并使余料盡可能多。

排在板材上的第一種矩形件有n種選擇。假設選擇了第i種零件，則一排最多可以放L/li個矩形件，最多可以排W/wi行。設在排樣中每行排了x個零件，共排了y行，即有1≤x≤min [L/li]；1 ≤ y≤ min [W/wi][2]。

2.3 下鋸優化算法的基本描述及下鋸優化算法及流程

所謂最低水平線法就是不斷更新水平線集的一種排樣算法，其主要思想就是選擇水平線集合中高度最低的那條，將要排放的零件排放在最低水平線上并更新水平線集，如果排不下則搜索與最低水平線左右兩邊相鄰的水平線，選擇高度較低的一條，將最低水平線提升至該高度，判斷更新后的最低水平線能否排入該零件，若依然排不下則繼續執行提升水平線的操作，直至能排入為止[8]。

本文采用的是基于最低水平線的選擇算法，是基于最低水平線的一種改進算法。其具體步驟如下：

1）首先將矩形件按寬度從大到小的順序進行排列，并同時列舉出矩形件的邊長數據；

2）設置初始最低水平線段為板材最下面的邊和設置初始最大高度Hmax為0[9]；

3）排入待排序列的第一個待排板材的矩形件，并更新最低水平線段與最大高度Hmax，如果最低水平線有數段則選擇從最右邊的那段開始排；

4） 每當要再排入一個矩形件時，測試其寬度是否既小于或等于最低水平線段的寬度又小于或等于最低水平線與最大高度Hmax之間的距離；

（1）若都小于或等于，則判斷其長度是否小于或等于最低水平線的寬度；

①若小于或等于則將該矩形件在此位置橫放，并其從待排有序矩形件集中刪除，同時更新最低水平線段和最大高度Hmax；

②否則判斷其長度是否小于或等于最低水平線與最大高度Hmax之間的距離；若小于或等于則將該矩形件在此位置豎放，并其從待排有序矩形件集中刪除，同時更新最低水平線段和最大高度Hmax。否則轉至（2）；

（2）依次從待排有序矩形件集中查找寬度小于該最低水平線段寬度的矩形件，如果找到則轉至（1）。如果沒有找到則更新最低水平線，直至最低水平線與最大高度Hmax重合，轉至3）；

5）最低水平線的最大高度是否達到板材邊界，若達到則更換一張新板材并轉至2），否則轉至6）；

6）重復4）到5）的過程，直至排入所有矩形件，并求出此時的最大高度即為所需板材的高度。

下鋸優化算法流程圖如圖2所示。

3 計算實例及分析

本文的目的是使最大高度Hmax以下的部分沒有填充的面積最小，并且Hmax以上的部分面積盡可能的大，以此提高整體的利用率。下面以下列規格的矩形件為例，應用上述優化算法進行排樣。表1為10種需要切割的矩形件。設原板材的尺寸大小為2440×1220mm，其中表是按矩形件寬度的遞減順序排列的。

應用上述方法對表1進行排樣，首先，先把同種的矩形件拼成一個大矩形，然后再寬度遞減的順序排列新的矩形件。其排樣結果如圖3和圖4所示。

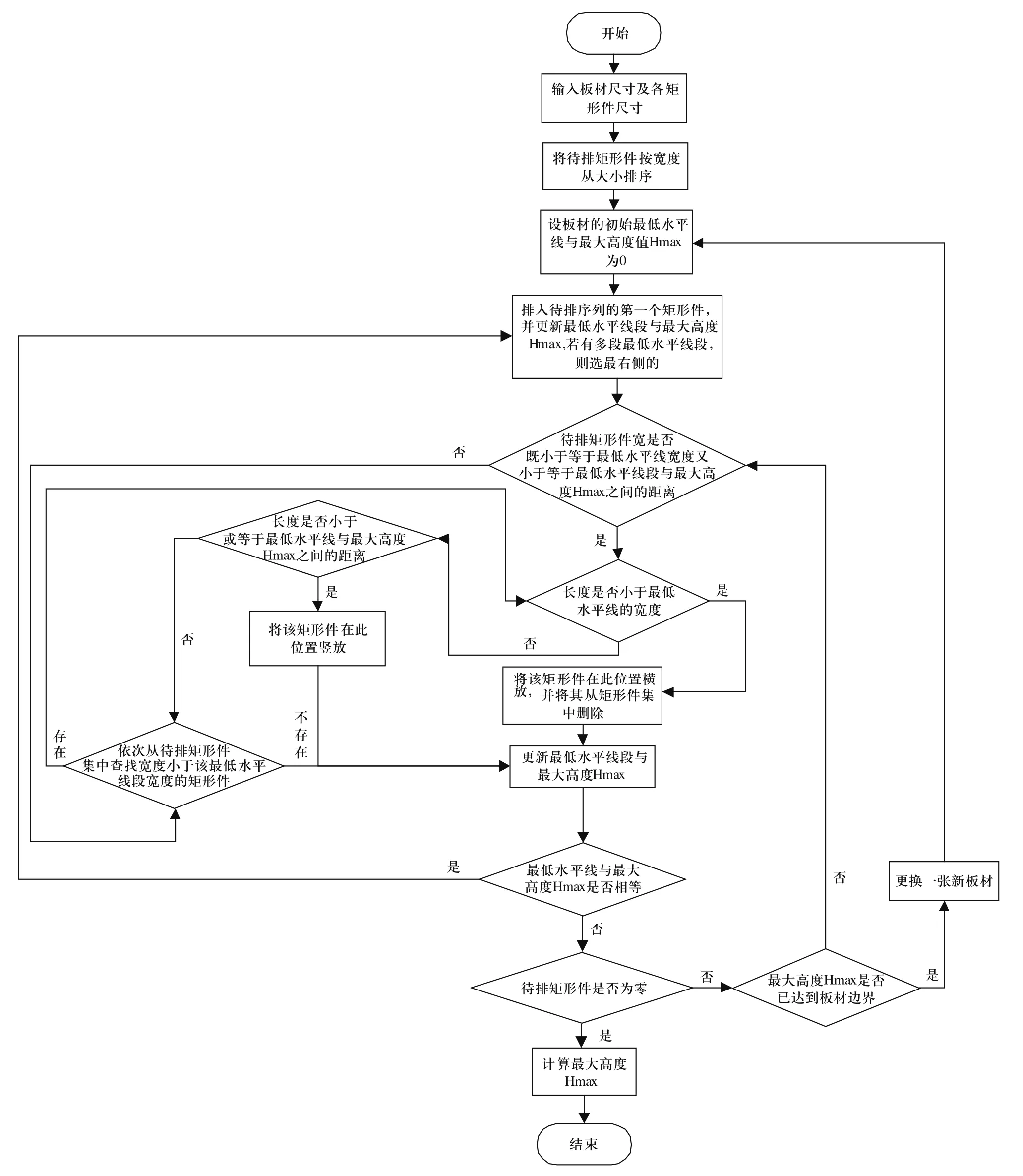
圖2 下鋸優化的流程圖

第三塊板材剩下的板材下次排樣的時候可以繼續使用。實踐證明，排樣的矩形件的種類、個數及板材的尺寸都會對板材的利用率有很大的影響。矩形件的種類越多，板材的尺寸越多利用率就越大。加工的時候要注意批量生產可以大大的提高板材的利用率。

4 結論

通過對實例的分析表明本研究的矩形件排樣方法能夠良好的解決數控裁板鋸的下鋸問題，它符合多種尺寸的板材的排樣，并且既可以達到優化的效果又可以使可用余料面積相對較大。且操作比較簡單，效果明顯并適合解決較大規模的排樣問題。同時，還可以應用到比較相似的切割問題上，具有較強的靈活性與應用性。

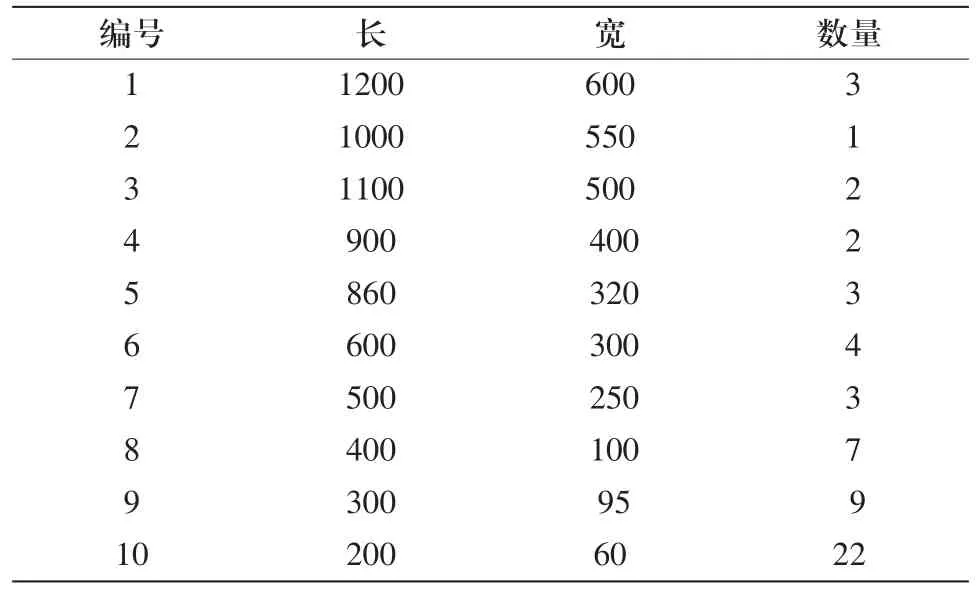
表1 10種待排矩形件的尺寸列表（單位：mm）

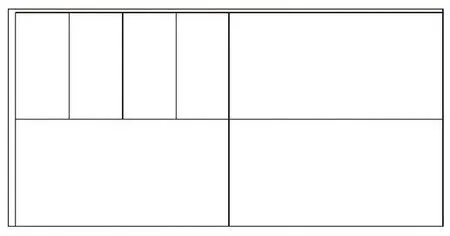
圖3 第一塊板材的利用率：98.32%，最大高度Hmax為1200mm

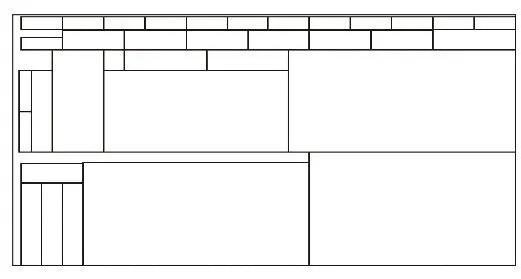
圖4 第二塊板材的利用率：93.88%，最大高度Hmax為1210mm

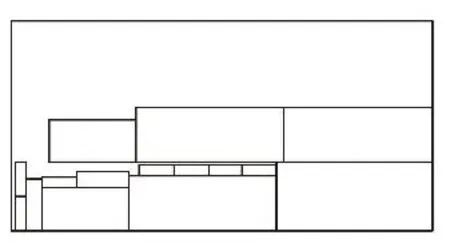
圖5 第三塊板材的利用率：59.96%，最大高度Hmax為720mm

[1] 楊傳華, 吳錦文, 李亞芹, 郭士清. 定序列矩形件優化排樣的二維搜索算法[J]. 佳木斯大學學報(自然科學),2010, 28(3): 354-356.

[2] 李勇, 曹炬, 梅晚霞, 方仍存. 矩形件排樣優化的十字線法[J]. 鍛壓裝備與制造技術, 2004, (6): 98-100.

[3] 曹炬, 周濟, 余俊. 矩形件排樣優化的背包算法[J]. 武漢:中國機械工程, 1994, 5(2).

[4] 方仍存, 曹炬, 陳學松. 矩形件排樣優化的一種近似算法[J]. 鍛造技術, 2005(6): 19-20.

[5] Yanasee HH. Two-dimensional cutting stock with multiple stock sizes. The Journal of Operational Research Society.1991, 42 (8): 673-683.

[6] Chaung F A. Two-Phase Heuristic for the Two-Dimensional Cutting Stock Problems. The Journal of Operational Research Society, 1991, 42 (1): 39-47.

[7] 呂俊豐, 馬巖, 喻虎德. 人造板一刀切數控下鋸優化的編程模型研究[J]. 木材加工機械, 2009(5): 12-15.

[8] 王竹婷, 劉林, 程浩, 劉心報. 改進的最低水平線搜索算法求解矩形排樣問題[J]. 工程設計學報, 2009, 16(2): 98-102.

[9] 朱冠華. 矩形件排樣中基于最低水平線的改進算法[J].茂名學院學報, 2006, 16(1): 28-32.