自然環境下路面裂縫的識別
馬常霞 , 趙春霞, 狄 峰, 李旻先
(1. 南京理工大學計算機科學與技術學院,江蘇 南京 210094;2. 淮海工學院計算機工程學院,江蘇 連云港 222005)
道路交通在國民經濟和人民生活中占有重要的地位。隨著道路建成后的不斷使用,對其合理有效的保養和維護就成為主要問題。定期調查道路路面狀況,并做出相應的維護措施,以便在路面病害出現的早期就發現它、修繕它是路面維護的基本思路。傳統的基于人工視覺檢測病害的方法花費大、效率不高、影響交通、檢測結果不可靠存在因人而異的現象,因此不能適應道路發展的需要。迫切需要提出一種快速有效的路面病害檢測方法。
初期使用攝像機的路面裂縫識別系統是一種基于人工或計算機輔助的人工評價,即半自動化的檢測。由工作人員檢查存儲在計算機硬盤上的路面圖像,在圖像上標注出裂縫,再由計算機進行統計。后來的計算機輔助半自動裂縫識別系統通過一些路面圖像處理算法進行裂縫識別,提高了系統自動化水平。這些算法的基本目的是從一個二值圖像中抽取裂縫特征。二值圖像一般通過確定一個最佳閾值來得到,大于閾值的像素被認為是背景,設為白色像素;小于閾值的認為是裂縫,設為黑色像素,從而提取出裂縫。但是,由于路面圖像中存在許多隨機的噪聲信息,確定一個適用于所有路面圖像的閾值很困難,這樣的處理并不能很準確地識別裂縫。所以,工作人員還必須仔細檢查處理過的圖像,人工糾正漏檢和誤檢。
近年來,基于圖像的路面病害自動檢測已成為各國競相研究的課題。它利用高速度、高精度的攝像機快速的拍攝路面圖像,利用計算機快速處理,得到病害信息。目前主要的裂縫檢測算法主要有人工種群算法[1]、多級擬合機制的檢測方法[2]、基于三維地形模型的路面裂縫自動檢測算法[3]、基于高速公路裂紋局部線性特征內容的脊波變換域算法研究[4]。這些算法都在一定程度上對常規裂縫檢測算法有所改進,但均存在難以克服大量隨機分布的噪聲的影響,對一些輕微裂縫及網狀裂縫仍然不能取得預期的效果,而且運算量過大,不利于對大量的路面圖像的處理。
本文提出一種基于分數階微分演算和圖像形態學的路面圖像增強及檢測病害的方法。首先由于分數階微分運算在加強信號高中頻成分的同時,也對信號的甚低頻成分進行了非線性保留,所以通過分數階微分運算增強路面圖像,可以使處于平滑區域的弱信號裂縫病害信息得以加強。然后在此基礎上通過一組中值濾波過濾店大量的隨機噪聲,利用形態學算子檢測出裂縫邊緣,并細化提取出最終的裂縫骨架。
1 分數階微分運算應用于圖像處理
長期以來,分數階微分主要被數學家作為一種純數學理論來研究。由于沒有得到實際應用背景的促進,發展相對比較緩慢。在近幾十年里,分數階微分理論才在化學、電磁學、控制學、材料科學和力學中引起廣泛關注并做了一些嘗試性的應用。將分數階微分應用于圖像信號處理,在國內外還是一個新的研究領域。
1.1 分數階微分的定義
常用的分數階微分定義有三種,即G-L型分數階微分,R-L型分數階微分,Caputo型微分。
G-L定義將連續函數的整數階微分的階數通過對原整數微分的差分近似遞推式求極限推演而推廣到分數。其定義如下[5]:
如函數 f (t)∈(a, t)(a 從信號處理的角度看,信號的分數階微分的物理意義可以理解為廣義的調幅調相,其振幅隨頻率呈分數階冪指數變化,相位是頻率的廣義Hilbert變化。圖1示出1階、2階和分數階微分的幅頻特性曲線[6]。 從圖1中可以看出微分運算都有提升信號高頻的作用,且隨頻率和微分階數的增加呈非線性急速增長,同時對信號的甚低頻有削弱作用。從圖中明顯看出 2階微分對信號高頻成分的提升遠大于1階微分,且對甚低頻信號的削弱也明顯強于1階微分。對于分數階微分當0 圖1 信號微分的幅頻特性曲線 表明分數階微分在加強信號高中頻成分的同時,也對信號的甚低頻成分進行了非線性保留。對于圖像而言,平滑區域即鄰近的像素值基本相同的區域對應于信號的低頻;圖像紋理區域即鄰近的像素值發生一定變化的區域對應于信號的中頻;圖像邊緣和噪聲區域即鄰近的像素值發生較大變化的區域對應于信號的高頻。從圖中同樣可以看出當微分階數減小到0.1階后,微分運算對信號高頻的提升和信號中頻的加強幅度都不是很大。 一般來說,在采集到的路面圖像中包含兩類對象:一是狀況良好的路面,即背景;另一個是裂縫等病害,即識別的目標。因此,數字圖像可分為兩類像素集:代表背景的像素和代表裂縫等病害的像素。理想狀況下,裂縫應該比背景更暗。但是由于許多因素的影響,會有所變化。具體的情況有: (1)由于路面材料的不均勻性,正常路面的紋理不均勻。因此,所采集的圖像背景顏色本身有較大地變化。 (2)裂縫圖像也有同樣的情況。由于嚴重程度不同,其大小、面積也不同。如果裂縫中有與背景顏色相近甚至更亮的比較大的顆粒,也會導致裂縫圖像顏色的變化。但總的來說,裂縫圖像比正常路面的暗。 (3)代表裂縫的像素數量遠遠小于代表背景的像素數量。 (4)正常路面的灰度值與裂縫的灰度值有部分重疊。 (5)由于自然和人為因素的影響,復雜的背景噪聲一般都疊加在有用的路面數據之中,所以必須進行濾波來減少噪聲,增強裂縫邊緣。 基于以上這些路面圖像特性,可以采用有針對性的處理方法。本文從分數階微分差值定義著手,構建了適合路面圖像增強的分數階微分掩模算子,通過中值濾波去除孤立噪聲,最后利用形態學算子檢測出裂縫。 2.1.1 分數階微分差值定義 根據式(1),若一元信號f (t)的持續期為t∈[a,t],將信號持續期[a, t]按單位等分間隔h=1進行等分,所以可以推導出一元信號f (t)分數階微分的差值表達為式(3)所示。 對數字圖像f (x, y),其偏分數階微分為式(4)和式(5)所示。 2.1.2 路面圖像的分數階微分掩模運算 二維數字圖像信號中x和y的持續期間分別為x∈[x1, x2],y∈[y1, y2],對圖像的分數階微分運算從水平、垂直和斜向45o方向進行。根據式(4)和式(5)構造濾波器,獲得3*3、5*5、7*7,…,(2*n+1)*(2*n+1)等尺寸的八方向分數階微分算子。 本文使用了5*5的分數階微分掩模算子如圖2所示,對圖像進行空間濾波處理,掩模中的元素值為v的一元二次表達式,將掩模的每個元素都除以16*v*v-48*v+ 32。設m(i, j)為掩模中位值為(i, j)的元素,f (x, y)為掩模作用于圖像的中心像素,f (x+i, y+j)為距離中心(i, j)的像素,故可以得到掩模的運算規則為 圖2 5*5微分掩模 移動掩模使作用于圖像的每一個像素,從而達到圖像增強的目的。當像素距離圖像邊緣小于兩個像素時,掩模不能完全覆蓋到圖像上,此時則不進行運算。 常用而且有效的孤立噪聲的消除是中值濾波法,如式(7)所示 其中 med()為集合{X(s, t)}的中值函數,X(s, t)是n*n窗口內的像素。 它把鄰域中的圖像的像素按灰度級進行排序,然后選擇該組的中間值作為輸出像素,所以中值濾波對極限像素值不敏感,從而可以消除孤立的噪聲點,又可以使圖像產生較少的模糊。 形態學是一門建立在嚴格的數學理論基礎上的科學,它利用集合論的方法對物體的幾何結構進行分析和處理。在圖像分析與處理領域中,將形態學推廣至灰度形態學,使用具有一定形態的結構元素來度量和提取圖像中的對應的形狀,從而達到對圖像進行檢測和識別等目的。形態學的基本操作有腐蝕、膨脹、開運算、閉運算、擊中擊不中變換等,具體請參考相關文獻[7]。 膨脹運算一般是給圖像中的對象邊界添加像素,進行膨脹運算時,輸出像素值是輸入圖像相應鄰域內所有像素的最大值。用結構元素b對輸入圖像f進行灰度膨脹如下式所示 其中 DfDb分別是f和b的定義域。 腐蝕運算是刪除圖像邊界元素,輸出像素值是輸入圖像相應像素鄰域內所有像素的最小值。用結構元素b對輸入圖像f進行灰度腐蝕如下式所示 細化就是把輸入的具有一定寬度的圖像輪廓用逐次去掉邊緣的方法最終變為寬度僅為一個像素的骨架,通過細化可以顯示圖像的拓撲結構,細化通過兩步腐蝕如公式來實現。 (1)選擇圖2所示的5*5分數階微分掩模算子,為了便于后續檢測工作中閾值的設定,將算子的每一項都除以32-48*v+16*v*v,其中v是分數階微分算子的分數階數,取 v=0.7(分數階微分算子具有微分可調的特性,調節分數階微分的分數階數可以改變輸出像素的變化程度,很容易調節圖像的銳化效果,在實驗中v=0.7取得了較好的實驗效果)。 (2)將第一步運算后所得算子根據式(7)所示的掩模與路面病害圖像運算,注意當像素距離圖像邊緣小于兩個像素時,掩模不能完全覆蓋到圖像上,此時則不進行運算。 (3)把第二步演算后得到的圖像的像素值與原圖像對應像素相減得到圖像的病害邊緣信息。 (4)將經過上述增強的圖像再實施組合中值濾波,濾除孤立噪聲點。 (5)組合使用圖像形態學的膨脹腐蝕等算子,提取出路面圖像的裂縫。 實驗用計算機為 CPU Intel Pentium IV 2.93GHz處理器、1G內存,80G硬盤,編程工具選用Matlab7.0.4。原始圖像來自滬寧高速實拍圖片,處理圖像的尺寸為256*256像素。利用本文算法,對大量圖像進行了實驗,這里給出有代表性的路面病害圖像,圖3幾種算子對含有較弱信號縱向裂縫的增強結果比較、圖4、圖5幾種算子對縱橫交錯裂縫的增強結果比較以及用本文算法進行增強,中值濾波和用形態學算子提取裂縫的結果。圖6是網狀裂縫的增強結果及裂縫的標出結果。 圖3、圖4、圖5和圖6中(a)為原輸入圖像,圖3、圖4和圖5中 (b)、(c)、(d)、(e)是幾種經典算法和本文提出算法的比較。其中(b)、(c)為經典1階Sobel、Prewitt算子演算的結果,(d)為2階的Laplacian of Gaussian(Log)算子演算的結果,(e)為分數階數為0.7的分數階微分算子演算后的結果。從圖中可以看出,1階Sobel和Prewitt梯度算子演算結果比較接近,2階Log算子演算的結果與本文有些相似。但是,對原圖像用幾種經典算法演算后得到的結果與本文提出的方法演算后得到的病害圖像結果相比,圖(e)的病害信息更加清晰,而且保留了更豐富的弱信號信息即對弱信號病害部分的增強比其余算子顯著增強。 圖3 幾種算子對縱向裂縫增強演算結果比較 圖4 增強演算結果比較及用本文算法提取裂縫 圖5 幾種算子演算結果比較及用本文算法提取裂縫 圖6 網狀裂縫的增強及裂縫的標出結果 圖3所示為含縱向弱信號裂縫圖像增強。圖(e)中弱信號裂縫對比度增強,而且比(b)、(c)、(d)保留了更豐富的弱信號信息。圖4所示為復雜裂紋圖像增強與檢測。圖(e)獲得的病害信息更加清晰,而且依然保留了更豐富的弱信號信息。圖4和圖5中(f)、(g)、(h)分別為用本文算法進行二值化,組合中值濾波及用形態學算子實現的裂縫提取結果。圖6中(b)為本文算法實現的增強結果,(c)為最終檢測到的病害圖像,其中病害部分用紅色線條標出。 經過大量的實驗說明,本算法對于路面圖像中弱信號病害的增強效果顯著。雖然,本文所采用的算法比傳統的方法有很大的改進,病害檢測也非常有效,但是,也注意到對于有大量較暗的離散顆粒的圖象處理效果還存在缺陷,如圖 6(c)中的離散紅色點,同時也發現由于攝像機的采光問題導致對于背景光分布特別不均勻的圖像會存在誤測情況,這也正是后續研究工作的重點之一。 通過分析信號經過微分后的幅頻特性,得出基于分數階微分的圖像增強算子比傳統的基于1階和2階的微分算子具有更高的清晰度,尤其是在平滑區域。根據經典的分數階微分G-L定義推導出的分數階微分的差分定義,構建了分數階微分掩模,通過分數階微分掩模運算增強路面圖像,使處于平滑區域的弱信號裂縫病害信息有效加強。 實驗結果表明,本文提出的分數階微分掩模有很好的圖像弱信號增強功能。通過與其它空間濾波算子的效果比較,可以看出,本文設計的分數階微分算子彌補了傳統圖像增強算子不能通過改變參數來得到連續變化的增強效果,以及對于較弱信號增強效果不理想的缺陷。同時,自適應閾值的選擇也在很大程度上提高了病害檢測的效果。由實驗結果可以得出結論,基于分數階微分的病害圖像處理方法效果良好,而且,算法更具靈活性和針對性。該方法可以廣泛應用于路面圖像病害檢測。盡管如此,在實驗中還是發現對于紋理過于粗糙的圖像的處理效果欠佳,存在較多密集的離散點,還存在進一步改進的空間,在后續研究工作中一方面要尋求普遍自適應閾值選取方法;另一方面可以在線條擬合方向展開。 [1]張洪光, 王 祁, 魏 瑋. 基于人工種群的路面裂紋檢測[J]. 南京理工大學學報, 2005, 29(4):389-393. [2]高建貞, 陸建峰, 趙春霞, 等. 基于多級擬合的道路病害自動檢測與識別[J]. 計算機工程與應用, 2004,22: 220-223. [3]唐 磊, 趙春霞, 王鴻南, 等. 基于圖像三維地形模型的路面裂縫自動檢測[J]. 計算機工程, 2008, 34(5):21-38. [4]王 剛, 賀安之, 肖 亮. 基于高速公路裂紋局部線性特征內容的脊波變換域算法研究[J]. 光學學報,2006, 26(3): 341-346. [5]Pincherle I. Fractional differential equations [M]. San Diego: Academic Press, 1990. 20-23. [6]蒲亦非. 將分數階微分演算引入數字圖像處理[J].四川大學學報(工程科學版). 2007, 39: 124. [7]阮秋琦. 數字圖像處理學[M]. 北京: 電子工業出版社, 2001. 430-450.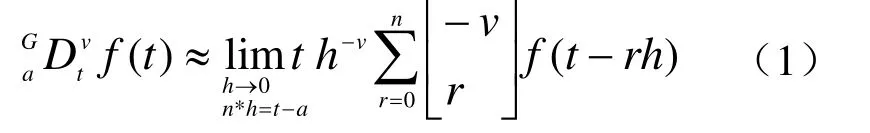
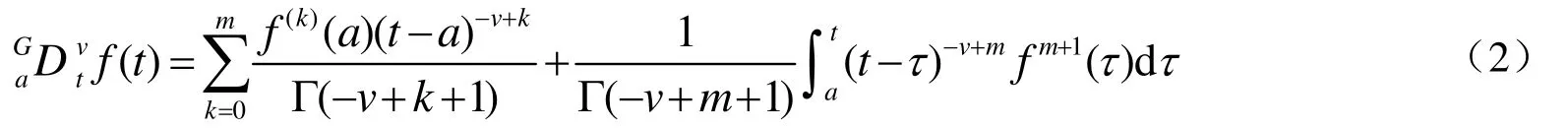
1.2 分數階微分運算用于圖像信號處理

2 構建分數階微分掩模算子實現路面裂縫檢測算法
2.1 構建分數階微分掩模算子
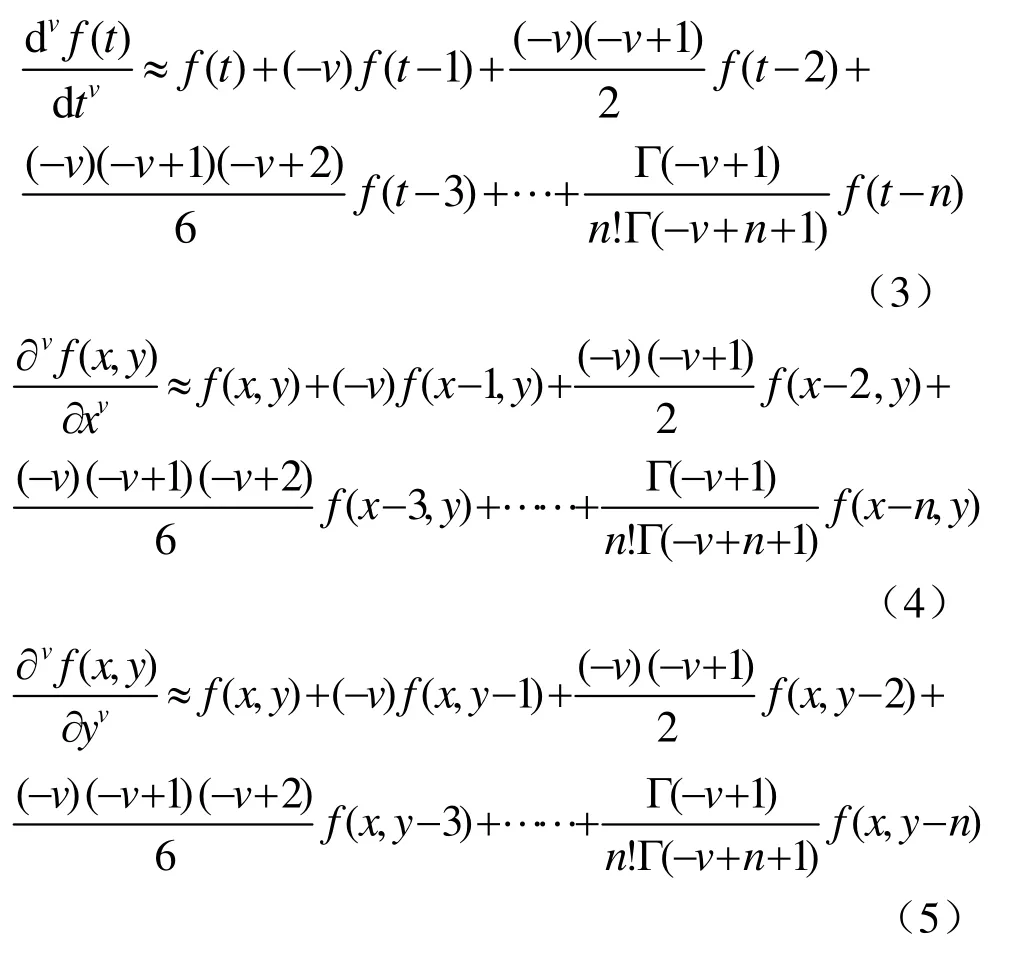


2.2 中值濾波去除孤立噪聲
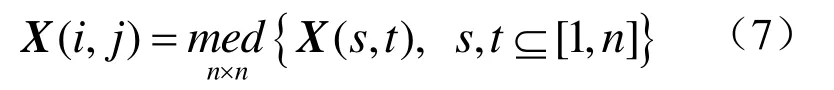
2.3 形態學演算實現路面裂縫提取
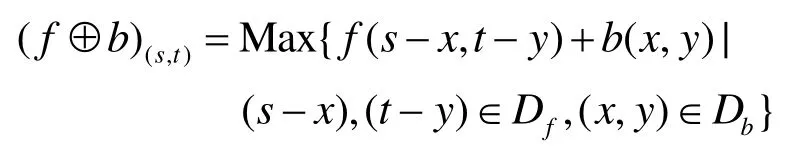
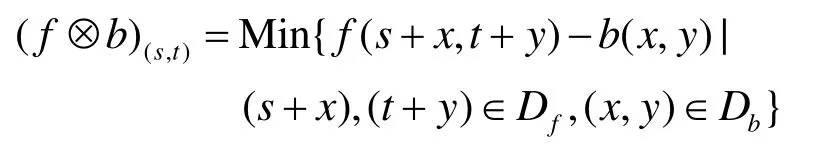
3 實驗結果
3.1 實驗過程
3.2 結果分析




4 結 論

