隨機條件下固定公交線路服務頻率優化模型＊

陳維亞 陳治亞

（中南大學交通運輸工程學院1） 長沙 410075） （西安電子科技大學2） 西安 710071）

0 引 言

根據公交線路的乘客需求合理確定公交線路服務頻率是平衡公交供求的關鍵內容.在實際的公交服務中，線路服務頻率越高，乘客在站候車時間可能越短，并且獲得座位或者能夠上車的可能性越大，但是對于公交部門可能意味著較低的車輛利用率和較高的運營成本；而服務頻率越小，公交車輛利用率可能越高，但乘客等車時間可能越長甚至由于車輛滿載而無法上車.

在已有的確定公交線路服務頻率的模型中，以文獻［1－3］為代表的模型均以縮短乘客候車時間和降低車內擁擠程度為乘客滿意目標，以公交線路收益最大為企業滿意目標，通過雙層規劃或者加權組合等方式以期獲得總體最佳的服務頻率.這些模型雖然都綜合考慮了乘客利益和公交公司的效益，但是都假設車輛在站間區間的運行速度為定值，因而忽略了實際運營過程中車輛站間運行時間的隨機性以及由這種隨機性導致的車輛載客不均勻性.針對這個問題，本文考慮車輛站間運行時間的隨機性和乘客需求的波動性以及二者的相互動態影響，建立了以乘客候車期望和公交車輛利用率總體最優為目標的公交服務頻率優化模型.鑒于公交服務過程的動態隨機特性，利用蒙特卡羅方法對模型進行模擬求解.

1 模型建立

1.1 模型假設

由于公交線路服務除了受到車輛站間運行時間隨機性和乘客需求波動性等復雜特性影響之外，還受到許多其他因素的影響，為了有針對性的對所研究問題進行探討，在建立模型之前，需要結合實際對被考察公交線路作如下假設：（1）被考察線路為高頻服務線路，發車間隔小于10min［4］（在這個假設下認為乘客隨機到站比較合理），且在同一時段內從始發站出發的時間間隔不變，即服務頻率不變.（2）乘客到站服從一定的概率分布，并且先到先服務，沒有得到服務的乘客在下趟車優先服務.（3）車輛到站后，下車乘客人數與到站時的車上總乘客數成正比.（4）不同車輛在相同站間的運行時間呈同一概率分布，不同趟次的車輛運行相互獨立.（5）平均每位乘客的上下車時間為常數，車輛在車站的等待時間由乘客上下車時間決定.（6）同一線路上的車輛的承載能力相同且為定值.

1.2 變量和符號說明

為了更清晰的表達所描述的問題，首先定義以下變量和參數：i為下標變量，表示車輛發車順次，i＋1代表緊隨i后的車輛；k為下標變量，表示公交車站站序，約定始發站為0，然后依次為1，2，3，…；H為始發站固定發車時間間隔；Hik為車輛i與前一輛車（i－1）到達車站k的實際車頭時間距；Rik為車輛i從車站（k－1）啟動運行至車站k停車的時間；Dik為車輛i在車站k服務乘客上下車的等待時間；Aik為車輛i到達車站k時車上需要下車的乘客數；Bik為車輛i到達車站k時上車的乘客數；UBik為車輛i離開k站時由于車輛滿載未能上車的乘客數；Lik為車輛i離開車站k時車上乘客總數；α為乘客平均下車時間；β為乘客平均上車時間；λk為車站k的乘客到達率；ρk為車輛到達車站k時將要下車乘客占車上總乘客的比率；C為車輛的承載能力.

1.3 模型建立

乘客候車期望體現為較短的候車時間和舒適的乘車環境，至少車輛到站后可以順利上車而不用等待下一趟車.車輛利用率表現為平均線路斷面載客量，平均線路斷面載客量越大，車輛利用率越高.由此建立如下的公交線路服務頻率優化模型

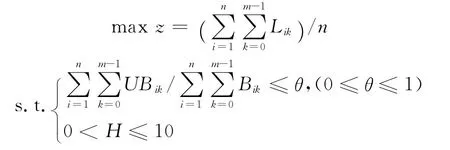
模型中，目標函數為獲得最大平均線路斷面載客量，第一個約束條件表示線路各站由于車輛滿載未能上車而必須繼續等待的乘客總數占所有上車的乘客數的百分比必須小于某一乘客候車期望衡量標準θ，這個約束條件體現了乘客候車期望，θ越小，表示乘客候車期望越高，它在一定程度上綜合了文獻［3］中的候車滿意度與舒適滿意度.第二個約束條件滿足假設（1）中的高頻線路要求.

1.4 模型分析

模型中的目標函數和第一個約束條件需要逐車逐站計算斷面載客量、上車乘客數和未上車乘客數，這可以通過分析公交服務過程中乘客與公交車輛的動態互動關系得到.

對于高頻發車的公交線路，多數文獻都證實乘客到站和下車人數通常服從一定的概率分布.本文假定乘客到站服從Poisson分布且平均乘客到站率為λk（人／min），下車乘客人數服從二項分布且下車人數占車上總人數的比率為，乘客上車與下車同時發生，則車輛到達車站服務乘客上下車所用的等待時間Dik是乘客總下車時間和總上車時間中的較大值，即

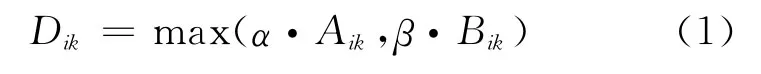
式中：max（）表示取括號中二者的較大值，Aik和Bik可分別通過下式計算得到

此時，可能由于車輛滿載未能上車的乘客數為

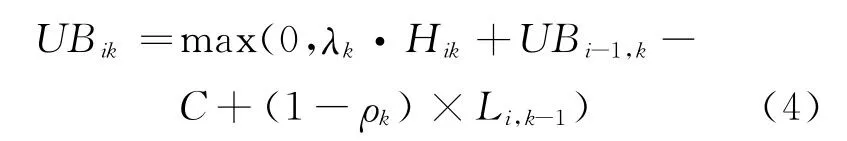
車輛離開車站時的總乘客數為

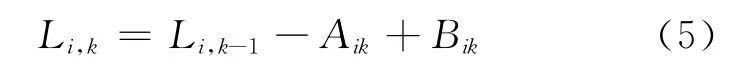
考慮到站間運行時間隨機性和乘客需求波動性，因此在始發站發車間隔一定的情況下各站的車頭時間距會隨車輛運行而改變，以上公式中的變動車頭時間距為

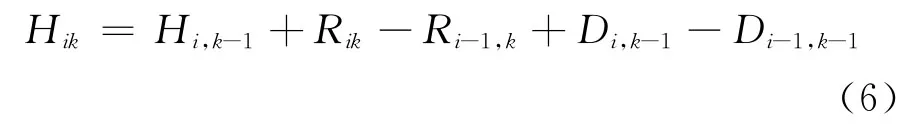
由于Hik被定義成車輛i與前一輛車（i－1）到達車站k時的車頭時間距，因而忽略了乘客上下車時間內乘客的進一步到達對問題的影響.式（6）中的站間運行時間可以根據假設（4）通過一定的概率函數獲得.

1.5 模型求解

由上述公交服務過程分析可以看出，計算公式具有傳遞性和迭代性，可在給定初始狀態的情況下遞推得到逐車逐站的斷面載客量、上車乘客數和未上車乘客數.在上述隨機條件下的公交服務過程可用蒙特卡羅（Monte－Carlo）方法進行模擬［6－8］.在給定線路參數條件下，目標函數和約束條件均為車頭時間距的一元函數，且目標函數中最大化平均線路斷面載客量要求發車間隔趨向于越大，因此可以采用如下步驟對模型進行近似最優求解.

步驟1根據不同線路情況初始化線路基本參數.

步驟2設定最大發車間距H＝10min和服務時段長度.

步驟3運用蒙特卡羅方法模擬時段長度內的服務過程并計算目標函數和第一個約束條件.

步驟4檢驗約束條件，若約束條件被滿足，得到近似最優發車間隔和頻率，結束搜索；否則轉步驟5.

步驟5以步長s遞減調整起始站發車間隔，轉步驟3.

2 應用實例與結果

2.1 線路基本參數

考慮一條固定公交運營線路，從出發站到終點站均勻分布有11個停靠站（k＝0，1，2，…，10），2個站間的運行時間獨立同分布，且服從正態分布N（μ，σ2），站間期望運行時間均為3min，考慮到不同的路段路況差異，運行時間方差將設置不同.停靠站的等待時間根據各站的乘客需求決定，每個乘客的平均上車時間為3.0s，每個乘客的平均下車時間為1.8s，即α＝0.05，β＝0.03.從始發站按規定的發車間隔H發出一輛公交車，服務時段設為早高峰06：30～09：00，公交車的容許承載人數為C＝80人.表1給出了試驗線路的乘客需求和路段運行時間參數.

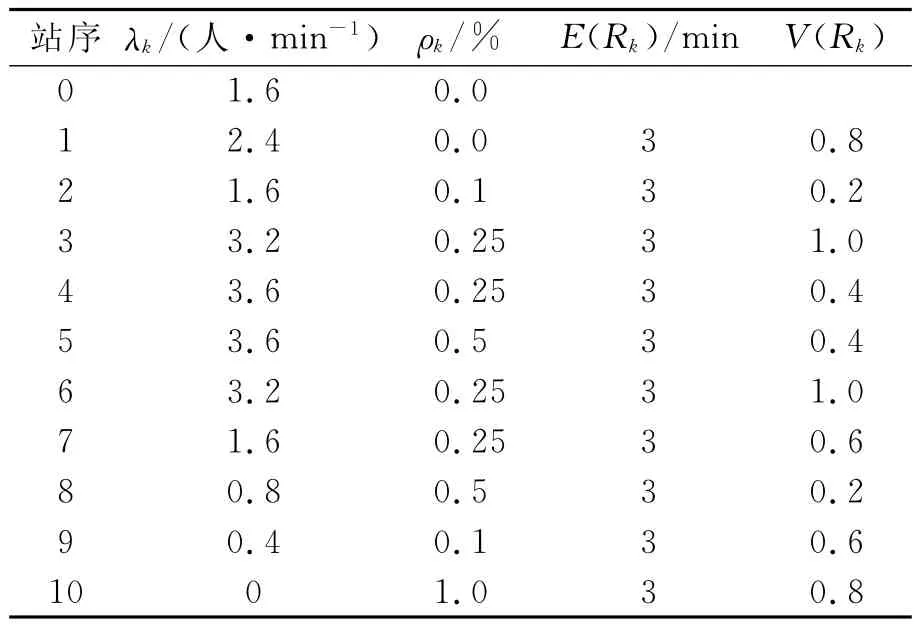
表1 實驗公交線路參數

2.2 計算結果

給定乘客對此實驗線路的候車期望為θ＝1%，迭代步長為10s，利用蒙特卡羅方法在EXCEL中對前面描述的公交服務過程進行了隨機模擬，并計算得到了最優發車時間間隔，表2給出最后5次迭代的結果.

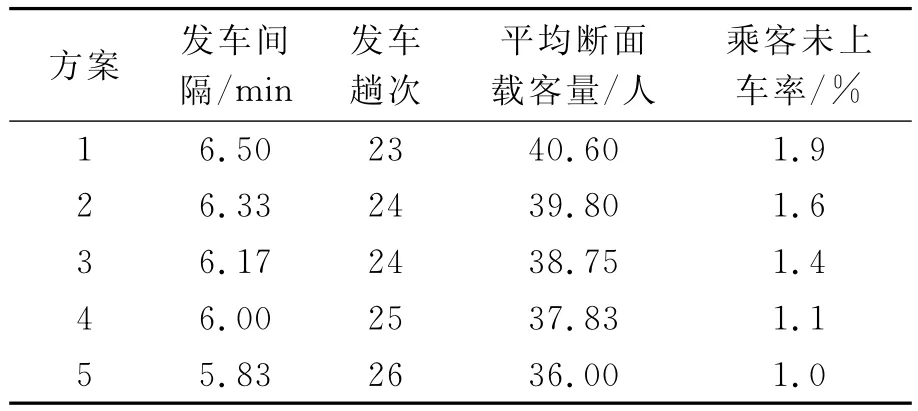
表2 發車間隔及乘客候車期望和車輛利用率

3 結 論

本文建立的固定公交線路服務頻率優化模型綜合考慮了公交服務過程中的車輛站間運行時間隨機性和乘客需求波動性以及二者的相互動態影響，以乘客候車期望和公交車輛利用率總體最優為目標兼顧了乘客和公交公司利益，符合公交調度決策的思路.

利用了蒙特卡羅方法將隨機乘客需求和隨機車輛運行時間運用到模型求解過程中，比較真實地反映了公交服務過程，能夠計算得到公交供求平衡狀態下的最優服務頻率.

需要指出的是，基于模型的假設和仿真求解過程，本模型只適用于高頻服務公交線路.同時，在實際運用中，在給定車輛載客能力的情況下，如果線路上乘客需求過大，理論上能夠找到夠小的發車間隔時間，但現實中可能通過增大車輛載客能力來解決過大的乘客需求.

［1］朱金壽，朱 琪，楊永剛，等.公交車調度方案的研究［J］.武漢理工大學學報：交通科學與工程版，2002，26（2）：169－171.

［2］呂 鵬，張文夫，雷 鵬.公交車調度問題［J］.工程數學學報，2002，19：75－80.

［3］牛學勤，陳 茜，王 煒.城市公交線路調度發車頻率優化模型［J］.交通運輸工程學報，2003，3（4）：69－72.

［4］Transit capacity and quality of service manual（［M］.2nd.TCRP Report＃100）［EB／OL］.［2009－04－08］.http：／／www.trb.org／news／blurb＿detail.asp？id＝2326，2004－01－27.

［5］Hickman M D.An analytic stochastic model for the transit vehicle holding problem ［J］.Transportation Science，2001，35（3）：215－237.

［6］Moses I E.A transit route simulator for the evaluation of control strategies using automatically collected data［D］.Cambridge：Massachusetts Institute of Technology，2005.

［7］司徒炳強，靳文舟.合作與競爭條件下公交網絡發車時間優化模型［J］.公路交通科技，2010（6）：48－51.

［8］蘆方強，陳學武，陳素平.基于成本分析的快速公交發車頻率優化方法［J］.東南大學學報：自然科學版，2009（4）：55－58.