交通信息對駕駛員逐日路徑選擇行為影響研究＊

劉詩序 關宏志 嚴 海

（北京工業大學交通工程北京市重點實驗室 北京 100124）

對不同交通信息條件下駕駛員的逐日路徑選擇行為，國內外學者做了一些研究.Cantarella和Cascetta［1］建立了逐日路徑選擇模型，指出駕駛員個人經驗可以穩定網絡交通流，并且信息的發布使網絡交通流不穩定.Nakayama和Kitamura［2－4］基于人是有限理性的假設，建立駕駛員的路徑選擇模型，并通過蒙特卡羅仿真得出：路網最終的收斂狀態不一定趨于Wardrop用戶均衡.Chen等人［5］考慮出行需求、駕駛員對行程時間初始值的不確定性、學習方法和風險等因素，基于微觀Agent模型對假設路網進行仿真.Selten等人［6］基于實驗的方法，以18個大學生為對象，研究了出行者的路徑選擇行為，并建立一個簡單回報總和增強模型，對出行者路徑行為進行模擬實驗分析.Kim等［7］運用逐日演化方法，研究了用戶平衡假設條件對網絡交通流的作用.劉天亮和黃海軍［8］基于多智能體環境SeSAm，對交通信息公開和不公開兩種路徑更新規則進行了模擬研究.在預測信息條件下，Klügl和Bazzan［9］基于 Agent仿真環境SeSAm，研究了駕駛員的日常路徑選擇中的學習行為，定義了一種啟發式的更新規則來模擬駕駛員的路徑選擇.本文設計一種實際可行的信息預測方法，針對3種信息條件：無信息、歷史信息、預測信息，以駕駛員個體為對象，將每個駕駛員看成一個Agent，運用Agent仿真思想，對駕駛員逐日路徑選擇行為進行數值仿真，探索駕駛員行為的整體涌現特征，以用戶均衡狀態為基準，比較3種信息的效果.

1 駕駛員逐日路徑選擇過程

本文假設駕駛員逐日路徑選擇過程如圖1所示.首先，駕駛員獲取路網信息，包括路網行程時間信息以及交通系統發布的信息（如果有出行信息），然后，駕駛員根據這些信息估計下一天路徑的行程時間（即理解行程時間），駕駛員再根據理解行程時間和一定的規則進行路徑選擇.本研究假設路網中所有駕駛員同時出發，即同時選擇路徑，所有人選擇完路徑后更新路網信息，駕駛員根據新的路網信息再次出行.

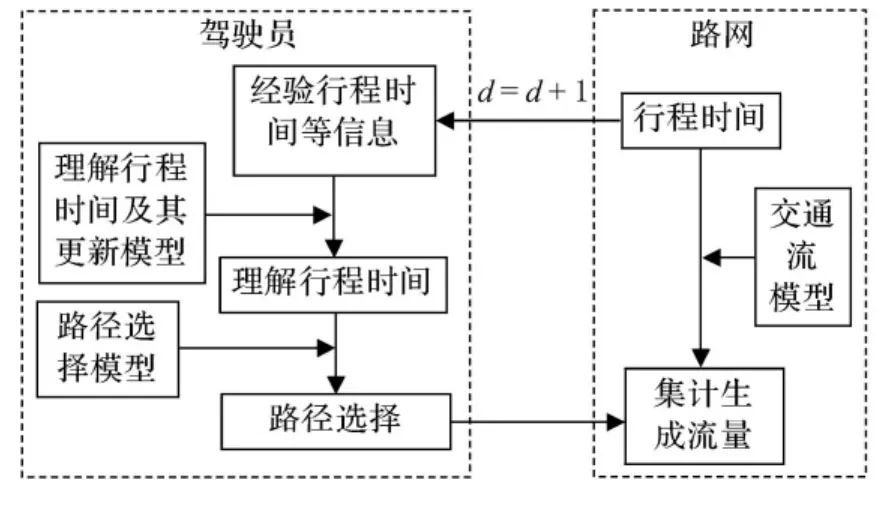
圖1 駕駛員路徑選擇過程

2 模 型

在現實中，由于不確定因素駕駛員不可能精確地提前預知路徑的行程時間，駕駛員只能根據理解行程時間選擇路徑，出行者i在第d天對路徑k的理解行程時間為

假設隨機項ξ服從均值為0的Gumbel分布是出行者i在第d天對路徑k理解行程時間的期望值.隨機項ξ與時間、具體路徑無關，其大小反映駕駛員對路網的認知程度.假設rs之間有n條路徑，根據隨機效用理論，個人效用最大化原則，那么，出行者i在第d天對路徑k的概率為

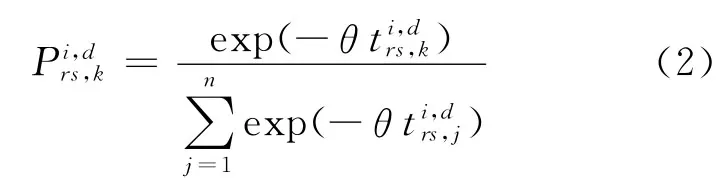
式中：θ為駕駛員路徑選擇的隨機程度，與行程時間隨機項ξ的方差相關，θ越小，ξ的方差越大.可以解釋為，駕駛員路徑選擇的隨機程度越大，反之，θ越大，駕駛員路徑選擇的隨機程度越小.在仿真時，駕駛員路徑選擇規則使用輪盤賭方法［8］，概率較大的選擇的傾向較大，方法如下：假設駕駛員i有n條可選路徑，通過式（2）計算出每條路徑的概率分別為p1，p2，…，pn，運用計算機的隨機數發生器產生隨機數a，若駕駛員i選擇路徑k，同時路徑k的流量增加一個單位.

駕駛員選擇路徑的概率與理解行程時間的期望值相關，下面對無信息、發布歷史信息、發布預測信息3種情況，分別建立理解行程時間期望值的更新模型.

1）無信息條件下的更新模型 出行者信息系統不發布任何信息，駕駛員只能根據自己的歷史經驗獲取下一天的理解行程時間，第d＋1天的理解行程時間期望值表示為第d天期望時間和實際時間的加權平均，未經歷路徑的理解行程時間期望值不變，更新模型

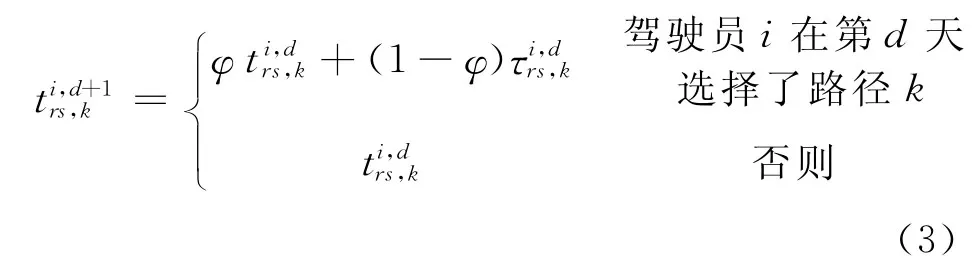
式中：ti，d＋1rs，k為出行者i在第d＋1天對路徑k理解行程時間的期望值為出行者i在第d天對路徑k理解行程時間的期望值為出行者i在第d天經歷的路徑k的實際行程時間；φ為權重系數.φ的大小反映出行者對前一天的實際行程時間（經驗）的依賴程度，φ越大，依賴程度越小，反之，φ越小，依賴程度越大.

2）發布所有路徑歷史信息條件下的更新模型 當出行者信息系統發布所有路徑的歷史信息時，第d＋1天的理解行程時間期望值根據第d天期望時間和實際時間更新

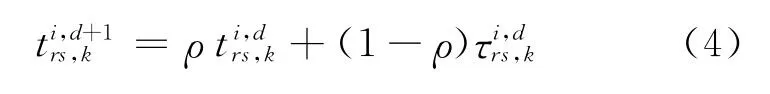
式中：ρ為權重系數.其他符號意義同前.權重系數ρ的意義和φ相同，ρ越大，出行者對前一天的實際行程時間（經驗）的依賴程度越小，反之，ρ越小，依賴程度越大.

3）發布所有路徑的預測信息條件下的更新模型 出行者信息系統發布預測信息時，第d＋1天的理解行程時間期望值根據第d天期望時間和預測時間更新

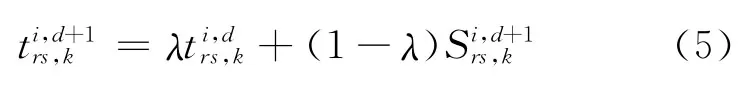
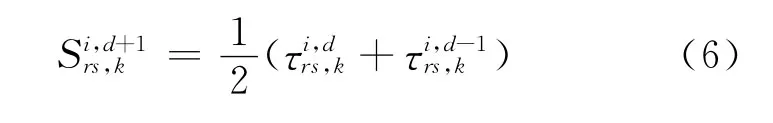
由于第1天駕駛員沒有歷史經驗，第1天的理解行程時間期望值初始化為自由流行程時間.當發布信息為預測信息時，第2天的理解行程時間期望值取為第1天實際行程時間，從第3天開始采用式（5）更新.

駕駛員路徑選擇集計到路網上就生成流量，使用BPR函數可以計算得到路徑的行程時間.

3 仿真實驗

3.1 場景設計

如圖2所示，仿真使用2條平行路徑的簡單路網，路徑的行程時間t＝tf［1＋0.15（q／C）4］，其中：tf為路徑的自由流行程時間；q為路徑流量；C為路徑通行能力，輛／h.路徑1的自由流行程時間tf1＝22min，通行能力C1＝150輛／h，路徑2的自由流行程時間tf2＝25min，通行能力C2＝200輛／h.可以看到，路徑1路程短，但是容量小，路徑2路程長，但是容量大.駕駛員數量為200個，這些駕駛員每天在這兩條路徑出行一次，路網達到用戶均衡時，路徑1的流量為146.7輛／h，路徑2的流量為53.3輛／h.設仿真天數為1 000d，對這200個駕駛員每天的路徑選擇進行仿真實驗.

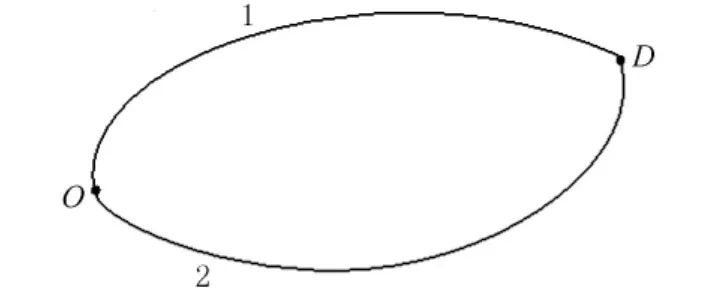
圖2 路網示意圖

3.2 仿真結果分析

運用 MATLAB軟件，對參數θ，φ，ρ和λ不同取值情況分別進行仿真實驗，考察在3種交通信息條件下，路徑流量的變化情況.以最后100d路徑1上流量的均值和標準差為統計量，經過若干次仿真實驗，發現θ＝0.4是駕駛員路徑選擇隨機程度的一個分界點，當θ小于0.4和θ大于0.4時，3種交通信息對駕駛員的路徑選擇影響不同，發布效果有明顯差異，取θ＝0.1，0.4和0.6情況分別闡述如下.

1）θ＝0.1時 以φ＝ρ＝λ＝0.01為例，3種交通信息條件下，路徑1和2的流量隨天數的變化情況見圖3.以最后100d路徑1上流量的均值和標準差為統計量，定量描述3種交通信息下流量的演化結果，統計結果見表1，可以看到，3種情況下路徑1流量的均值和標準差大小都相當，因此，3種信息對駕駛員的路徑選擇影響相近.

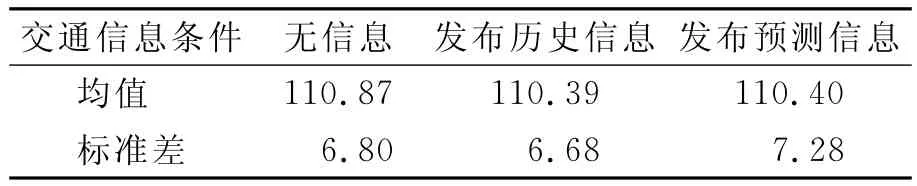
表1 θ＝0.1，φ＝ρ＝λ＝0.01時路徑1流量的均值和標準差 輛／h

改變參數φ，ρ，λ的值，計算最后100d路徑1上流量的均值和標準差，統計結果見圖4.

圖3 θ＝0.1時路徑流量均值隨時間的變化圖

圖4 θ＝0.1時路徑1的流量均值和標準差隨權重系數變化圖

從圖4可以看到，流量的均值和標準差隨權重系數變化不是很大，信息對駕駛員路徑選擇幾乎沒有影響.經過多次仿真發現，θ越小于0.4，3種信息對駕駛員的影響越相近.

2）θ＝0.4時 同理，統計參數φ，ρ，λ取不同值時最后100d路徑1上流量的均值和標準差，如圖5所示.

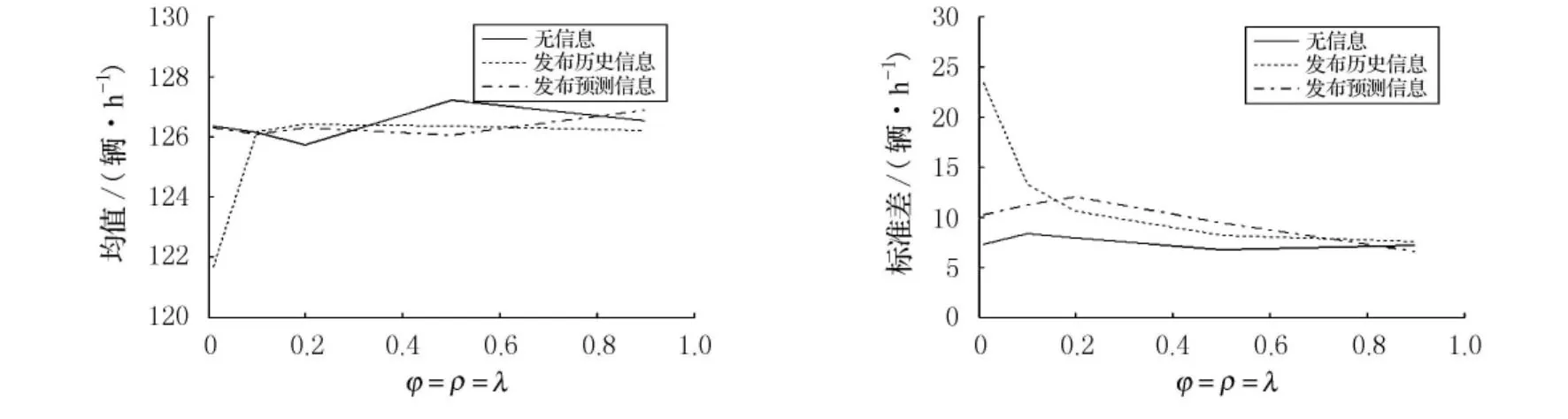
圖5 θ＝0.4時路徑1的流量均值和標準差隨權重系數變化圖

從圖5可以看到，發布預測信息和無信息情況類似，流量的均值和標準差幾乎不受權重系數的影響；發布歷史信息時，流量的均值和標準差隨權重系數變化較大.當權重系數較小時（≤0.1），即駕駛員對歷史信息和預測信息依賴程度較大（＞0.1），發布歷史信息條件下的流量均值較小，方差較大，這時發布信息的效果：無信息和預測信息相當，均比歷史信息好.權重系數較大時，即駕駛員對歷史信息和預測信息依賴程度較小，流量的均值和標準差變化趨勢基本相似，3種情況發布信息的效果相當.此時，與θ＝0.1時相比，流量均值增大，更接近用戶均衡狀態.經過多次仿真發現，θ取0.4附近的值，結論仍然成立.

3）θ＝0.6時 統計參數φ，ρ，λ取不同值時最后100d路徑1上流量的均值和標準差，如圖6所示.

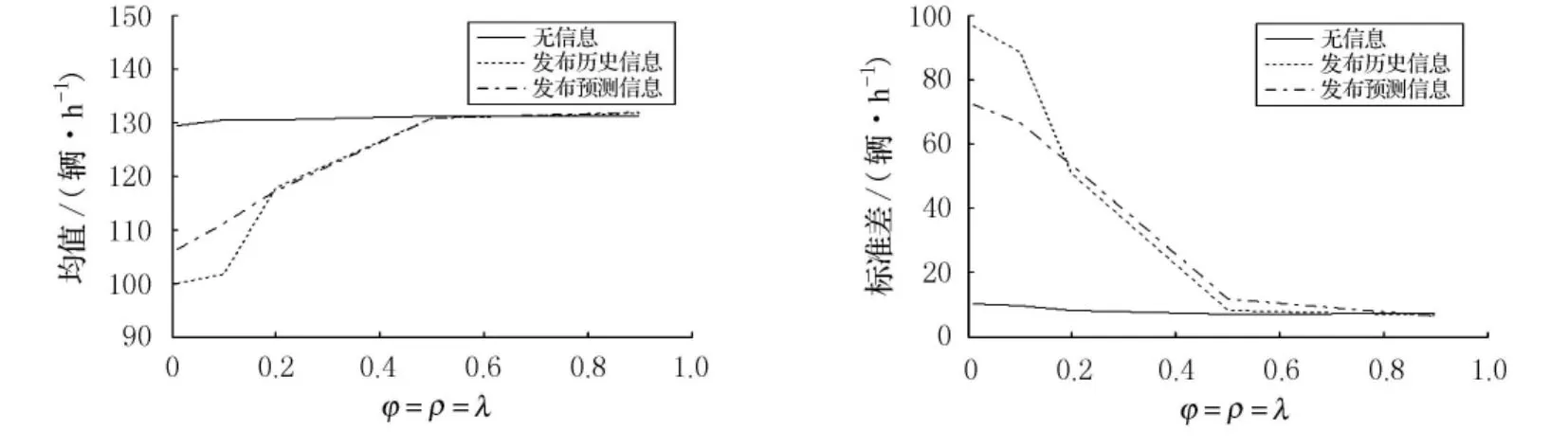
圖6 θ＝0.6時路徑1的流量均值和標準差隨權重系數變化圖

當θ＝0.6時，從圖可以看到，無信息情況下流量的均值和標準差隨權重系數變化較小；發布預測信息和歷史信息情況類似，流量的均值和標準差受權重系數的影響較大.當權重系數較小時（≤0.5），即駕駛員對歷史信息和預測信息依賴程度較大，流量的均值偏離用戶均衡狀態較遠，并且標準差較大.隨著權重系數的增大（＞0.5），3種信息情況越來越接近用戶均衡狀態.發布信息的效果：預測信息和歷史信息相當，均比無信息差.經多次仿真發現，θ越大于0.4，越明顯.

綜上，信息對駕駛員的影響呈現以下規律：隨著θ的增大，信息對駕駛員路徑選擇影響不同.θ較小時（≤0.4），即駕駛員路徑選擇隨機程度較大時（注意到參數θ的大小反映駕駛員路徑選擇的隨機程度），信息對駕駛員幾乎沒有影響，信息沒有起到作用.θ取0.4附近的值時，即駕駛員路徑選擇的隨機程度處于中間水平時，這時分兩種情況，如果駕駛員對歷史信息和預測信息依賴程度較大時，發布信息的效果是，無信息和預測信息相當，均比歷史信息好；如果駕駛員對歷史信息和預測信息的依賴程度較小時，3種信息的影響相近，信息沒有起到作用.θ較大時（＞0.4），即駕駛員路徑選擇的隨機程度較小時，信息發布效果是，預測信息和歷史信息相當，均比無信息差，信息反而起到“副作用”.

4 結 論

1）交通信息對駕駛員路徑選擇行為的影響與駕駛員路徑選擇的隨機程度以及駕駛員對信息的依賴程度有關.（1）駕駛員路徑選擇的隨機程度較小時，信息發布對駕駛員基本沒有影響，即信息沒有起到作用；（2）駕駛員路徑選擇的隨機程度處于中間水平時，如果駕駛員對歷史信息和預測信息依賴程度較大，發布信息的效果是：無信息和預測信息相當，均比歷史信息好，如果駕駛員對歷史信息和預測信息的依賴程度較小，3種信息的影響相近，信息沒有起到作用；（3）駕駛員路徑選擇的隨機程度較大時，信息發布效果是：預測信息和歷史信息相當，均比無信息差，信息反而起到“副作用”.

2）在3種交通信息條件下，路網均不能達到用戶平衡狀態.從流量的變化情況看，3種交通信息條件下，最后100d路徑1的流量均值與用戶平衡狀態時的流量有差別，并且流量呈現波動性，路網沒有達到平衡狀態.

3）如果交通信息的預測方法不同，預測信息對駕駛員的路徑選擇的影響有明顯差異.

對于實際的交通網絡（對應特定的模型參數θ和φ，ρ，λ），運用本研究方法即可確定3種交通信息對駕駛員路徑選擇行為的影響，因此，本研究對交通行為和ATIS的應用有參考價值.

［1］Cantarella G E，Cascetta E.Dynamic processes and equilibrium in transportation networks：towards a unifying theory［J］.Transportation Science，1995，29（4）：305－329.

［2］Nakayama S，Kitamura R，Fujii S.Drivers′learning and network behavior：a dynamic analysis of the driver－network system as a complex system［J］.Transportation Research Record：Journal of the Transportation Research Board，1999，1676：30－36.

［3］Nakayama S，Kitamura R.A route choice model with inductive learning［J］.Transportation Research Record：Journal of the Transportation Research Board，2000，1725：63－70.

［4］Nakayama S，Kitamura R，Fujii S.Drivers＇route choice rules and network behavior：do drivers become rational and homogeneous through leaning？［J］.Transportation Research Record：Journal of the Transportation Research Board，2001，1752：62－68.

［5］Chen R B，Mahmassani H S.Travel time perception and learning mechanisms in traffic networks［J］.Transportation Research Record，2004，1894：209－221.

［6］Selten R ，Chmura T，Pitz T，et al.Commuters route choice behaviour［J］.Games and Economic Behavior，2007，58：394－406.

［7］Kim H，Oh J S，Jayakrishnan R.Effects of user equilibrium assumption on network traffic pattern［J］.KSCE Journal of Civil Engineering，2009，13（2）：117－127.

［8］劉天亮，黃海軍.日常擇路行為的多智能體模擬［J］.物理學報，2007，56（11）：6 321－6 325.

［9］Klügl F，Bazzan A L C.Route decision behaviour in a commuting scenario：simple heuristics adaptation and effect of traffic forecast［EB／OL］.Journal of Artificial Societies and Social Simulation，［2004－01－31］http：／／jasss.soc.surrey.ac.uk／7／1／1.html.