不同溫度下瀝青混合料劈裂強度的影響因素＊

陸學元 張素云

（安徽省高速公路控股集團有限公司1） 合肥 230051） （安徽交通職業技術學院2） 合肥 230051）

0 引 言

瀝青混合料力學性能隨著溫度的變化表現非常復雜，當氣溫急劇降低，瀝青混合料剛性顯著增大，其模量遠大于半剛性基層模量，瀝青層底拉應力增大，在拉應力和剪應力的共同作用下行車帶輪跡邊緣附近容易產生拉裂，同時若溫度收縮應力超過瀝青混合料破壞強度路面將發生開裂［1－2］；高溫狀態下瀝青混合料強度急劇衰減，在車輛荷載作用下，路面產生水平應力超過瀝青混合料抗剪強度易出現車轍、變形等病害［3］.可見，瀝青混合料強度直接影響瀝青路面的路用性能與使用壽命.國內外學者從不同角度研究探討了瀝青混合料劈裂強度及其劈裂強度對路用性能的影響問題［4－6］.以往的研究對表面層瀝青混合料劈裂強度探討較多，對AC－25熱拌瀝青混合料劈裂強度問題研究及其在不同溫度條件下的力學性能演變規律探討則很少.本文結合前人研究成果，探討涵蓋粗型和細型級配的AC－25瀝青混合料劈裂強度影響因素問題，以揭示不同溫度下AC－25瀝青混合料劈裂強度的影響規律，對提高道路的綜合路用性能提供借鑒指導作用.

1 試驗設計與試驗結果

粗集料為石灰巖，細集料為石灰巖機制砂，填料為礦粉；結合料采用70號A級瀝青.技術指標均符合文獻［7］要求.采用正交試驗設計方法.考慮5因素（分別以A，B，C，D，E表示）和5水平，因素水平選取見表1.每組級配通過率符合正交表L25（5）6規定要求，見表2.以馬歇爾成型為技術手段，成型溫度為（152±2.5）℃，理論最大相對密度由真空法實測得到.每組有效試件12個，每4個試件分別用于0，15，45℃劈裂試驗使用.劈裂試驗儀器為LDR－2型瀝青混合料凍融劈裂儀，技術參數為最大荷載50kN，荷載范圍5～35kN，加載速率為（50±5）mm／min，并配有試驗環境箱.按照規程方法試驗，結果見表2.

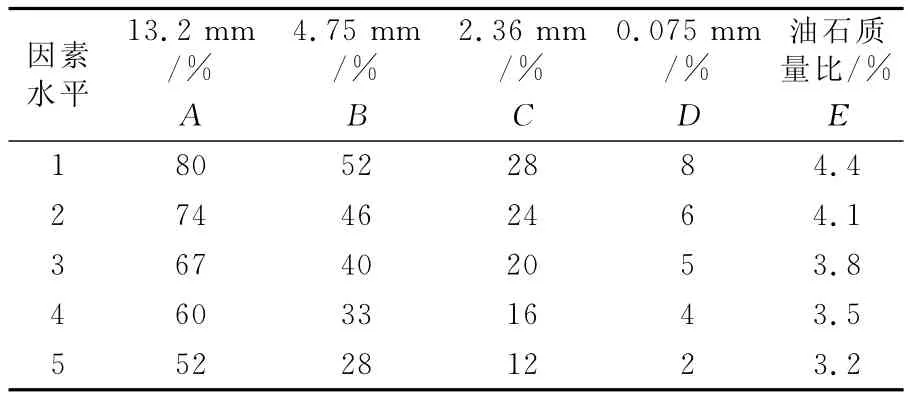
表1 正交試驗設計因素水平表

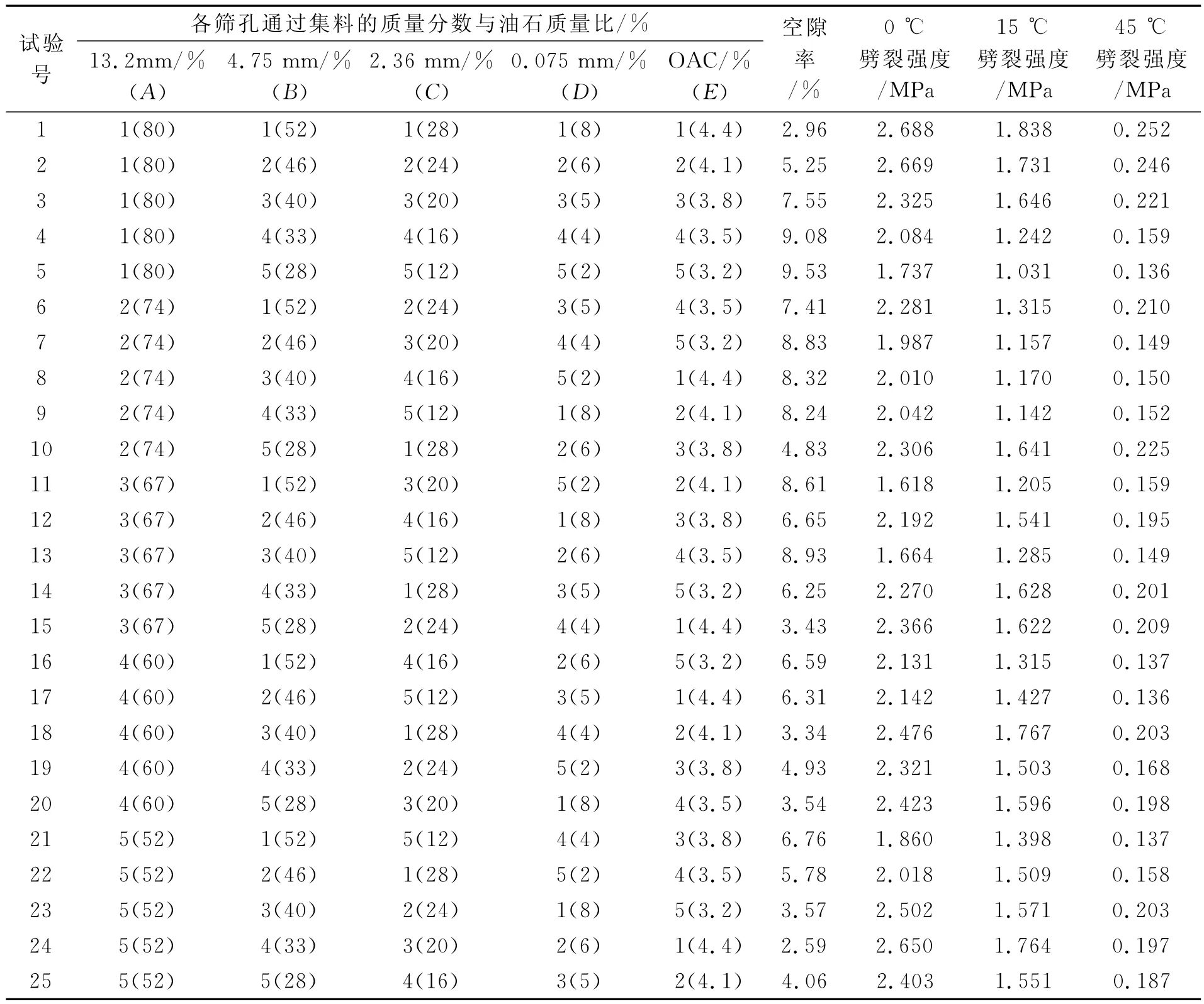
表2 設計方案與試驗結果

2 結果分析

2.1 方差分析

方差分析法是將因素水平變化引起的試驗結果間的差異與誤差波動引起的試驗結果間的差異區分開來的一種數學方法，可以對各因素的顯著性水平給出一個定量分析，基本過程如下.

檢驗各因素水平的變化是否對劈裂強度有顯著影響，是檢驗式（1）的假設.

對檢驗式（1）進行方差分析，將數據的總變差中區分出試驗誤差和條件變差（試驗結果間的差異），并賦予它們的數量表示，即分解為各因素響應值之和、響應值均值和響應值的平方和（式（2））；各因素對應水平響應值的平方和均值（式（3））；各因素引起的離差平方和和總離差平方和（式（4））；試驗誤差（式（5）），以進行統計檢驗.

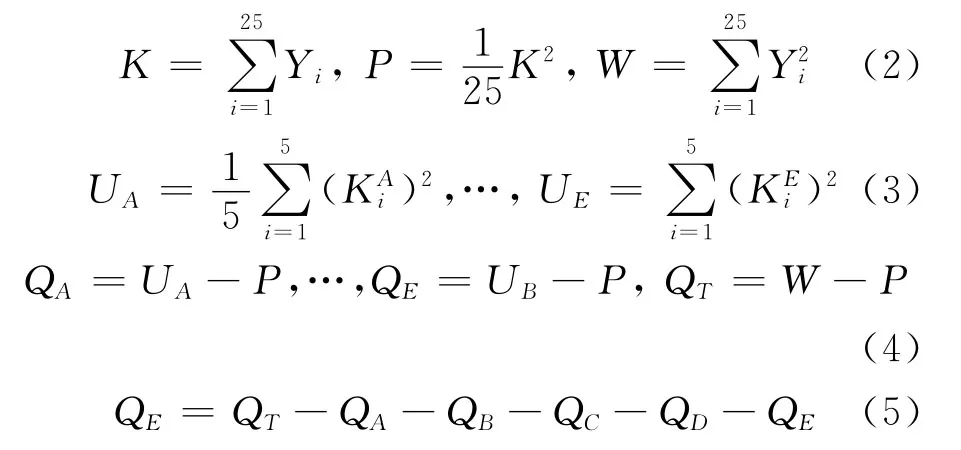
引入自由度的概念可消去數據個數的多少給平方和帶來的影響.總平方和自由度為n－1＝24，每個因子引起的離差平方和的自由度為4，而誤差自由度為n－1－r1（s－1）＝25－1－5（5－1）＝4，其中（r1≤r）.用各因素離差平方和除以相應自由度所得的商稱為均方離差.若式（1）的假設成立，均方離差的期望值相同，則有FA＝（QA／4）／（QE／4），等等.由此式來檢驗式（1）.即當式（1）假設成立時，F應服從F（s－1，n－1－r1（s－1））分布，從而小概率事件取在F值大的一側較為合理.

以0℃劈裂強度影響因素E為例分析.K＝（2.688＋2.669＋…2.65＋4.03）＝55.165，W＝（2.6882＋2.6992＋ … ＋2.652＋4.032）＝123.84，K1＝（2.688＋2.01＋2.366＋2.142＋2.65）＝11.856，K2＝（2.669＋2.042＋2.476＋1.618＋2.403）＝11.208，K3＝（2.325＋2.306＋2.192＋2.321＋1.86）＝11.004，K4＝（2.084＋2.281＋1.664＋2.423＋2.018）＝10.47，K5＝（1.737＋1.987＋2.27＋2.131＋2.502）＝10.627，＝140.565，＝125.619，＝121.088，＝109.62，＝112.93；UE＝（＋＋＋＋）＝609.826；P＝K2／25＝121.727，QE＝UE－P＝488.09；QT＝W－P＝2.115，誤差QE＝QT－QA－QB－QC－QD－QE.均方離差S＝QE／4＝0.059 7，F分布值＝S／QE＝3.969 2.給定顯著性水平α＝0.05，0.01，則F0.05（4，4）＝6.39，F0.01（4，4）＝15.98.從而0 ℃劈裂強度方差分析結果如表3。同理，15℃劈裂強度和45℃劈裂強度方差分析結果如表4.

表3 0℃劈裂強度方差分析結果

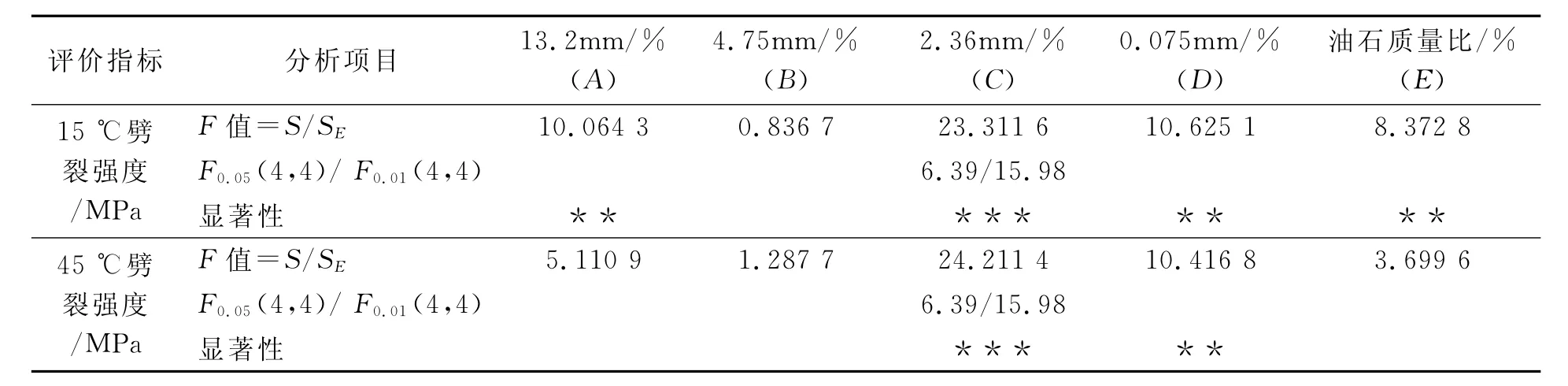
表4 15℃與45℃劈裂強度方差分析

2.2 極差分析

正交試驗設計方法的試驗因素均在變化，采用極差分析方法是判定因素影響主次的技術手段之一，極差是指各因素不同水平的試驗結果間的最大差值.設因素個數為N，序號為j＝1，2，…，N；每個因素水平數為M，水平序號為r，r＝1，2，…，M，同一水平只能作M次試驗.Ka為對應于各因素相應水平的不同溫度劈裂強度試驗結果，即評價指標；Kj為j因素N分別在同一r水平下Ka值之和的平均值，反應因素在該水平效應的大小.將同一因素各水平效應逐一進行比較，即可找出最佳和最差水平，從而求出極差：

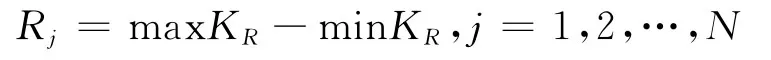
將各因素的極差進行比較，由極差大小順序可判定各因素的影響大小；通過各因素在不同水平的Kr值作因素水平與評價指標Ka之間的關系曲線，可得出各因素的影響程度和相應水平試驗結果的影響趨勢.不同溫度下劈裂強度極差分析結果見表5.

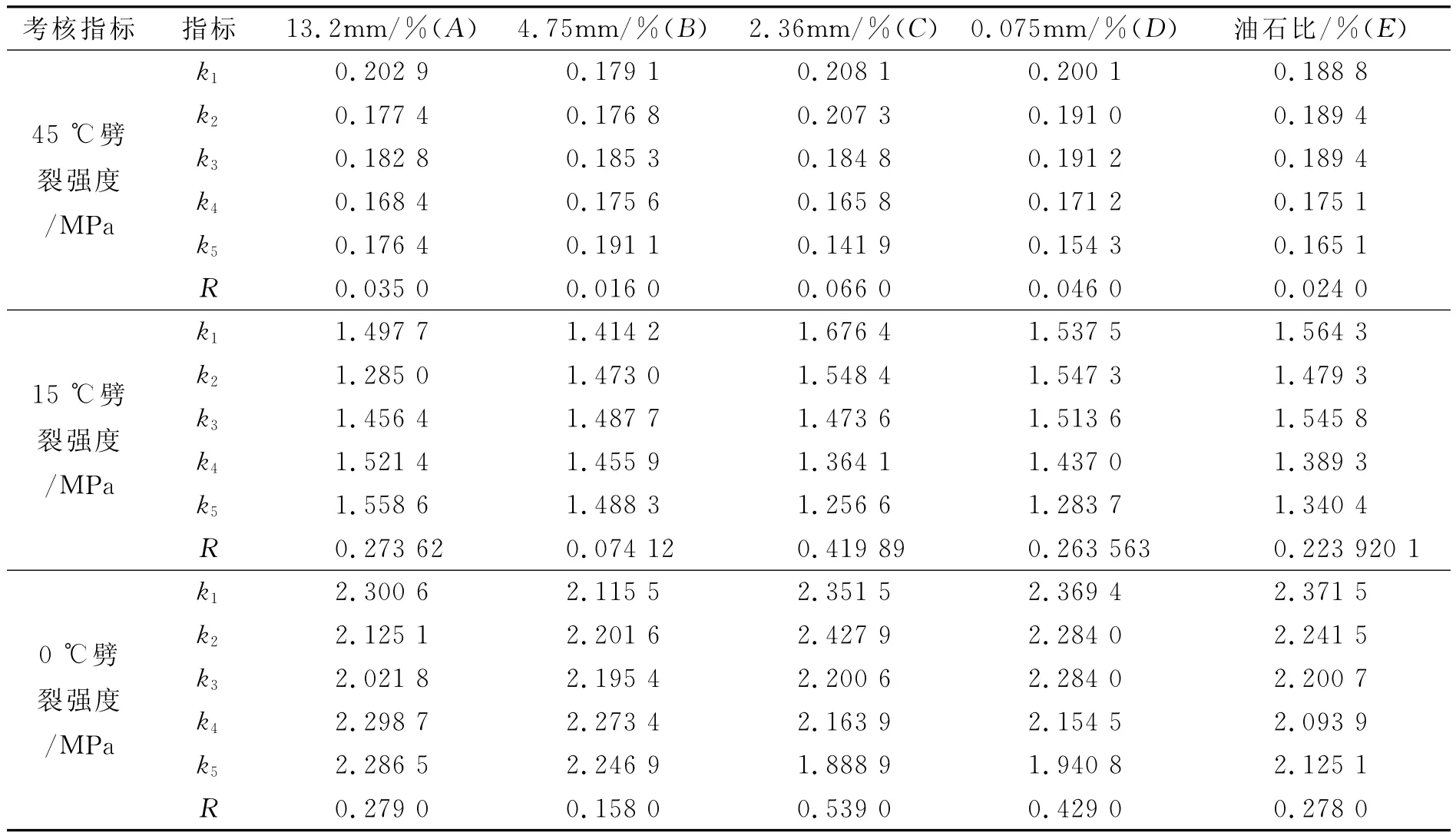
表5 不同溫度下融劈裂強度極差分析結果

1）由表3、表4可見，不同溫度下劈裂強度的影響因素大小排序均為C＞D＞A＞E＞B.其中，2.36mm通過率對不同溫度下的劈裂強度影響高度顯著，其次，0.075mm和13.2mm通過率的影響也較為顯著，而4.75mm通過率對不同溫度下的劈裂強度影響較小.試驗結果表明，不同溫度下AC－25瀝青混合料劈裂強度的影響因素程度并沒有隨試驗溫度的變化而發生排序上的改變，但影響程度有所差異.其中，2.36mm篩孔通過率是影響0，15和45℃劈裂強度最關鍵因素，且隨著溫度的逐漸升高，2.36mm篩孔通過率劈裂強度的影響愈加明顯，表明由壓應力轉化為拉應力受力模式下的劈裂強度隨溫度的逐漸升高，瀝青混合料的內部結構組成決定了抵抗劈剪的宏觀力學性能.

2）不同溫度劈裂強度并沒受到事先設計級配區間越大而表現出較大影響，如盡管2.36mm和0.075mm通過率變化較小，但對劈裂強度影響卻很大.說明礦料級配對不同溫度下劈裂強度起支配地位，尤其是細集料級配對其影響很大.

3）對比表5與表3、表4可知，不同溫度劈裂強度的各因素影響大小排序相同，表明作為直觀分析的極差分析，每個因素各水平對應試驗結果間的差異是因素水平變化所引起，并是試驗誤差所致，即來自12×25＝300個母體總體的試驗結果并不是試驗誤差造成.結合表5極差分析結果可知，當2.36mm通過率由12%增至28%時，0℃，15℃和45℃劈裂強度分別單調增加20%、25%和32%.

綜上所述，各因素所在列的差異實際上只反映該因子由于水平變動引起指標的波動，并不受到相鄰因子變動而改變，試驗結果證明了不同溫度劈裂強度值主要受控于礦料級配，優化級配不僅可提高路面高溫抗變形能力，也有助于提高中溫條件下瀝青路面的抗疲勞性能.

3 結 論

1）不同溫度下AC－25瀝青混合料劈裂強度影響因素的程度大小排序為2.36mm通過率＞0.075mm通過率＞13.2mm通過率＞油石質量比＞4.75mm通過率（C＞D＞A＞E＞B）；影響不同溫度劈裂強度的因素沒有隨溫度的變化而發生改變，只是其影響程度有所不同.隨溫度的逐漸升高，2.36mm篩孔通過率的影響越加顯著，說明優化2.36mm通過率可明顯提高路面的抗劈剪抗拉能力.

2）不同溫度下劈裂強度并沒有受到事先設計級配區間大小而發生較大變化，盡管考察因素4.75mm通過率變化24%，對劈裂強度影響并不明顯，而2.36和0.075mm通過率變化分別只有16%和6%，卻對劈裂強度影響顯著.當2.36mm通過率由12%增至28%時，不同溫度下劈裂強度分別單調增加20%，25%和32%.這與以前研究規律一致［8－9］.

3）方差與極差分析結果表明，2種數理統計分析結果是一致的，極差分析對因子（因素）作用的判斷并不是由于試驗誤差引起的，而是因子本身對實驗指標有顯著影響.表明正交試驗設計考核的各影響因素中，集料級配的變化對不同溫度下劈裂強度值的影響較油石比影響更大.

［1］魏建國，查旭東，鄭健龍，等.大粒徑瀝青混合料基層結構抗裂機理分析［J］.公路，2008，4：1－5.

［2］皮育暉，張久鵬，黃曉明，等.瀝青混合料劈裂試驗數值模擬［J］.公路交通科技，2007，24（8）：1－6.

［3］李曉軍，王貴榮，馮 樊.考慮非均勻性的瀝青混凝土間接拉伸強度測定儀研制與應用［J］.武漢理工大學學報：交通科學與工程版，2010，34（2）：310－313.

［4］李好新，索 智，王培銘.不同空隙率瀝青混合料的形變及破壞［J］.建筑材料學報，2008，11（3）：306－310.

［5］張 雷，陳靜云，喬英娟，等.間接拉伸試驗條件下瀝青混合料變形特性［J］.遼寧工程技術大學學報：自然科學版，2008，28（6）：856－858.

［6］彭 勇，孫立軍，石永久，等.瀝青混合料均勻性與材料力學性能關系，哈爾濱工業大學學報，2009，41（6）：142－145.

［7］中華人民共和國交通部.JTG F40－2004公路瀝青路面施工技術規范［S］.北京：人民交通出版社，2004.

［8］陸學元，張治鋒.AC－25瀝青混合料礦料級配優化與應用研究［J］.中外公路，2009，29（2）：207－213.

［9］陸學元，孫立軍.AC－13改性瀝青混合料劈裂強度的影響因素及其與馬歇爾性能指標的相關性［J］.吉林大學學報：工學版，2010，40（3）：666－682.