基于Gaussian－支持向量回歸機(jī)的高速公路短時(shí)交通量預(yù)測＊

趙澤輝 康海貴 李明偉 周鵬飛 莫仁杰

（大連理工大學(xué)工程建設(shè)學(xué)部1） 大連 116024） （河南省濟(jì)邵高速公路有限公司2） 濟(jì)源 454600）

高速公路迅猛發(fā)展，以交通控制與誘導(dǎo)系統(tǒng)為核心的智能交通系統(tǒng)ITS［1］應(yīng)運(yùn)而生，而實(shí)現(xiàn)ITS的關(guān)鍵問題是實(shí)時(shí)準(zhǔn)確的進(jìn)行交通量預(yù)測［2］，是進(jìn)行高速公路的路況分析、事件檢測及預(yù)測和預(yù)防交通擁堵的先決條件.因此，對(duì)高速公路短時(shí)交通量的準(zhǔn)確實(shí)時(shí)預(yù)測已成為高速公路智能化管理的一個(gè)重要環(huán)節(jié).在短時(shí)交通量預(yù)測方面，大致可以分為兩類：一類是基于確定數(shù)學(xué)模型的方法如時(shí)間序列預(yù)測模型和卡爾曼濾波模型等，另一類是基于知識(shí)的智能模型的預(yù)測方法如神經(jīng)網(wǎng)絡(luò)模型［3］、基于混沌理論的模型［4］等.支持向量回歸機(jī)（support vector regression，SVR）采用結(jié)構(gòu)風(fēng)險(xiǎn)最小化原則替代經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化原則，能根據(jù)有限的樣本信息，在模型的復(fù)雜性和學(xué)習(xí)能力之間尋求最佳折中［5］，克服了神經(jīng)網(wǎng)絡(luò)算法存在的全局搜索能力差或易收斂于局部最小等缺陷［6］，在解決實(shí)時(shí)性、波動(dòng)性和非線性問題中表現(xiàn)出許多特有的優(yōu)勢(shì)，應(yīng)用于短時(shí)交通量的預(yù)測取得了較好的效果［7－8］.本文利用遺傳算法（GA）進(jìn)行Gaussian－SVR模型參數(shù)的優(yōu)選，在預(yù)測過程中，綜合考慮了預(yù)測路段前幾個(gè)時(shí)段交通量、天氣因素和出行日期的影響，結(jié)合長濟(jì)高速公路某段西行方向的實(shí)測交通量進(jìn)行仿真預(yù)測，并進(jìn)行了對(duì)比分析.

1 基于Gaussian損失函數(shù)的支持向量回歸機(jī)

1.1 ε－損失函數(shù)支持向量回歸機(jī)

設(shè)已知訓(xùn)練集T＝｛（x1，y1），…，（xl，yl）｝.式中：xi∈Rd；yi∈R，i＝1，2，…，l，損失函數(shù)ε為：c（xi，yi，f（xi））＝｜yi－f（xi）｜ε，其 中：｜yi－f（xi）｜ε＝max｛0，｜yi－f（xi）｜－ε｝，此時(shí)基于ε－損失函數(shù)支持向量回歸機(jī)問題為：

式中：ω為d維列向量；C（C＞0）為懲罰系數(shù)；ζ（＊）＝（ζ1，ζ＊1，…，ζl，ζ＊l）為松弛變量.

引入Lagrange函數(shù)

式中：乘子a（＊），η（＊）≥0，為求它的極小，分別對(duì)ω，b和ζ（＊）計(jì)算偏導(dǎo)數(shù)，并同時(shí)引入核函數(shù)K（xi，yi），整理后得到問題（1）的對(duì)偶問題為

1.2 Gaussian損失函數(shù)的支持向量回歸機(jī)

設(shè)訓(xùn)練集T＝｛（x1，y1），…，（xl，yl）｝中的樣本點(diǎn)是由一個(gè)基本函數(shù)依賴關(guān)系ftrue和噪聲產(chǎn)生的，即

當(dāng)噪聲的密度函數(shù)p（ζi）已知，則在最大似然意義下，最優(yōu)的損失函數(shù)是

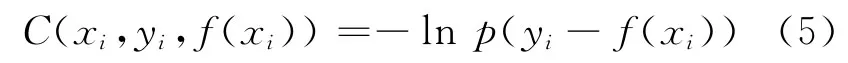
證明對(duì)式xf?｛（x1，y1），…，（xl，yl）｝的最大似然估計(jì)是

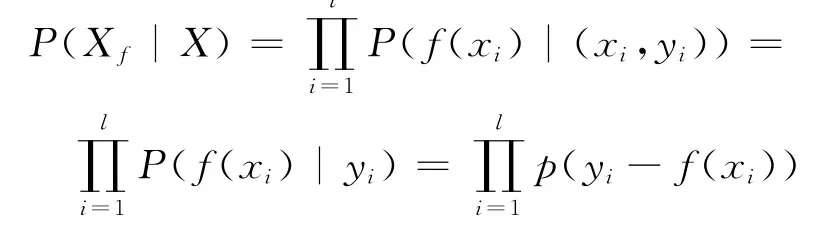
由式（5）和上式，得到

本文采用高斯函數(shù)進(jìn)行降噪處理，此時(shí)噪聲的密度函數(shù)為Gaussian函數(shù)，則有

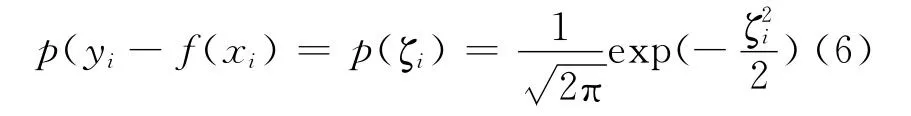
由式（5）知

此時(shí)，基于Gaussian損失函數(shù)的SVR為

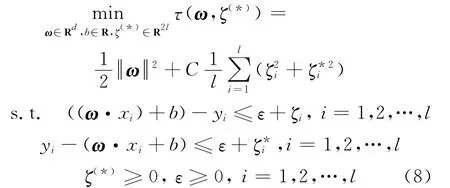
式中：ω為d維列向量；C（C＞0）為懲罰系數(shù)；ζ（＊）＝（ζ1，…，ζl）為松弛變量.

基于Gaussian損失函數(shù)的SVR模型算法步驟為

步驟1設(shè)已知訓(xùn)練集T＝｛（x1，y1），…，

步驟2選擇適當(dāng)正數(shù)ε和C，以及核函數(shù)K（xi，yi），本文核函數(shù)選為徑向基函數(shù).

步驟3構(gòu)造并求解最優(yōu)化問題

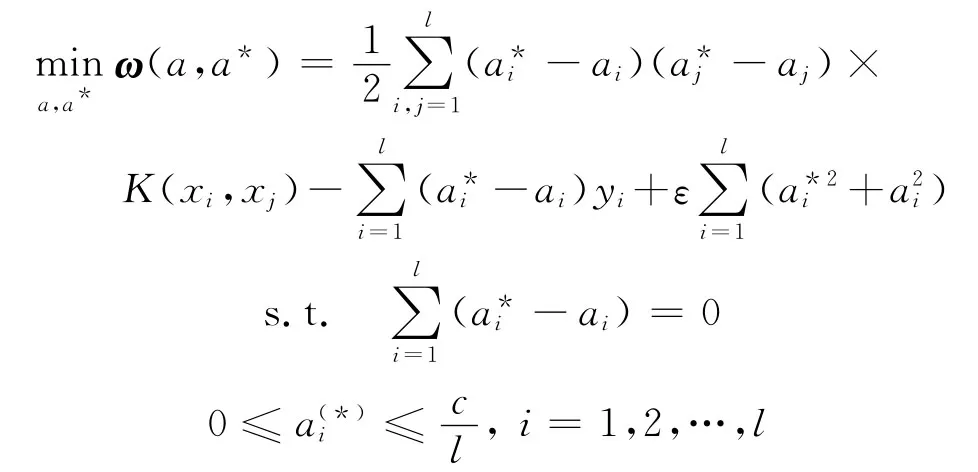
得到最優(yōu)解a（＊）＝（a1，…，ai；，…，）.

步驟4構(gòu)造決策函數(shù)

式中：按下式計(jì)算，選擇位于開區(qū)間（0，C／l）中的2個(gè)分量或，若選到的是，則

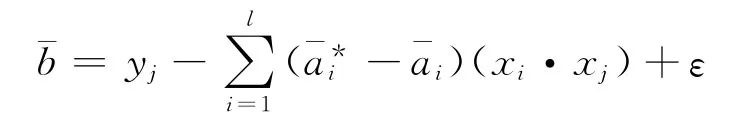
若選到的是，則

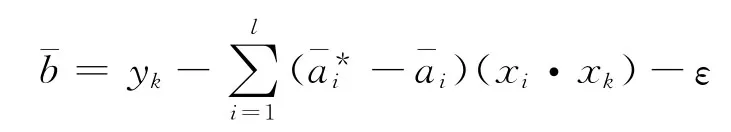
2 基于GA優(yōu)化的Gaussian－SVR短時(shí)交通量預(yù)測步驟

考慮到Gaussian－SVR參數(shù)的選取在一定程度上影響著模型的精度，本文應(yīng)用遺傳算法對(duì)Gaussian－SVR參數(shù)ε，C和δ2進(jìn)行優(yōu)選.

以訓(xùn)練結(jié)束后返回的回歸序列方差的倒數(shù)作為進(jìn)化個(gè)體的適應(yīng)值fitness

式中：n為輸入樣本個(gè)數(shù)；Y1（t）為回歸序列；Y（t）為實(shí)際序列值.GA－Gaussian－SVR預(yù)測模型的計(jì)算步驟如下.

步驟1歸一化處理.對(duì)實(shí)測量數(shù)據(jù)集和Gaussian－SVR參數(shù)的初始區(qū)間按式（12）進(jìn)行歸一化處理.

步驟2初始化父代群體.設(shè)種群規(guī)模為m，隨機(jī)生成父代群體y（j，i）（j＝1，2，3；i＝1，2，…，m），本文取m＝50，其中y（j，i）為第i個(gè)父代染色體上的第j個(gè)基因.

步驟3模型訓(xùn)練.以生成的每個(gè)染色體上的基因作為Gaussian－SVR參數(shù)，訓(xùn)練Gaussian－SVR模型，計(jì)算相應(yīng)的回歸序列，并根據(jù)回歸序列按式（11）計(jì)算染色體的適應(yīng)度值.

步驟4終止判斷.判斷當(dāng)前種群中最優(yōu)個(gè)體是否滿足終止準(zhǔn)則，若滿足轉(zhuǎn)入步驟7，否則轉(zhuǎn)入步驟5，進(jìn)化代數(shù)g＝g＋1.終止準(zhǔn)則采用最大進(jìn)化代數(shù)Gmax與相鄰進(jìn)化代數(shù)最優(yōu)個(gè)體適應(yīng)值相對(duì)誤差E相結(jié)合.

步驟5選擇、交叉和變異.根據(jù)步驟3計(jì)算所得的染色體的適應(yīng)度值，進(jìn)行選擇、交叉和變異操作.

步驟6生成子代新個(gè)體.由步驟5得到的3m個(gè)子代個(gè)體，按照其適應(yīng)值fitness從大到小進(jìn)行排序，取排在最前面的m個(gè)子代個(gè)體作為新的父代群體.轉(zhuǎn)入步驟3進(jìn)入下一輪演化過程.

步驟7模型預(yù)測.以當(dāng)前種群中最優(yōu)個(gè)體的染色體基因ε，和δ作為Gaussian－SVR參數(shù)訓(xùn)練模型，輸入待測樣本，輸出預(yù)測值.

計(jì)算流程見圖1.

3 實(shí)例預(yù)測與性能分析

3.1 高速公路交通量預(yù)測影響因素選擇

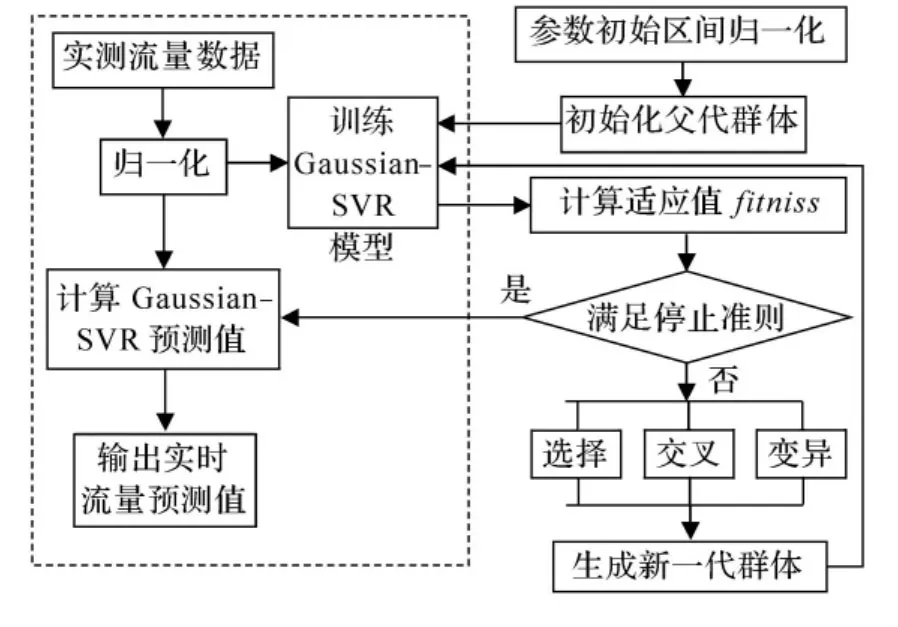
圖1 算法流程圖

交通流具有流體的特性，在時(shí)間上的分布是連續(xù)的，某路段下一時(shí)刻的交通量與本路段前幾個(gè)時(shí)段的交通量有著必然的聯(lián)系，所以可以利用本路段前幾個(gè)時(shí)段的交通量數(shù)據(jù)預(yù)測該路段下一時(shí)段的交通量，t表示交通量觀測的當(dāng)前時(shí)段，Y（t－3），Y（t－2），Y（t－1），Y（t）為預(yù)測路段前4個(gè)時(shí)段的交通量，Y（t＋1）為預(yù)測路段下一時(shí)段的交通量，因此，該路段t＋1時(shí)刻交通量Y（t＋1）的大小受交通量Y（t－3），Y（t－2），Y（t－1），Y（t）共同作用的影響.

考慮到高速公路通行在很大程度上受到天氣變化的影響，引入第五個(gè)輸入?yún)?shù)X1（t），X1（t）其量化方法為大雪或大雨雪為1，小雪或小雨雪為0.75，大雨為0.5，小雨為0.25，晴或多云為0.同時(shí)人們出行習(xí)慣也會(huì)對(duì)高速公路交通量產(chǎn)生影響，交通量以周為周期，在每周的不同天中，可能具有不同的變化規(guī)律，特別是在周末通行量會(huì)增多.因此，將出行日期作為模型的第六個(gè)輸入?yún)?shù)X2（t）.其量化方法為周一為1／7，周二為2／7，周三為3／7，周四為4／7，周五為5／7，周六為6／7，周日為7／7.至此，得到了影響預(yù)測路段下一時(shí)段交通量的6個(gè)影響因素X，作為模型的的輸入向量.

本文試驗(yàn)部分采用長濟(jì)高速公路濟(jì)源市內(nèi)某路段西行方向的交通量檢測儀于2009－06－01至2010－06－07一周內(nèi)獲取交通量數(shù)據(jù)，采集時(shí)段為10min，選取240組交通量數(shù)據(jù)并對(duì)其相應(yīng)的天氣和獲取日期進(jìn)行量化處理，組成模型訓(xùn)練樣本集，選取40組數(shù)據(jù)作為測試樣本集.

3.2 模型實(shí)例預(yù)測與性能分析

利用 Matlab 7.1編制 GA－Gaussian－SVR模型程序，運(yùn)行環(huán)境為：Core（TM）2CPU，1.81 MHz，2GB 內(nèi) 存 的 微 機(jī)，操 作 系 統(tǒng)：WindowsXP.模 型 初 始 值：C的 取 值 范 圍 為 ［1，2 000］，ε的取值范圍為［0，2 000］，δ的取值范圍為［0，20］，最大進(jìn)化代數(shù)Gmax＝1 000，鄰代最優(yōu)個(gè)體適應(yīng)值相對(duì)誤差E＝0.000 1.應(yīng)用本文提出的模型，經(jīng)過訓(xùn)練得到全局參數(shù)最優(yōu)組合為C＝213，ε＝41和δ＝0.23.將優(yōu)化后的模型用于測試樣本集的交通量預(yù)測.實(shí)際交通量與模型仿真輸出流量的對(duì)比圖和部分實(shí)際交通量與模型預(yù)測結(jié)果見圖2和表1，結(jié)果表明，預(yù)測結(jié)果曲線與實(shí)際交通量的變化曲線基本吻合，絕對(duì)誤差值基本控制在［－7，7］區(qū)間內(nèi)，只有少量超出這個(gè)范圍，預(yù)測結(jié)果達(dá)到了預(yù)期的預(yù)測效果.

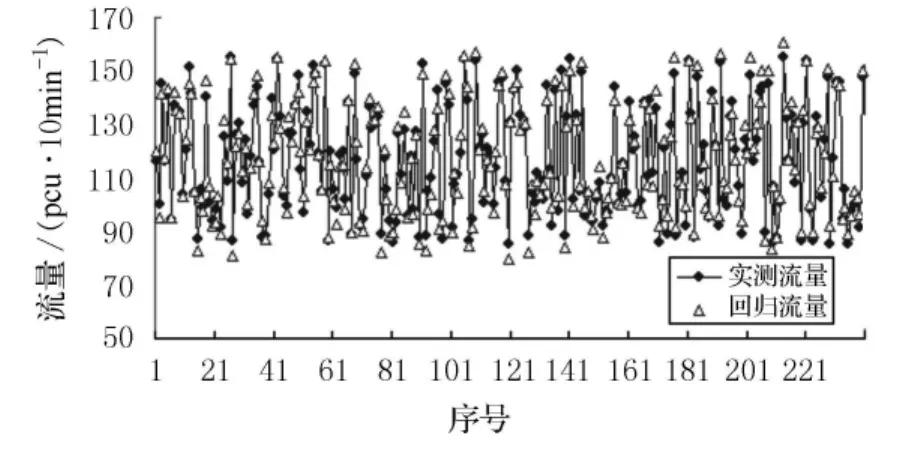
圖2 GA－Gaussian－SVR模型訓(xùn)練效果圖

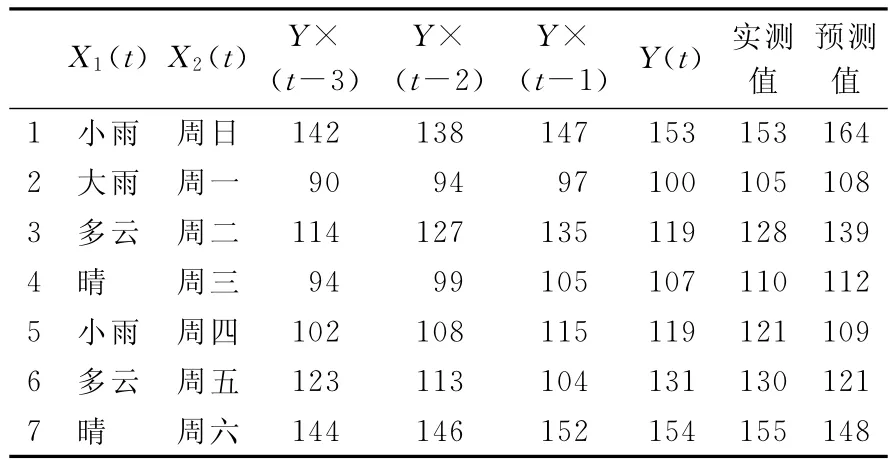
表1 部分實(shí)測流量與模型預(yù)測流量結(jié)果pcu／（10min）

為了比較GA－Gaussian－SVR模型的預(yù)測性能，本文選擇文獻(xiàn)［3］提出的PSO－BP神經(jīng)網(wǎng)絡(luò)模型、文獻(xiàn)［8］中提出的 WA－SVM預(yù)測模型和文獻(xiàn)［7］提出的G－SVR預(yù)測模型進(jìn)行對(duì)比分析.為了使對(duì)比模型具有可比性，4個(gè)模型均在同一臺(tái)微機(jī)上進(jìn)行計(jì)算，均使用matlab 7.1進(jìn)行編程.考慮到尋優(yōu)次數(shù)的增加也會(huì)提高優(yōu)化效果，對(duì)比模型參數(shù)的選取應(yīng)保證每個(gè)模型的最大尋優(yōu)次數(shù)相同，對(duì)PSO－BP神經(jīng)網(wǎng)絡(luò)模型優(yōu)選次數(shù)的設(shè)定，應(yīng)綜合考慮PSO算法和BP神經(jīng)網(wǎng)絡(luò)的尋優(yōu)次數(shù)，保證與GA算法具有相同的最大優(yōu)選次數(shù)，對(duì)WA－SVM預(yù)測模型參數(shù)的選擇，進(jìn)行多次交叉試算，盡可能的保證SVR參數(shù)的選擇精度.并采用以下3個(gè)評(píng)價(jià)指標(biāo)進(jìn)行性能對(duì)比分析

1）平均絕對(duì)相對(duì)誤差

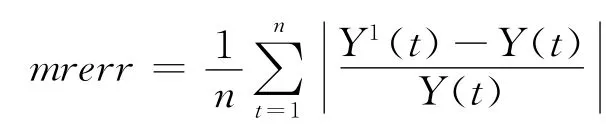
2）最大絕對(duì)相對(duì)誤差

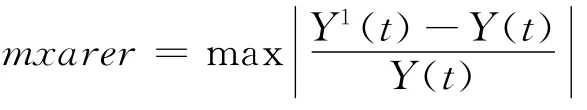
3）均方根誤差

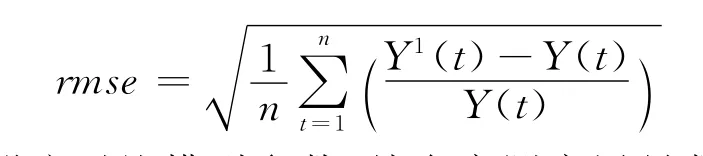
設(shè)定對(duì)比模型參數(shù)，結(jié)合實(shí)測交通量數(shù)據(jù)分別進(jìn)行模型訓(xùn)練，并對(duì)測試樣本進(jìn)行預(yù)測，將預(yù)測結(jié)果分別進(jìn)行誤差指標(biāo)處理，處理結(jié)果如表2所列.

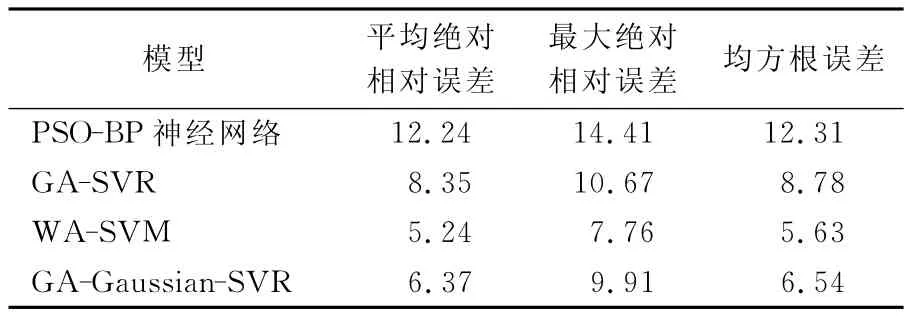
表2 預(yù)測誤差指標(biāo)比較 %

從表2中可以看出，在逼近原始流量序列的能力方面，SVM的預(yù)測方法明顯優(yōu)于PSO－BP神經(jīng)網(wǎng)絡(luò)模型.在對(duì)基于不同損失函數(shù)的SVM比較方面，采用高斯損失函數(shù)GA－Gaussian－SVR模型的誤差指標(biāo)值均優(yōu)于GA－SVR模型，說明在交通量序列中存在著成正態(tài)分布的噪聲，基于Gaussian損失函數(shù)的Gaussian－SVR模型對(duì)序列中的噪聲進(jìn)行了有效的處理，提高了模型的預(yù)測精度.在對(duì)噪聲處理比較方面，本文提出的模型的預(yù)測精度略低于 WA－SVM模型，但小波分析過程復(fù)雜，不利于ITS系統(tǒng)自動(dòng)操作，特別是對(duì)于實(shí)時(shí)交通量預(yù)測而言，在保證一定精度的范圍內(nèi)，操作的復(fù)雜程度和時(shí)間消耗更值得關(guān)注，從這個(gè)意義上講，本文提出的模型更適用于高速公路短時(shí)交通量預(yù)測.

4 結(jié)束語

從上述實(shí)例對(duì)比分析中可以看出：采用結(jié)構(gòu)風(fēng)險(xiǎn)最小化原則的SVR模型克服了神經(jīng)網(wǎng)絡(luò)模型存在的全局搜索能力差或易收斂于局部最小等缺陷，取得了較好的預(yù)測效果，Gaussian損失函數(shù)的引入彌補(bǔ)了SVR模型無法對(duì)序列內(nèi)噪聲進(jìn)行有效處理的不足，從而進(jìn)一步提高了模型的預(yù)測精度.針對(duì)運(yùn)行時(shí)間開銷主要取決于模型參數(shù)的尋優(yōu)階段，應(yīng)用GA進(jìn)行Gaussian－SVR模型參數(shù)的優(yōu)選，縮短模型尋優(yōu)階段的時(shí)間，提高尋優(yōu)效率，更適合于系統(tǒng)一定時(shí)段內(nèi)，利用新的數(shù)據(jù)進(jìn)行模型參數(shù)的自動(dòng)更新.在預(yù)測過程中，本文綜合考慮了長濟(jì)高速公路西行方向前四個(gè)時(shí)段的交通量、天氣和出行日期6個(gè)因素的影響，為對(duì)交通量進(jìn)行精確預(yù)測提供數(shù)據(jù)保障，實(shí)例分析過程中，實(shí)測流量與模型預(yù)測流量非常接近，達(dá)到了模型的預(yù)期效果，表明該模型適用于對(duì)高速公路短時(shí)交通流的預(yù)測.

［1］Mark D B.Peering into the future：peer－to－pee technology as a model for fistributed joint battlespace intelligence dissemination and operational tasking［D］.Maxwell Field，Alabama，USA：PhD＇s Thesis of School of Advanced Airpower Studies，Air University，2001.

［2］David P J.Rationality and self－interest in peer to peer networks［A］.Proceedings of the 2nd International Workshop on Peer－to－PeerSystems IPTPS＇03［C］／／Claremont Hotel， Berkeley， CA， USA：Springer press，2003.

［3］葉 嫣，呂智林.基于粒子群優(yōu)化的神經(jīng)網(wǎng)絡(luò)短時(shí)交通流量預(yù)測［J］.計(jì)算機(jī)工程與設(shè)計(jì)，2009，30（18）：4 296－4 299.

［4］郭 敏，藍(lán)金輝，肖 翔，等.基于混沌理論對(duì)北京二環(huán)路進(jìn)行短時(shí)交通流量預(yù)測的研究［J］.交通運(yùn)輸系統(tǒng)工程與信息，2010，10（2）：107－110.

［5］Vapnik V.The nature of statistical learning theory［M］.New York：Springer，1995.

［6］Cao J R，Cai A N.A robust shot transition detection method based on support vector machine in compressed domain［J］.Pattern Recognition Letters，2007，28（12）：1 534－1 540.

［7］任其亮，謝小淞，彭其淵.城市道路交通量短時(shí)預(yù)測的GSVMR模型［J］.公路交通科技，2008，2（52）：135－138.

［8］朱勝雪，周 君，包 旭.基于小波分解－支持向量機(jī)的短時(shí)交通量預(yù)測［J］.蘇州科技學(xué)院學(xué)報(bào)：工程技術(shù)版，2007，20（3）：80－85.