防護門結構模態分析

林家煒 張并瑞 石 磊

1 模型建立

根據某防護門設計尺寸，如圖1所示，門寬為4.3 m，高為3.0 m，門板厚15 cm。采用TrueGrid軟件建立有限元模型，該模型共有1 653 316個節點，1 499 036個單元，其中包含19 286個梁單元。

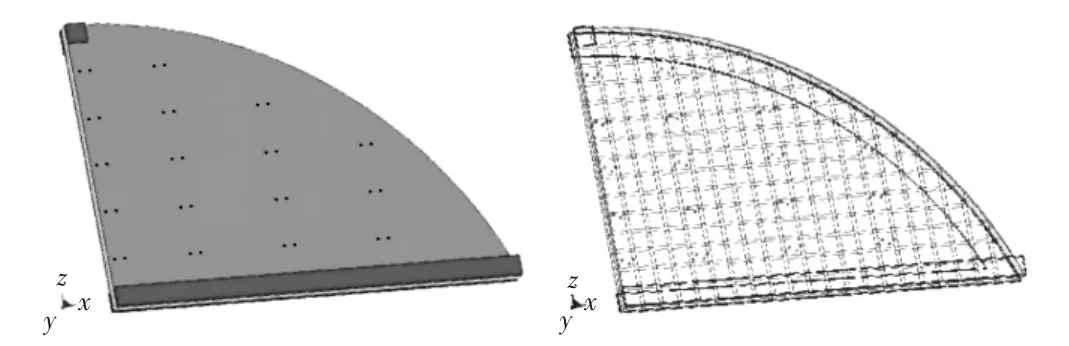
圖1 防護門結構示意圖與透視圖

結構的固有頻率和振型確定是進行等效靜載分析的基礎，也是編制結構荷載實用計算方法的前提。通過使用分塊位移求逆Lanczos方法對防護門進行模態分析，并研究防護門配筋對模態的影響。

2 模態分析的定義

模態分析是為了確定結構的振動特性，即結構的固有頻率與振型，它們是結構受動態載荷作用時的重要設計參數，并且也是其他動力學分析問題的基礎，如簡諧響應分析和譜分析、瞬態動力學分析。模態分析是進行這些動力學分析所必需的前期分析過程。

LS-DYNA解法中的分塊位移求逆蘭喬斯法，它來源于波音公司的數據庫(簡稱BCSLIB-EXT)。該解法采用共享內存的方法，它需求較大的內存，但計算速度快，并且能夠精確的提取大模型的多階模態(40階以上)。

其中，K，M分別為組合剛度與質量;Φ，Λ分別為固有振型的特征向量與特征值。

Lanczos運算法則通過迭代計算，得出的特征值和與之相對應的特征向量值越來越接近真實值。

其中，A為一實對稱矩陣，用于與特征向量相乘。當應用Lanczos運算法則計算振型分析問題時，式(2)應更改為:

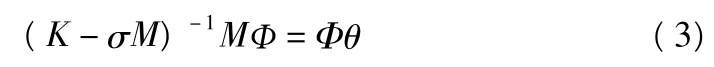
式(3)中每個分塊求逆特征值為θi=1/(λi－σ)。經過更改后能夠將復雜的問題轉變為普通特征值問題，這將大大提高蘭喬斯運算法則的計算速度。

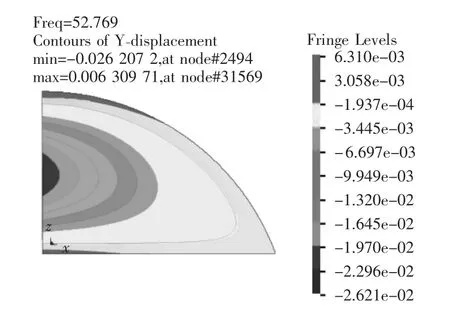
圖2 第1階振型圖