群樁基礎中土工參數相關范圍的分析
吳會閣王 麗,葛建龍
(1.石家莊經濟學院 工程學院,河北 石家莊 050031;2.河北省水資源可持續利用與開發重點實驗室,河北 石家莊050031;3.北京中鐵建筑工程設計院 天津分院,天津300011;4.天津振津工程集團有限公司,天津300222)
0 前言
在越來越多的高層建筑和高重構筑物設施中,群樁基礎以其承載力高、沉降小、生命力強等特點得到了廣泛的應用。巖土工程參數的正確選取是群樁基礎可靠性的重要保證,在各參數中土的物理性質和力學性質的空間變異性最大,描述這種空間變異性較好的方法是文獻[1]提出的土工剖面的隨機場理論,而反映土工參數空間變異特性的重要指標是土層的相關范圍。近年來,國內外一些學者對土工參數的相關范圍進行了一系列研究,文獻[2]用一維平穩高斯隨機場理論,研究了用回歸模擬方法計算土工參數的相關范圍;文獻[3]用改進的空間遞推平均法討論了土工參數相關范圍的確定;文獻[4]用非線性曲線擬合法計算了土性的相關范圍;文獻[5]用相關函數法討論了相關范圍確定中相關函數的選取及擬合區間;文獻[6]對目前確定土工參數相關范圍的幾種方法進行了評述,指出空間遞推平均法雖計算方便,但平穩點難以確定,其計算結果受人為因素影響較大,曲線擬合法算出的相關距離值偏小。
在對群樁基礎的可靠度分析時,本文擬采用相關函數法和變異函數法計算土工參數的相關范圍。
1 土工參數的空間變異性
在天然土層中,土性指標在各點是確定的,根本不存在隨機性的問題,“唯一”不確定的問題是無法知道土工參數在土層中每一點的取值[7]。
土工參數的空間變異由以下3部分組成:

其中,E[X(Z)]為土工參數的趨勢分量,是非隨機的變量,可由最小二乘法回歸;X'(Z)為零均值,方差為σ2的正態分布隨機變量,{X'(Z)}為一平穩隨機場,代表土性固有變異性;ε(Z)為測量誤差。
對于平穩的隨機場,其統計特征不隨位置的不同而不同,其均值、方差以及自相關函數都可以通過樣本相應的平均(隨機過程的時間平均)得到。對于有連續變化的X'(Z)而言,由Shannon抽樣定理,這時要求采樣能再現原來連續曲線中含有的全部信息,從這一角度出發,取樣間距越小、采樣點越多越好;但取樣間距太小,會增加點均值的統計誤差、低估點的變異性。當取樣間距小于相關范圍時,由于土性自相關性的影響,用傳統的獨立、同分布序列統計方法計算“點”均值、“點”方差以及自協方差函數的無偏估計時,要加以修正。
2 兩種算法的基本原理
2.1 相關函數法
2.1.1 相關函數理論[8-10]
對于一均質土層某一點t的土性記作x(t),則x(t)的概率特性可表示為:

那么,土層中任意兩點t,t+h之間的相關函數可用下式表示:

式中Γ2(h)為方差折減系數。
常用的理論相關函數有三角型、指數型、指數余弦型等,其對應的函數形式和相關范圍(或變程)計算公式見表1。

表1 理論相關函數模型
2.1.2 相關范圍的確定
用相關函數確定相關范圍,就是用一定類型的理論相關函數模型去擬合實測相關函數曲線,求出相應參數,代入對應的相關范圍計算公式求得結果。
相關函數法求解相關范圍的步驟:
(1)原始數據的處理:將試驗測得的原始數據X0i標準化后作為樣本值Xi,即:
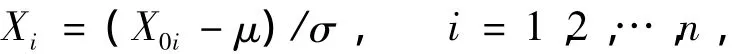
式中,μ,σ分別為原始數據的均值和標準差。處理后,樣本均值為0,方差為1。
(2)取間距τ1=△Z,△Z為取樣間距,計算相關函數值:

(3)分別取間距 τ2=2τ1,τ3=3τ1,…,τm=mτ1,…(m < n),分別計算出此時的相關函數值:

(4)此時,所得到的相關函數為實測的相關函數,可做出實測相關函數曲線,根據實測相關函數曲線選擇合適的理論相關函數模型,對實測曲線進行擬合,把擬合出的相應參數代入計算公式即可。
2.2 變異函數法
2.2.1 變異函數理論
土的空隙度、相對密度、塑性指標、滲透系數、壓縮模量、抗剪(壓)強度以及某一特定持力土層的厚度都可看作是區域化變量。區域化變量一般可反映巖土參數的尺寸效應,不同程度的連續性和不同種類的異向性及空間變化的可遷性等特征。
對于一個代表巖土參數的區域化變量Z(x),變異函數可定義為向量h相隔的Z(x)、Z(x+h)兩個區域化變量間增量平方的數學期望的一半,或兩區域化變量增量的方差的一半(也稱半變異函數),本文仍稱之為變異函數:
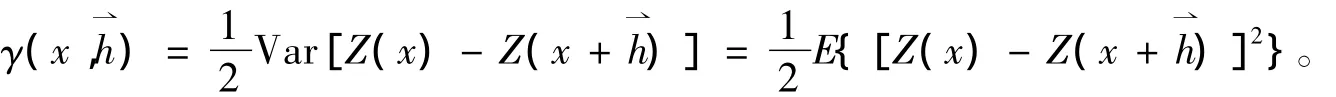
由上式可知:變異函數是點x和向量h兩者的函數。由于在任意點上不可能獲得一系列樣本值,因此要求Z(x)滿足本征假設條件,即可認為[Z(x)-Z(x+h)]只依賴于h,而不依賴于x,則可用實際觀測值計算變異函數的估計量,即:

式中,N(h)是以向量h相隔的試驗數據對Z(xi)和Z(xi+h)的數目。
常用的理論變異函數模型有球狀模型、指數模型、高斯(Gauss)模型等,其中最常用的是球狀模型。各種模型的函數形式及其對應的相關范圍(或變程)值見表2和圖1。

表2 理論半變異函數類型
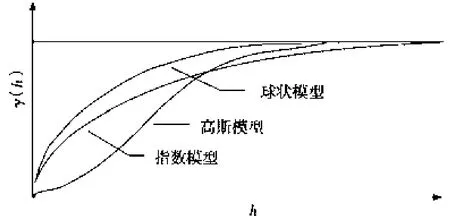
圖1 理論變異函數模型
2.2.2 相關范圍的確定
與相關函數法相似,變異函數法是用理論變異函數去擬合實測變異函數曲線,從而得出相應的參數,代入公式求得相關范圍的值。
變異函數法求解相關范圍的步驟:
(1)試驗測得的原始數據作為樣本值{X(t)},這時,樣本均值為 μ,方差為 σ2。
(2)△Z為取樣間距,取間距τ1=△Z,計算這時的變異函數值:
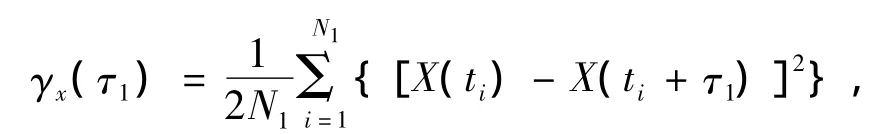
其中N1表示相距τ1的樣本點對數。

(4)此時,所得到的變異函數為實測變異函數,可做出實測變異函數曲線,根據實測變異函數曲線形式選擇合適的理論變異函數模型對實測曲線進行擬合,求出參數后,便得到相關范圍(或變程)值。
3 工程計算實例
圖2為實測的天津地區某臨近場地的靜力觸探曲線,fs為雙橋探頭測得的側摩阻,kPa;qc為作用于探頭上的阻力,MPa;h為相關范圍,m。
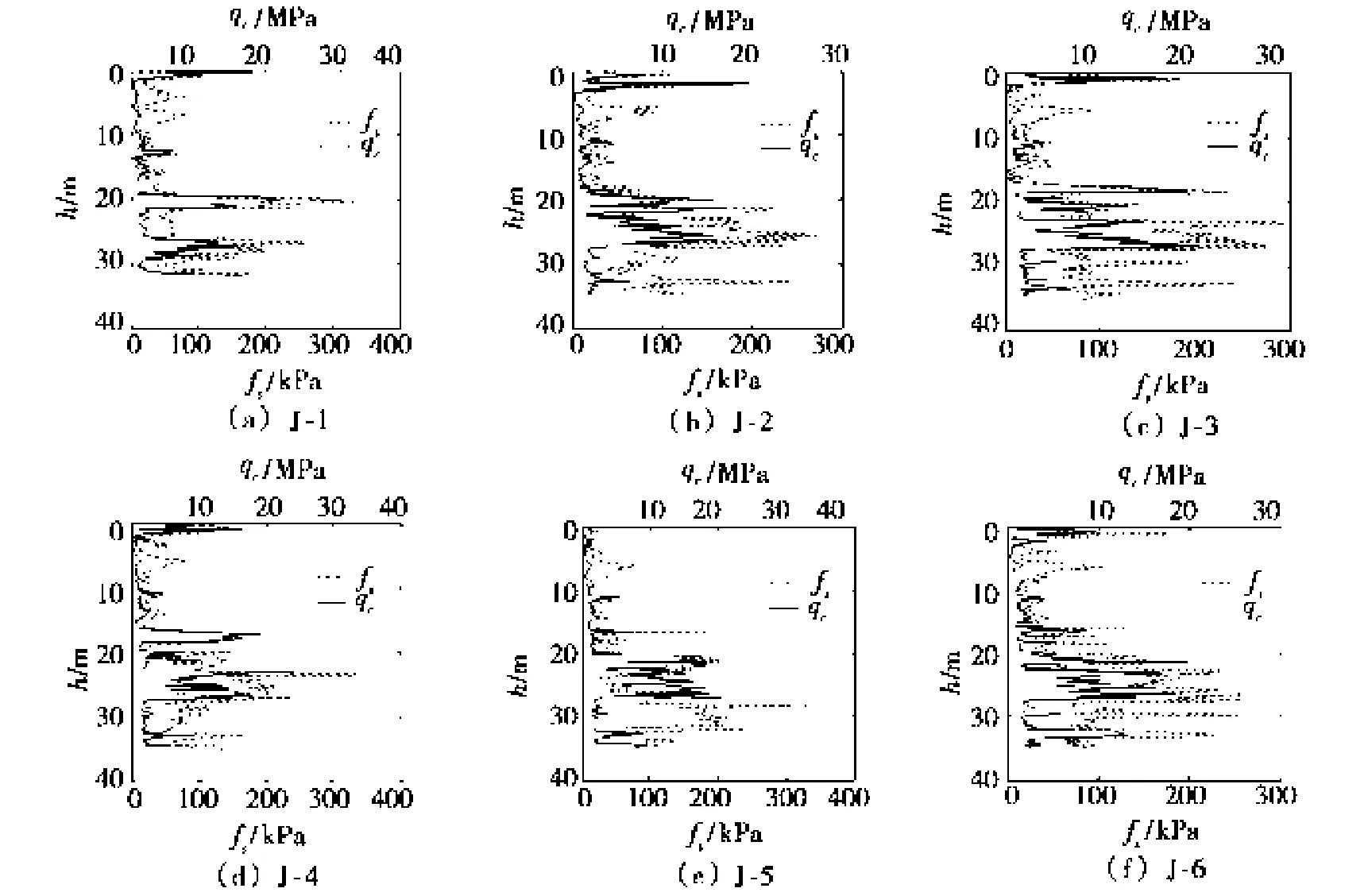
圖2 試樁靜力觸探曲線
基于指數模型,對各孔土層的相關范圍分別采用相關函數法和變異函數法進行了計算。以J-5孔為例,具體計算結果如表3所示,考慮到計算結果的用途,本文只計算到樁端持力層,且計算結果為各土層側阻的相關范圍,對于端阻的相關范圍,只考慮了樁端持力層。由表3可見:兩種方法計算出的絕大多數土層的相關范圍很接近,說明在對群樁基礎的可靠性分析時,利用相關函數法和變異函數法均具有一定的可靠性,計算結果精度較高;少數結果有一定差距,為了降低計算結果的誤差,推薦采用兩種算法的平均結果。其余各孔的計算結果如表4所示,該結果為兩種計算方法的平均值。

表3 J-5孔土層的相關范圍

表4 各孔土層的相關范圍
4 結論
(1)在鉆孔灌注群樁基礎的可靠度分析中,隨機場理論是考慮土工參數空間變異性的重要方法。
(2)采用相關函數法和變異函數法對群樁基礎中的相關范圍進行研究,通過比較發現兩種算法都具有較高可靠性。
(3)采用相關函數法和變異函數法計算結果的平均值,作為各土層的相關范圍,可進一步減小如人為因素等原因引起的誤差。
[1]Vanmarcke E H.Probabilistic Modeling of Soil Profiles[J].Journal of the Geotechnical Engineering Division,ASCE,1977,103(11):1227-1246.
[2]傅旭東.土工參數相關范圍及相關距離的計算方法[J].西南交通大學學報,1996,31(5):510-515.
[3]張梅,丁繼輝,宋向東.對求解土性相關距離的空間遞推平均法的分析與改進[J].河北農業大學學報,1999,22(1):85-89.
[4]丁繼輝,宇云飛,張慶宏,等.土性相關距離計算的非線性曲線擬合法[J].勘察科學技術,2000(3):13-16.
[5]程強,羅書學,高新強.相關函數法計算相關距離的分析探討[J].巖石力學,2000,21(3):281-283.
[6]劉春原.基于GIS系統的巖土參數隨機場特性研究[D].天津:天津大學,2003.
[7]姚若軍.土性參數空間變異和相關情況下的土坡可靠度分析[D].武漢:武漢大學,2005.
[8]郭懷志,彭大鵬.材料性能的隨機場特性參數的檢定方法[J].巖土工程學報,1994,16(3):21-29.
[9]宋向東,任建華.土工參數隨機場模型中相關函數的選擇[J].數理統計與管理,2007,26(5):773-775.
[10]尹利華,王曉謀,張留俊.天津軟土土性指標概率分布統計分析[J].巖石力學,2010,31(2):462-468.

