基于小波變換的遙感圖像壓縮①

郭廣杰，張 靜，郭海生

（1.河南省舞鋼市建設局，河南 舞鋼462500；2.信息工程大學測繪學院，河南 鄭州450052；3.河南省靈寶市國土資源局，河南 靈寶472501）

0 引 言

遙感數據的大信息量、大容量和越來越高的分辨率對圖像的存儲和傳輸提出了更高的要求，因此有效的圖像壓縮就顯得特別重要。小波變換是發展起來的可以對信號進行多尺度分析的工具，由于其具有良好的時頻局部化特性，在圖像處理領域也得到了廣泛的應用，尤其在圖像壓縮編碼方面取得了比較好的效果。小波基也有無窮多組，用不同的小波基函數對信號進行小波變換和壓縮編碼，得到的結果是不同的。當然并不是所有的小波基適合于圖像的壓縮編碼，這就要求根據不同小波基性質與圖像壓縮編碼特點的對應關系，有針對性的選擇適合的小波基進行圖像壓縮。

而小波基的選擇又直接決定了圖像壓縮的壓縮效果和壓縮速度。

1 小波變換基礎

小波函數的定義［1－2]為：設φ（t）為一平方可積函數，即φ（t）∈L2（R），若其傅立葉變換Ψ（w）滿足條件

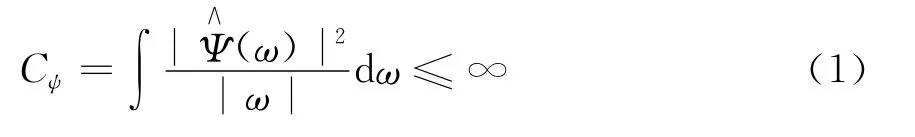
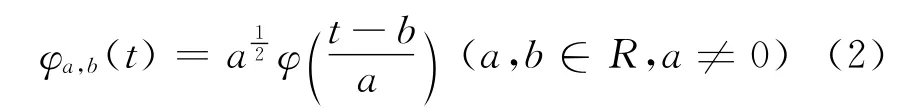
稱φa，b（t）為依賴于參數a，b的小波基函數，式中：a為伸縮因子或尺度因子，將基本小波伸縮；b為平移因子，將基本小波作位移。

對于任意的函數或者信號f（t）∈L2（R），用小波函數集 ｛φa，b（t）｝進行分解運算，其連續小波變換為

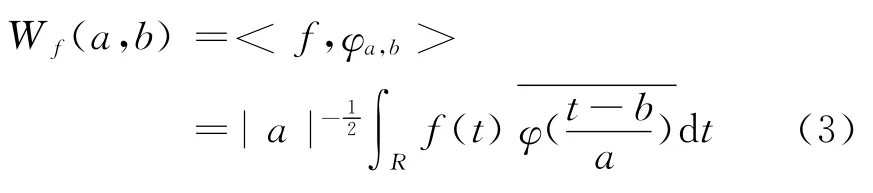
已經證明，如果采用的小波滿足可容性條件式（1），則其逆變換存在，即根據信號的小波變換系數可以精確地恢復原始信號，其逆變換（重構）公式為

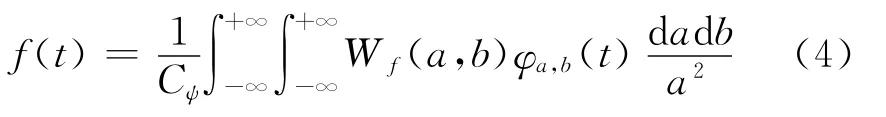
而圖像是二維信號，因此，需將小波……