12C18O和13C16O分子X1∑+基態的完全振動能譜和同位素位移

劉杰超,馬永健,竇 亮

(深圳大學 物理科學與技術學院,廣東深圳 518060)

紅細胞壽命縮短是導致貧血的原因之一,但是造成紅細胞壽命縮短的原因比較復雜,目前尚未完全清楚。如果能即時判斷紅細胞壽命是否縮短,為臨床即早進行治療,緩解病情提供幫助。研究[1]證實,用呼氣中CO濃度可判斷紅細胞壽命是否縮短。故利用穩定同位素標記的一氧化碳12C18O和13C16O進行呼氣試驗,可準確探測呼氣中CO的濃度。測量穩定同位素的傳統方法是質譜法,但質譜儀費用昂貴,操作復雜。如果能詳細了解同位素標記的分子12C18O和13C16O相對于12C16O的光譜移動(即同位素位移),則可能建立一種通過測光譜來測定12C18O和13C16O的方法,大幅減化操作過程,減少費用。12C16O分子X1∑+基態的實驗振動光譜已有文獻[2]報道,但12C18O和13C16O的振動能譜卻未見相關報道。

對于CO這樣的多電子雙原子分子體系,常用的研究能譜量子力學變分理論從頭計算法(Abinitio)比較復雜[3],而且大多數使用單電子軌道近似、固定核近似(Born-Oppenheimer近似)[4-6]等物理模型。在這些模型中,多次使用變分參數,致使計算結果的精確性受到很大影響。本工作擬根據實驗已經獲得的12C16O分子X1∑+基態精確的低振動能譜,結合代數方法(Algebraic Method,AM)和Herzberg的同位素效應理論,計算12C16O分子X1∑+基態的完全振動能譜和同位素分子12C18O和13C16O的各項光譜常數,比較12C18O和13C16O與12C16O同級能級之間的同位素位移,為相關研究提供參考。

1 理論與方法

1.1 AM方法理論

對于多電子體系,精確的量子力學計算非常復雜。利用這種繁雜的方式得到非常精確可靠的能譜是很困難的。雖然實驗上已經積累了很多分子電子態的部分振動能級光譜數據,但對于大多數分子電子態來說,其完全振動能譜的實驗光譜數據還非常缺乏。如何用已知實驗數據得到目前實驗上尚未得到,且其他理論也難以得到的精確可靠的分子電子體系的完全振動能譜{Eυ},是件很值得研究的事情。

AM的基本思想如下。1)由于將振動本征能量同本征量子態聯系在一起的解析關系式是振動能級公式,對于分子電子態的全程振動范圍而言,都可以通過能級表達式將本征能量同振動光譜常數集合與本征量子態解析地正確聯系在一起。2)對于給定分子電子態而言,已知的部分振動能級的各種組合都將分別構成其完全振動能譜集合{Eυ}的一個能級子集合[Eυ],而任一子集合中的每一個振動能級都完全滿足解析振動能級表達式。3)如光譜實驗或嚴格的量子力學計算足夠精確,則完全振動能譜的一切振動信息就包含在已知的子集合[Eυ]中。但在很多情況下,對于給定的分子電子態而言,由于實驗方法或量子力學處理所產生的很難避免的誤差,而導致測得的某些實驗數據或算得的某些振動能級也帶有誤差。所以,并非所有的子集合中的每一個振動能級Eυ所對應的振動光譜常數集合都具有相同的精確度。因此有必要建立一定的物理方法并尋找一定的物理判據,從一組己知的振動能級中將能夠正確代表該電子態的真實振動光譜常數集合遴選出來。4)利用遴選出來的正確振動光譜常數集合代入表征完全振動能譜的能級表達式求得該分子電子態的完全振動能譜{Eυ}的精確數據。

以上即是AM方法研究雙原子分子體系電子態的完全振動能譜{Eυ}所依據的基本思想。其核心在于所建立方法的嚴格性和如何選擇能夠代表完全振動能譜的正確能級子集合[Eυ]。

1.2 方法

在分子的電子態確定后,理論上該電子態的分子振轉能量可以通過求解原子核運動的Schr?dinger方程得到。哈密頓量中勢能函數不同,可以得到不同近似程度的振轉能量及其表達式。雙原子分子常用的勢能函數有簡諧振子函數(SHO)[7]、Morse函數[8]、HMS勢能函數[9]和Murrell-Sorbie勢能函數[10-12]等。構造這些經驗勢能函數要用到一些實驗參數,所以勢能函數本身的精確度受到這些實驗數據精度的影響。雙原子分子體系核運動的非相對論徑向Schr?dinger方程表達式如下:

(1)式中,h為普朗克常數;μ為雙原子體系的折合質量;R為核間距;V為雙原子分子的核運動勢能;J為轉動量子數;Λ是體系電子的總角動量L在Z軸分量的本征值;Ψ為雙原子體系電子的波函數;E為振轉能量的本征值;υ為振動量子數。求解這個微分方程,可以得到雙原子分子的振轉能級。利用Sun等[13-14]建立的以非諧振子模型為基礎并結合量子力學的二階微擾理論,得到雙原子分子的振轉能量表達式如下:

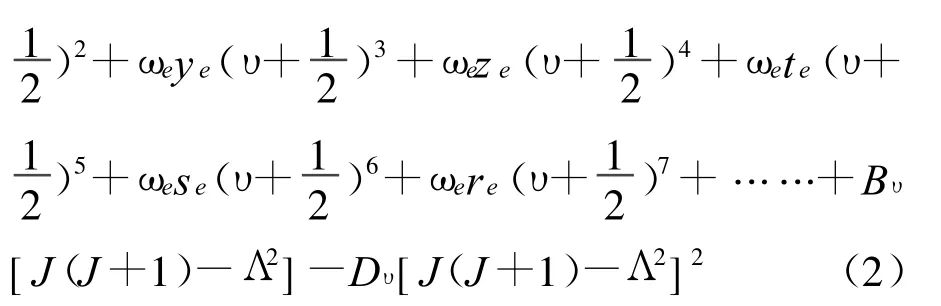
(2)式中,ω0、ωe+ωe0、-ωexe、ωeye、ωeze、ωete、ωese和 ωere為非諧性振動常數 ;ωe0是對諧性振動常數ωe的修正項;υ為振動量子數;Bυ為振動態υ中的轉動常數;Dυ為振動態υ中表示離心力影響的平均轉動常數。對于確定的雙原子分子電子態,振動能量遠遠大于轉動能量[7],因此在忽略轉動能級貢獻的情況下,非相對論核運動振動能譜的解析表達式為:

(3)式中,ω0和 ωe0是微小量,它們在計算高階振轉能級時有不可忽略的貢獻。用AM方法計算振動光譜常數和完全振動能譜的基本出發點是將正確的微擾振動能級解析式(3)式寫成矩陣形式[13]:

其中振動光譜常數的向量矩陣X和振動能量矩陣E分別表示為:

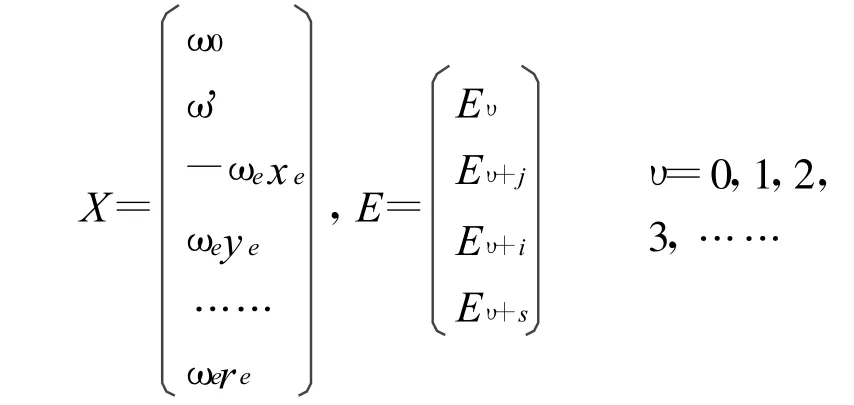
上式中,ωe'=ωe+ωe0,A為含有n×8個矩陣元的系數矩陣,其矩陣元的形式為Aυk=(υ+)k,k=0,1,2,3,4,5,6,7。對于一個雙原子分子確定的電子態,若已知M(M≥8)條低振動能級[Eυ],便可從中選出8條振動能級作為已知振動能級許多子集合中的一個來構成振動能量矩陣E,進而通過代數方法,得到一組振動光譜常數[ω0,ωe',-ωexe,ωeye,ωeze,ωete,ωese,ωere] 。將其帶入(3)式中,即得到體系的一組完全振動能譜Eυ。而根據振動能譜的物理性質,一套能夠表示一個確定電子態的完全振動能譜的光譜常數應滿足以下性質[13-14]:

(5)～(9)式是挑選代表體系完全振動能譜Eυ的最佳物理表象的判據條件。(5)式和(8)式表示最高振動能級的收斂極限,對于分子長程無能壘的情況,De對應體系的兩原子相距無窮遠時的平衡離解能;(6)式和(7)式表示在離解極限處相鄰能級所要滿足的物理條件;(9)式表示AM能級和實驗能級要高度吻合。由此可從部分已知的精確低振動能級[Eυ]中找到滿足判據條件(5)～(9)式的實驗振動能級的最佳子集合,從而獲得一組能夠代表體系真實振動信息的精確振動光譜常數及該電子態的正確的完全振動能譜Eυ。這就是獲得雙原子分子電子態的精確振動光譜常數和完全振動能譜的AM方法。

2 結果與討論

2.1 AM方法確定的12C16O分子X1∑+基態的完全振動能譜

根據實驗測出的12C16O分子X1∑+基態的低振動能譜(υ=0～37)[2],即可選能級數目 Μ=38。將AM方法得出的完全振動能譜和由文獻[2]提供的低振動能譜列于表1。

由表1可以看出,AM方法計算出的完全振動能譜在低能級時與實驗值吻合,滿足判據條件(9)式,說明該方法在計算雙原子分子振動能譜中的可靠性。已知12C16O分子X1∑+基態的離解極限為De=90 544.760 0 cm-1[2,15]。當振動量子數υmax=77時,用AM方法得出的振動能級E=90 542.734 4 cm-1,已經很接近其離解極限,相對誤差僅為2.237×10-5。當時υ=78,E=90 496.799 0 cm-1,已經出現收斂跡象 ,Eυmax-Eυmax-1=3.707 4 cm-1,已經足夠小,滿足判據條件(5)～(9)式。計算結果表明,在實驗振動能譜Eυexp的精確性可靠的情況下,用AM方法得出了相當精準的12C16O分子X1∑+基態的完全振動能譜。

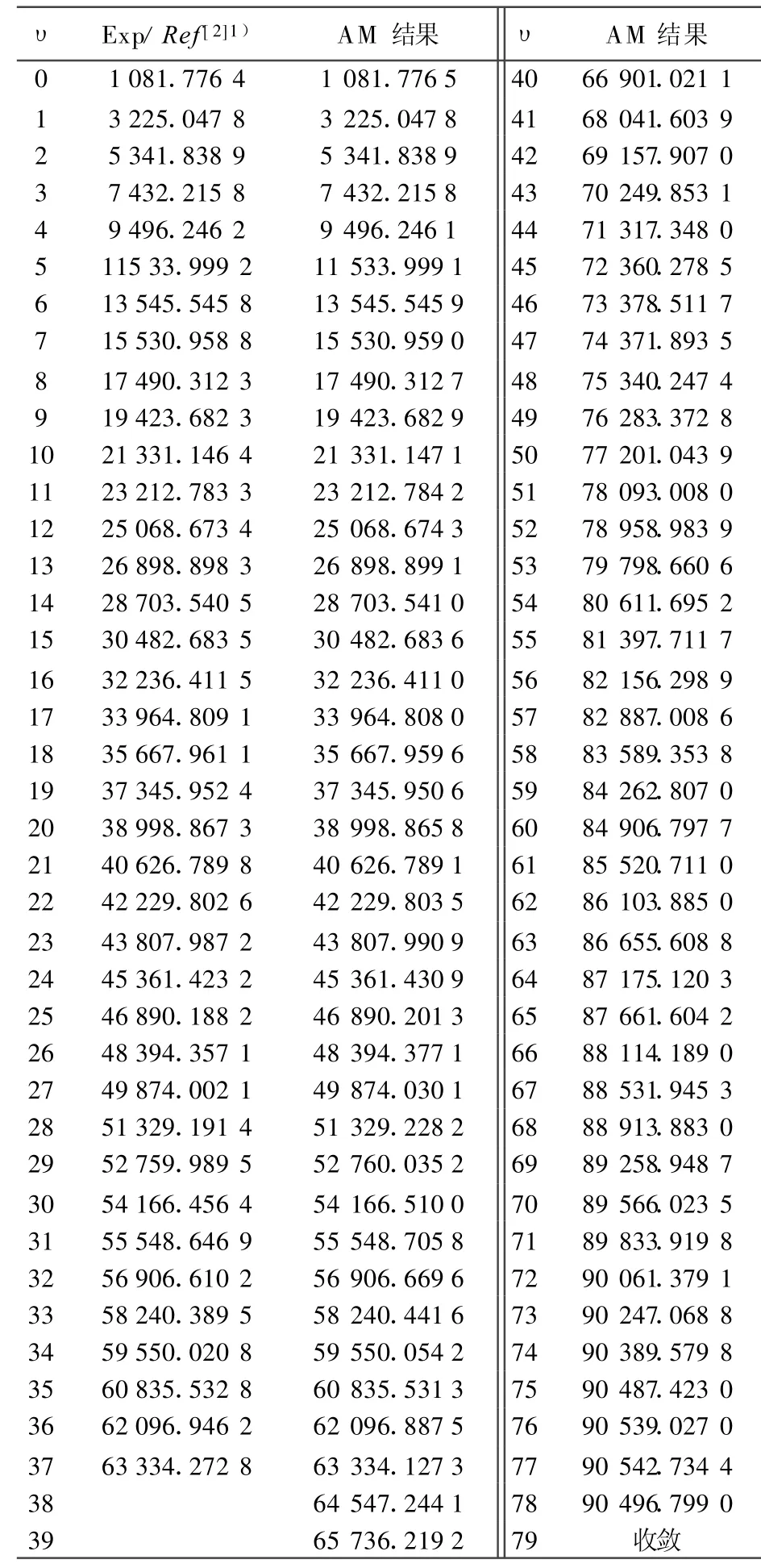
表1 12C16O分子X1∑+基態振動能譜的AM計算結果與實驗結果的比較 cm-1

2.2 12C18O和13C16O光譜常數和振動能級的同位素效應

根據Herzberg的同位素效應理論[7],由同位素分子的折合質量之比,可以確定一個同位素參數ρ,通過該參數可以將同位素分子的相關光譜常數聯系起來。

(10)～(13)式中,μ為CO分子的折合質量,其上標i為同位素分子。根據(10)～(13)式,利用AM方法得出的12C16O的振動光譜常數,計算出了同位素分子12C18O和13C16O的光譜常數,并得出它們的振動能譜。12C16O、12C18O和13C16O的光譜常數和同位素位移列于表2和表3。

3 結 論

對于12C16O分子X1∑+基態[16],根據實驗測出的部分精確的低振動能級,就可以用AM方法求得該電子態的完全振動能譜Eυ。這在一定程度上彌補了實驗方法不能測出高振動激發態能級的缺陷。本工作采用AM方法計算出12C16O的光譜常數,并結合Herzberg的同位素效應理論,確定了12C18O 和13C16O分子 X1∑+基態的振動光譜常數,進而計算出了它們的振動能譜。由計算結果可以看出,相對應的同級的光譜常數有明顯的差別(表2),從而導致了它們振動能譜的不同,即產生了同位素位移(表3)。該同位素位移的計算結果為探討通過測光譜的方法來測定CO同位素分子的應用技術提供了參考依據。

表 2 CO同位素分子X1∑+基態的振動光譜常數比較 cm-1

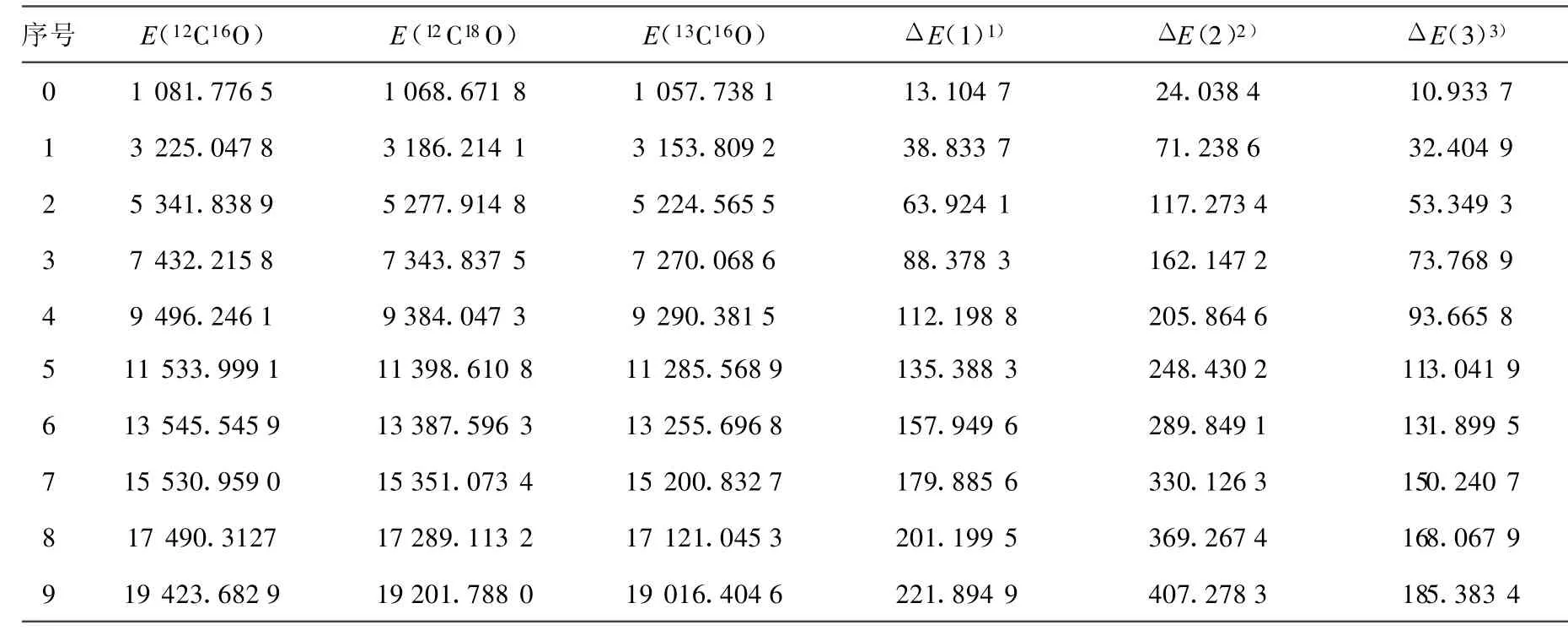
表3 CO同位素分子X1∑+基態振動能譜的同位素位移比較 cm-1

[1] Furne JK,Sp ring field JR,H o SB,et al.Simp lification of the end-alveolar carbon monoxide technique to assess ery th rocy te survival[J].JLab Clin Med,2003,142:1.

[2] Telle H,Telle U.A simp le numerical treatment of the RKR potential integrals and its application to12C16O(X1∑+)[J].JMol Spectrosc,1981,85:248.

[3] 徐光憲,黎樂民.量子化學基本原理和從頭計算法[M].北京:科學出版社,1985.

[4] 徐克尊.高等原子分子物理學[M].北京:科學出版社,2000.

[5] 徐亦莊.分子光譜理論[M].北京:清華大學出版社,1988.

[6] Mchale JL.Molecular Spec troscopy[M].New Jersey:Prentice-Hall,1999.

[7] Herzberg G.Molecular spectra andmolecular structure I:Spec tra of diatomic molecu les[M].New York:Van Nostrand Company,Inc,1950.

[8] 周公度,段連運.結構化學基礎[M].北京:北京大學出版社,2008.

[9] Huxley P,Murre ll JN.G round-state diatomic potentials[J].JChem Soc Faraday Trans:II.1983,79:323-328.

[10]朱正和,俞華根.分子結構與分子勢能函數[M].北京:科學出版社,1997.

[11]Murrell JN,Sorbie KS.New analytic form for the potential energy curves of stab le diatomic states[J].J Chem Soc Faraday Trans:II,1973,7:1 552-1 557.

[12]Huxley P,Knowels DB,Murrell JN,et al.G roundstate diatom ic potentials.Part 2:Van der Waals molecu les[J].JChem Soc Faraday Trans II,1984,80:1 349-1 361.

[13]Sun Weiguo,H ou Shilin.Studies on the Vibrational and Rovibrational Energies and Vibrational Force Constants of Diatomic Molecular States U-sing A lgebraic and Variational Methods[J].J Mol Spectrosc,2002,215:93-105.

[14]孫衛國,侯世林.雙原子分子體系的振動結構研究[J].原子核物理評論,2002,19(2):91-94.

[15]Huber KP,Herzberg G.Molecular Spectra and Molecular Structure(IV),Constants of Diatomic Molecules[M].New York:Van Nostrand,1979.

[16]朱正和.原子分子反應靜力學[M].北京:科學出版社,1996.