考慮統(tǒng)計不確定性的結(jié)構(gòu)可靠度分析方法

呂大剛，宋鵬彥，王光遠

(哈爾濱工業(yè)大學 土木工程學院，150090哈爾濱，ludagang@hit.edu.cn)

考慮統(tǒng)計不確定性的結(jié)構(gòu)可靠度分析方法

呂大剛，宋鵬彥，王光遠

(哈爾濱工業(yè)大學 土木工程學院，150090哈爾濱，ludagang@hit.edu.cn)

為了充分研究統(tǒng)計不確定性對結(jié)構(gòu)可靠度的影響，本文將綜合考慮物理不確定性和統(tǒng)計不確定性，以Bayes理論為數(shù)學工具，對結(jié)構(gòu)的統(tǒng)計可靠度問題進行研究.首先對Bayes理論進行概括和總結(jié)，采用該理論對結(jié)構(gòu)工程中的統(tǒng)計不確定性進行建模和分析.然后研究考慮統(tǒng)計不確定性的結(jié)構(gòu)可靠度分析方法，給出考慮統(tǒng)計不確定性的各種結(jié)構(gòu)可靠性測度，并研究綜合考慮主觀不確定性與客觀不確定性的整體式與分離式可靠度計算方法.最后通過2個算例，分析了統(tǒng)計不確定性對結(jié)構(gòu)可靠度的影響.

隨機可靠度;統(tǒng)計可靠度;物理不確定性;統(tǒng)計不確定性;Bayes統(tǒng)計學

結(jié)構(gòu)工程中的隨機性包括物理不確定性、統(tǒng)計不確定性和模型不確定性，物理不確定性是指各種物理量(如荷載、材料強度、結(jié)構(gòu)尺寸等)的客觀變異性;統(tǒng)計不確定性是由于對物理量進行統(tǒng)計分析時缺乏足夠的樣本信息而產(chǎn)成的;模型不確定性則源于對復雜物理現(xiàn)象進行數(shù)學建模時的理想化假設.傳統(tǒng)的結(jié)構(gòu)可靠度理論屬于隨機可靠度理論，因為它處理的主要是物理不確定性問題;而經(jīng)典可靠度理論則更多地考慮統(tǒng)計和模型不確定性問題［1］.目前，在結(jié)構(gòu)可靠度理論的研究領域，對于考慮統(tǒng)計不確定性和模型不確定性的結(jié)構(gòu)統(tǒng)計可靠度問題，研究得還不充分，有必要將上述2個領域的可靠度問題和方法進行融合.

Egeland［1］較早注意到了結(jié)構(gòu)隨機可靠度與經(jīng)典統(tǒng)計可靠度2個學科之間的分野，并提出了將這2種理論進行融合的建議.對于模型不確定性對結(jié)構(gòu)可靠度的影響問題，國內(nèi)外結(jié)構(gòu)設計規(guī)范當前的統(tǒng)一處理方法是在考慮材料性能和幾何參數(shù)隨機性的抗力模型基礎上，引入一個考慮計算模式隨機性的隨機變量，以考慮模型不確定性的影響.對于考慮統(tǒng)計不確定性的結(jié)構(gòu)可靠度問題，目前國內(nèi)外研究較少.Greimann等［2］采用經(jīng)典統(tǒng)計學中的區(qū)間估計方法對統(tǒng)計不確定性進行定量化，提出帶有一定置信度的可靠度計算方法，并對某一桁架結(jié)構(gòu)進行了概率可靠性分析.Lemaire等［3］對統(tǒng)計數(shù)據(jù)不確定性對結(jié)構(gòu)可靠度的影響進行了初步研究.Igusa等［4］采用Bayes分析技術較系統(tǒng)地研究了結(jié)構(gòu)工程中的不確定性.Der Kiureghian 等［5－7］深入研究了在不完全知識狀態(tài)下結(jié)構(gòu)安全性的各種測度，研究了基于主觀認識上的統(tǒng)計不確定性對系統(tǒng)可靠度和時變可靠度的影響.Faber等［8－10］在工程概率決策分析中考慮了統(tǒng)計不確定性的影響，并采用Bayes技術對統(tǒng)計數(shù)據(jù)進行更新.從目前發(fā)展趨勢看，對于統(tǒng)計可靠度問題，Bayes統(tǒng)計學大有代替經(jīng)典統(tǒng)計學的趨勢，特別是隨著馬爾可夫鏈蒙特卡洛(Markov Chain Monte Carlo，MCMC)模擬法的快速發(fā)展，后驗統(tǒng)計量和預測分布的計算已不存在困難.

本文將綜合考慮物理不確定性和統(tǒng)計不確定性，以Bayes統(tǒng)計學為數(shù)學工具，對結(jié)構(gòu)的統(tǒng)計可靠度分析方法進行深入細致的研究.

1 統(tǒng)計不確定性的Bayes建模與修正

1.1 Bayes修正公式

在Bayes統(tǒng)計學中，Bayes公式通過來源于觀測數(shù)據(jù)的似然函數(shù)修正先驗概率分布，從而將主觀信息與客觀信息進行有機集成

確定先驗分布的方法主要有主觀先驗分布、擴散先驗分布、無信息先驗分布、共軛先驗分布等方法;似然函數(shù)是根據(jù)客觀信息通過似然原理確定的;后驗分布實際上是給定樣本觀測值x后θ的條件分布:f″Θ(θ|x)∝L(θ|x)f'Θ(θ)，后驗分布一旦得到，即可得到Θ的平均值和標準差等后驗統(tǒng)計信息.

1.2 統(tǒng)計不確定性的建模與分析

利用Bayes修正公式(1)可以對統(tǒng)計不確定性進行建模與分析.

設f(x，θf)為隨機向量X的聯(lián)合概率密度函數(shù)，θf為考慮統(tǒng)計不確定性的分布參數(shù).當隨機試驗的觀測值表現(xiàn)為等式觀測(例如混凝土強度的統(tǒng)計分析)時，似然函數(shù)L(θf)可以取為

式中x1，x2，…，xn是X的隨機抽樣的一組觀測數(shù)據(jù).

如果抽樣不是隨機的，則必須使用樣本值的聯(lián)合分布建立似然函數(shù)，此時可以通過對于x的不等式觀測(例如橋梁的荷載驗證試驗)來取代對于 x的直接觀測.假設不等式觀測事件為Ei={gi(xi)≤0}，i= 1，…，n，并假設 xi是統(tǒng)計獨立的，則有

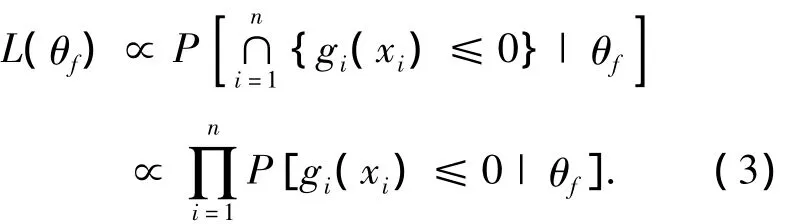
2 考慮統(tǒng)計不確定性的結(jié)構(gòu)可靠性測度

將統(tǒng)計不確定性參數(shù)記為θf，則考慮統(tǒng)計不確定性的結(jié)構(gòu)失效概率為

對于統(tǒng)計參數(shù)θf，通常有3種數(shù)學處理方法:點估計、區(qū)間估計和預測估計，相應地也有3種結(jié)構(gòu)可靠性的測度.

2.1 統(tǒng)計可靠度的點估計

式中Φ－1(·)為標準正態(tài)累積分布函數(shù)(CDF)的反函數(shù).

2.2 統(tǒng)計可靠度的區(qū)間估計

考慮某個統(tǒng)計參數(shù)θ∈θf，根據(jù)給定的置信水平α，尋求滿足式(6)的θ'和θ″，稱為θ的區(qū)間估計問題.

β的平均值和方差可按下式計算

式中 ▽θfβ(μθf)表示可靠指標 β 對向量 θf的梯度在μθf處取值.根據(jù)式(6)和式(7)即可得到可靠指標的區(qū)間估計為μβ±σβ.

2.3 統(tǒng)計可靠度的預測估計

根據(jù)Bayes統(tǒng)計學的基本原理，pf(θf)的Bayes估計為其后驗均值，即

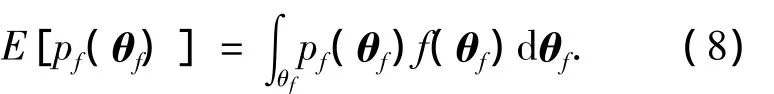
式中f(θf)為θf的后驗PDF.

根據(jù)Fubini定理，有

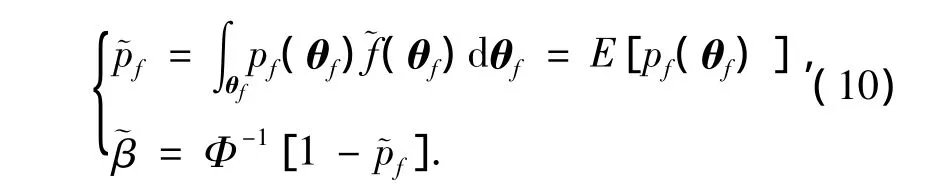
3 考慮統(tǒng)計不確定性的結(jié)構(gòu)可靠度分析方法

物理不確定性屬于客觀不確定性，而統(tǒng)計不確定性則屬于主觀不確定性.根據(jù)對于主觀和客觀不確定性數(shù)學處理方法的不同，結(jié)構(gòu)的統(tǒng)計可靠度分析有以下2種分析方法.

3.1 主觀與客觀不確定性的整體式分析方法

3.1.1 聯(lián)合分析(整體式分析方法1)

將θf與x同等對待，亦即將θf也視為隨機變量，將其與x連同一起組成擴展的隨機向量，然后采用經(jīng)典的隨機可靠度理論進行分析，失效概率為

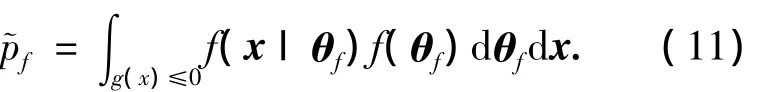
通常情況下，可以假設隨機向量x，θf相互獨立，于是可以采用經(jīng)典的FORM、SORM或重要抽樣(Importance Sampling，IS)等方法對式(11)進行一次隨機可靠度分析即可得到可靠指標和相應的失效概率.

3.1.2 預測分析(整體式分析方法2)利用x的預測分布來計算結(jié)構(gòu)的失效概率

將式(12)代入到式(11)中，可得到預測失效概率為

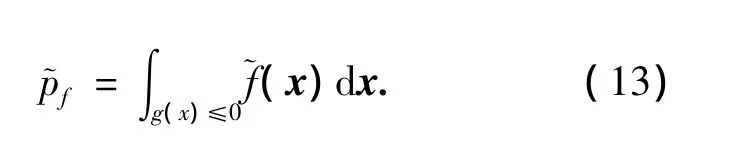
式(13)為給定當前樣本時，未來觀測值的預測失效概率.

3.1.3 嵌套分析(整體式分析方法3)

引入一個新的極限狀態(tài)函數(shù)

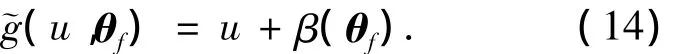
式中:u為標準正態(tài)隨機變量，并與 θf獨立;β(θf)為統(tǒng)計不確定性參數(shù) θf的條件可靠度指標.

相應于式(14)的失效概率為

由于u為標準正態(tài)隨機變量，因此上式中方括號內(nèi)的積分為

將式(16)代入式(15)，可得

3.1.4 近似分析(整體式分析方法4)

因此，預測可靠指標可以近似為

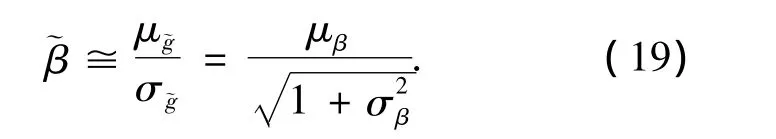
式中:μβ=E［β(θf)］，σβ為考慮主觀不確定性的可靠指標標準差，由式(7)求得.

3.2 主觀與客觀不確定性的分離式分析方法

與整體式分析方法同時處理主觀和客觀不確定性不同，這種方法將β(θf)單獨視為一個隨機變量進行統(tǒng)計可靠性分析.

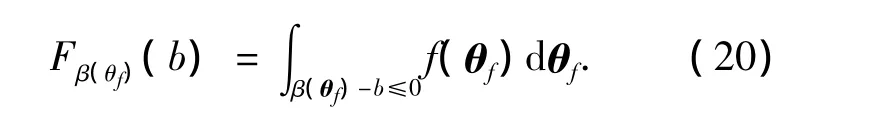
隨機變量β(θf)的累積分布函數(shù)(CDF)為顯然，這是一個嵌套可靠度分析問題，內(nèi)層需要首先計算 β (θf)，外層再計算 Fβ(θf)(b).

β(θf)的概率分布函數(shù)(PDF)為

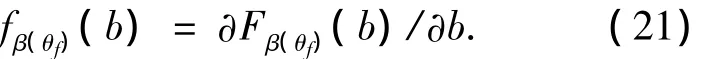
顯然，這是結(jié)構(gòu)可靠度理論中的靈敏度分析問題.

將 β(θf)在 M″θf處近似展開為一次 Taylor級數(shù)形式，可以得到β(θf)的一次近似為

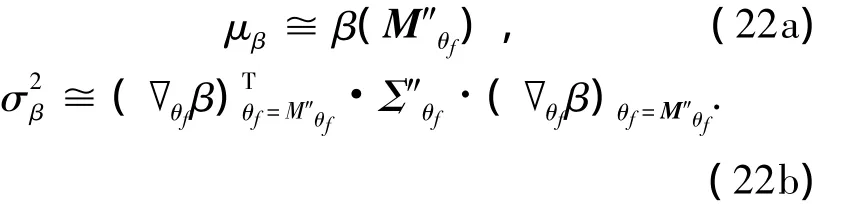
式中:M″θf為 θf的后驗平均值，Σ″θf為 θf的后驗協(xié)方差矩陣.

4 算例分析

4.1 數(shù)值算例分析

考慮極限狀態(tài)函數(shù)

式中:隨機變量 X1和 X2服從正態(tài)分布，即X1～N(μ1，σ1=20)，X2～ N(μ2，σ2=15).參數(shù)向量為θf= ［μ1，μ2］T，并且對于X1有n1個樣本，樣本均值1=100;相應的X2有n2個樣本，其均值為2=50.

這里假設均值μ1和μ2的先驗分布為無信息先驗分布，根據(jù)Bayes修正準則，可得后驗分布為

下面進行可靠指標的估計，根據(jù)可靠指標的定義有

4.1.1 可靠指標的點估計

依據(jù)式(7)和(24)，利用后驗均值可得可靠指標β的點估計值:

4.1.2 可靠指標的區(qū)間估計

根據(jù)分離式分析方法，利用μβ和σβ的一次近似，即由式(22)可得

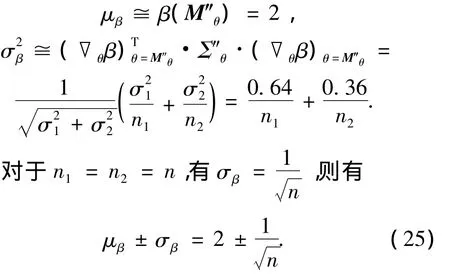
對n取不同值，由式(25)得可靠指標所在的區(qū)間，列入表1.

從表1可以看出，隨著樣本數(shù)的增加，由于統(tǒng)計不確定性所引起的可靠指標的變化范圍逐漸縮小，并向β的均值靠近.這說明，樣本數(shù)的增加使分布所含的統(tǒng)計不確定性減小，其可信程度提高，從而使β向真值靠近.

表1 可靠指標區(qū)間與樣本數(shù)n的關系

4.1.3 可靠指標的預測估計

根據(jù)Bayes原理，可得X1和X2的預測分布為

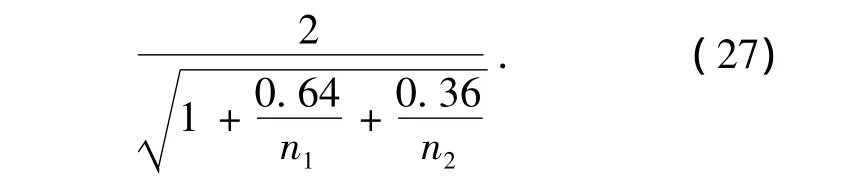
此外，也可以采用整體分析方法中的近似分析，即由式(18)可得

此式與式(27)等同.

由此可知，可靠指標與樣本的數(shù)量n1和n2有關，假設n1=n2=n，則式(27)可表示為

表2 預測可靠指標與樣本數(shù)n的關系

表2 預測可靠指標與樣本數(shù)n的關系

n 5 6 7 8 9 10∞1.826 1.852 1.871 1.886 1.897 1.907 2.000

4.2 考慮統(tǒng)計不確定性的斷裂可靠度分析

眾所周知，焊接的裂縫尺寸是隨機的.假設超過某一特定尺寸s0的概率密度函數(shù)

是關于參數(shù)θ的移位指數(shù)分布，希望在裂縫尺寸資料的基礎上對θ進行估計.假設通過對某一段焊縫觀測，參數(shù)θ的似然函數(shù)可表示為

當s0=0.1 cm，v=2 cm和k=11時，參數(shù)θ的后驗均值=k/v=5.5 cm－1，則可得裂縫尺寸的概率密度函數(shù)，如圖1所示.

由圖1可知，考慮θ不確定性的預測分布顯示極端裂縫尺寸的概率增大.

下面考慮壓力管道焊接裂縫的問題:假設管道長l=1 000 m，且焊接處產(chǎn)生的裂縫是均值比為λ的隨機泊松分布，希望確定焊接裂縫尺寸Smax的概率分布.一般從泊松分布中隨機抽取的分布其分布類型不變，由此可得

圖1 裂縫尺寸的概率密度函數(shù)

若已知Smax關于λ和θ的條件分布，則可得Smax的預測余累積分布函數(shù)(CCDF)，如圖2所示.圖中s0=0.1 cm，λ是服從參數(shù)k=10和v=120 cm的Gamma分布，θ也是服從參數(shù)k=11和v=2 cm的Gamma分布.由圖可知:考慮統(tǒng)計不確定性的結(jié)果降低了裂縫尺寸的概率.

圖2 最大裂縫尺寸的CCDF

5 結(jié)語

應用Bayes統(tǒng)計學，系統(tǒng)地研究了考慮統(tǒng)計不確定性的結(jié)構(gòu)統(tǒng)計可靠度理論，給出了考慮統(tǒng)計不確定性的各種結(jié)構(gòu)可靠性測度，并研究了綜合考慮主觀與客觀不確定性的整體式與分離式可靠度計算方法.通過算例分析表明，統(tǒng)計不確定性對只考慮客觀不確定性的隨機可靠度有很大影響.預計統(tǒng)計可靠度理論將會被廣泛應用于結(jié)構(gòu)的安全評定、健康監(jiān)測和壽命預測中.

［1］ EGELAND T.Two trends in reliability［J］.Structural Safety， 1991，9(4):261－268.

［2］ GREIMANN L F，KNAPP W J，YEUNG J Y．Propagation of certainty levels［J］．Journal of Structural Engineering， 1985，110(9):1935－1948．

［3］ LEMAIRE M，MOHAMED A，PENDOLA M，et al．Uncertainties in the treatment of statistical data and influences on the structural reliability assessment［C］//Proceedings of Lifetime Management of Structures．Paris:ESReDA，2003:98－108．

［4］ IGUSA T，BUONOPANE S G，ELLINGWOOD B R．Bayesian analysis of uncertainty for structural engineering applications［J］．Structural Safety， 2002，24(2/3/4):165－186．

［5］ DER KIUREGHIAN A．Measures of structural safety under imperfect states of knowledge［J］．Journal of Structural Engineering， 1989，115(5):1119－1140．

［6］ DER KIUREGHIAN A．Analysis of structural reliability under parameter uncertainties［J］．Probabilistic Engineering Mechanics， 2008，23(4):351 －358．

［7］ DER KIUREGHIAN A，DITLEVSEN O．Aleatory or epistemic?Does it matter?［J］．Structural Safety， 2009，31(2):105－112．

［8］ FABER M H，MAES M A．Epistemic uncertainties and system choice in decision making［C］//Proceedings of the 9th International Conference on Structural Safety and Reliability．Rome:ICOSSAR，2005:3519－3526．

［9］ FABER M H，MAES M A．Epistemic uncertainties in decision making［C］//Proceedings of the 24th International Conference on Offshore Mechanics and Arctic Engineering．Halkidiki:ASME，2005:1 －8．

［10］ FABER M H．On the treatment of uncertainties and probabilities in engineering decision analysis［J］．Journal of Offshore Mechanics and Arctic Engineering， 2005，127(3):243－248．

［11］ WEN Y K，CHEN H C．On fast integration for time variant structural reliability［J］．Probabilistic Engineering Mechanics， 1987，2(3):156－162．

Reliability analysis methods of structures considering statistical uncertainty

Lü Da－gang，SONG Peng－yan，WANG Guang－yuan

(School of Civil Engineering，Harbin Institute of Technology，150090 Harbin，China，ludagang@hit.edu.cn)

In order to fully investigate the influence of statistical uncertainty on reliability of structures，in this paper，the statistical reliability theory of structures considering two kinds of uncertainties，i.e.，physical uncertainty and statistical uncertainty，is deeply and thoroughly studied on the basis of Bayesian statistics.First，the fundamental principles of Bayesian statistics are summarized.The statistical uncertainty in structural engineering is then modeled and analyzed by Bayesian updating approach.The various measures for structural statistical reliability are introduced.After that，two methods for statistical reliability analysis of structures considering statistical uncertainty are proposed to treat with the aleatory and epistemic uncertainties:the integrated approach and the separate approach.Two examples are given，one of which is a numerical one;the other is a fracture reliability problem.The examples demonstrate the influence of statistical uncertainty on the reliability indices of structures.

random reliability;statistical reliability;physical uncertainty;statistical uncertainty;Bayesian statistics

TK124

A

0367－6234(2011)08－0011－05

2010－04－03.

國家自然科學基金重大研究計劃(90715021);

國家自然科學基金(50978080);

地震行業(yè)科研專項基金(200808073).

呂大剛(1970—)，男，教授，博士生導師;

王光遠(1924—)，男，教授，中國工程院院士.

(編輯 趙麗瑩)