普適計算環境下三維模型的錯誤保護編碼*

朱為鵬,羅笑南,3, 梁云

(1．中山大學信息科學與技術學院，廣東 廣州 510006；2．中山大學數字家庭教育部工程研究中心，廣東 廣州 510006；3．中山大學深圳研究院∥數字生活網絡與內容服務重點實驗室，廣東 深圳 518057；4．華南農業大學信息學院, 廣東 廣州 510642)

在普適計算環境下，無線信道是數據傳輸的主要通路。與有線信道相比，無線信道不僅噪聲大，而且具有多徑和陰影衰落，誤碼率高達10-3～10-5(有線信道的誤碼率一般在10-6以下)[1]。高誤碼率嚴重影響數據傳輸的質量，因此，三維模型編碼是否具有很強的抗誤碼能力是確保三維模型數據傳輸QoS的關鍵之一。

同時，為了節省寶貴的網絡帶寬資源，需要對三維網格模型數據進行壓縮。由于預測編碼和不定長熵編碼等壓縮編碼方案的使用，三維網格數據壓縮效率越高，其壓縮比特流對傳輸錯誤越敏感。隨機或突發的傳輸錯誤一旦發生，很可能在壓縮編碼數據中快速地傳播，造成嚴重的錯誤蔓延。

目前，關于改善三維網格模型數據誤碼彈性的研究很少。提高三角網格模型誤碼彈性所采用的方法主要是通過網格分片或分層等數據分割機制來阻止傳輸錯誤的蔓延。如：自適應的網格分割編碼等。受限于三維模型不規則的網狀拓撲結構，這些方法不僅操作比較復雜，對誤碼彈性的改善效果也不能令人滿意。

為此，本文提出了一種應用于普適計算環境下三維模型壓縮傳輸的錯誤保護 編碼方案。通過將三維網格模型編碼為規則采樣數據，三維模型網狀的拓撲連接關系被隱藏于完全規則的網格結構中，數據關聯性大為降低，三維模型的誤碼彈性得到了根本性改善；同時由于三維模型被均勻采樣為二維圖像數據，正交分析工具可直接運用，大大提高了壓縮效率。

1 相關工作

關于改善誤碼彈性的研究非常多[2-3]。但針對三維模型數據誤碼彈性的研究比較少，目前所采用的方法主要是通過網格分片或分層等數據分割機制來阻止錯誤蔓延超過塊邊界。如：MPEG-4中采用了基于組件的數據分塊策略(Component-Based Data Partitioning Scheme)來提高基于拓撲手術的三維網格模型壓縮編碼(TS-Based Coding)的誤碼彈性[4-5]。Li和Kuo[6-7]提出了一種建設性的遍歷編碼技術，在此基礎上，有一些基于網格分割策略的提高網格誤碼彈性 的研究[8-9]。其后，Yan等[10]提出了多點分塊機制(Multi-Seed Based Partitioning Scheme)來控制錯誤蔓延對壓縮的三維網格比特流的影響。Yan等[11]首先將可逆可變長編碼技術應用于三角網格編碼中。

Gu等[12]在2002年提出了一種構造全規則三角網格模型的重新網格化方法，可得到完全規則的網格模型。但是對于虧格高或有較長突起的模型來，會產生很高的參數化變形。為了減輕這種參數化變形，SANDER等提出了一種將模型參數化到平面上的多個任意邊界區域的多片式幾何圖像構造方法[13]。

2 編碼方案概述

本文提出了一種針對任意三維網格模型的均勻準保角平面參數化方法，可建立任意拓撲的三維網格模型與平面參數域之間的均勻準保角映射。再對參數域規則采樣，即可將三維模型幾何位置信息轉化為規則采樣的平面信號。

得到三維網格模型的規則采樣數據后，結合其自身特點并借鑒壓縮視頻流抗誤碼編碼技術，本文給出了基于錯誤保護的壓縮編碼方法，取得了編碼效率和錯誤彈性之間的平衡。

本文編碼方案的主要步驟如圖1所示。

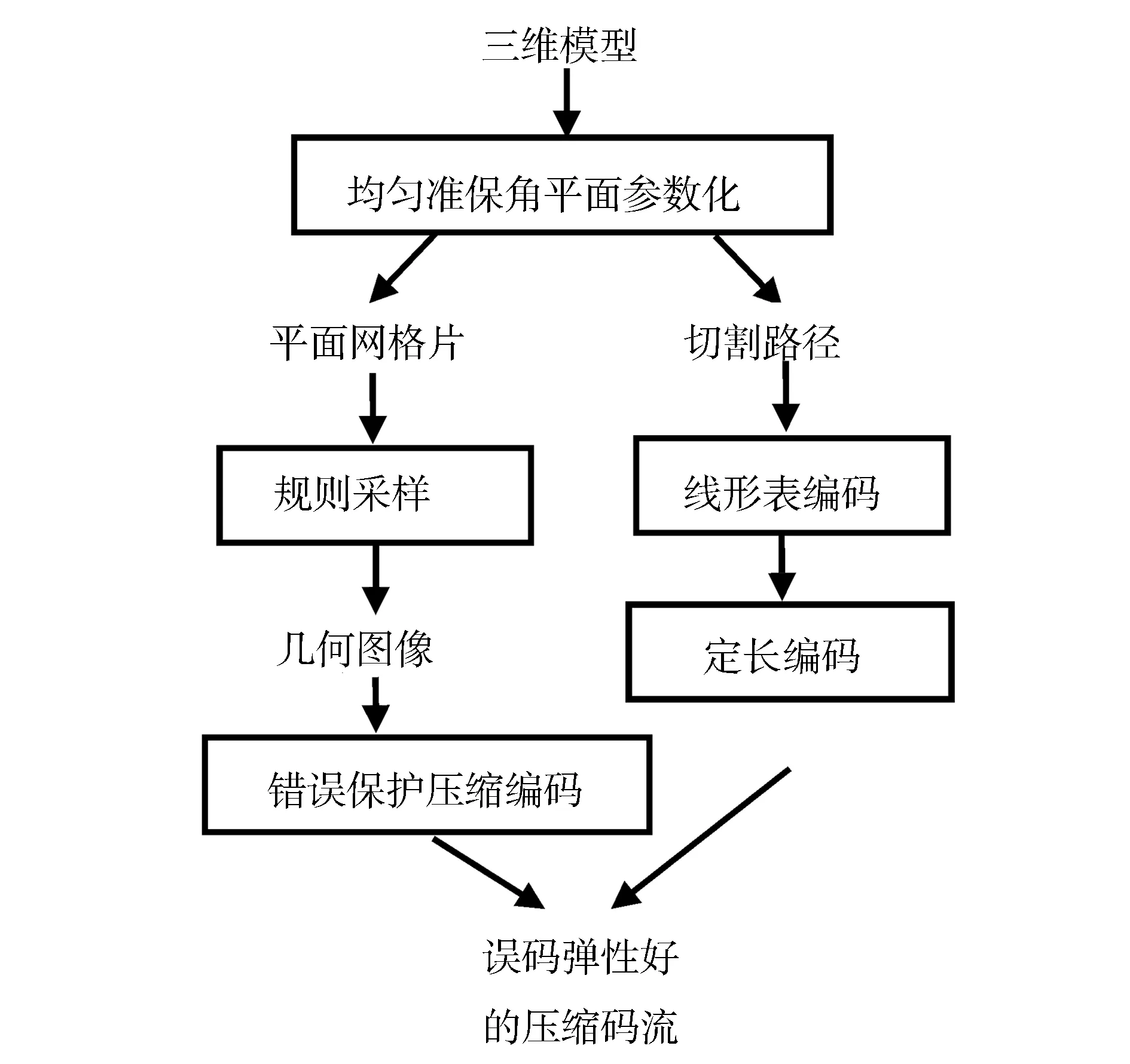
圖1 三維模型編碼方案流程圖

本文第三部分介紹三維模型的均勻準保角平面參數化方法并分析由此所得的三維模型規則采樣數據；第四部分介紹對三維模型規則采樣數據的所采取的基于錯誤保護的壓縮編碼方法；第五部分將本文所述的編碼方法應用于不同虧格和復雜程度的三維模型，通過模擬試驗得出本文編碼方案在誤碼彈性 和編碼效率方面的具體數據。

3 三維模型的規則采樣數據

一旦參數化過程中產生較大變形，參數域上均勻分布的采樣格點映射到三維模型時不能均勻分布，造成初始三維模型上大量特征丟失，導致規則采樣數據因不能忠實重建原始模型而失去價值。只有當參數化變形得到控制，參數域上均勻分布的采樣格點才能相對均勻的映射到三維模型(如圖2所示)。

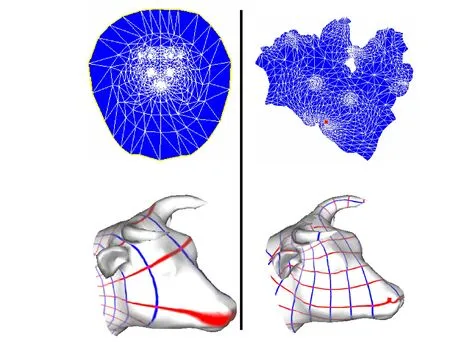
圖2 參數化變形對采樣點分布的影響(紅藍線的相交點即采樣點所在位置)

3.1 三維模型的均勻準保角平面參數化

出于盡量降低并控制參數化變形的目的，本文提出了一種均勻準保角平面參數化方法，步驟如下。

首先在初始三角網格模型上隨機選取一個非邊界的種子三角形，將其保長映射(完全無變形)到平面；然后從該三角形出發，依據局部幾何變形度量，每次選取一個變形最小的相鄰三角形展平，展平時保證所有三角形不重疊，直到所有相鄰三角形引入的參數化變形均大于預設值；再重新隨機選取種子三角形進行新一輪的展平，這樣每一次展平操作就生成一個新的準可展面片。

衡量局部三角形參數化變形程度時，假定T為原始三角網格模型上的一個三角形，T′為其二維平面上對應的映射，γmax和γmin為仿射變換Jacobi矩陣的最大和最小特征值，對應于原始平面上的不同位置單位長度在仿射變換之后長度的最大值和最小值。根據基于幾何變形(Geometric-stretch)度量空間的方法，三角形之間仿射變換的特征值度量空間定義如下

(1)

對于測量幾何失真來說，拉伸和收縮應一視同仁，因此Sorkine在文[7]中將局部三角形參數化變形定義改進為

D(T,T′)=max(γmax,1/γmin)

(2)

但這種定義方法僅用最大拉伸或最大收縮作為衡量參數化變形大小的指標，只能近似指示局部三角形角度和面積變形的大小。

考慮到從種子三角形開始的映射是保長的，即γmax與γmin值同為1，與其相鄰的三角形均有一條邊保持原長，因此，相鄰三角形若越近似于保角映射則局部三角形面積和角度的綜合參數化變形越小。以此類推，在隨后的展平過程中，每一次都是選取參數化變形最小且未超出預定閾值的相鄰三角形展平，對整個展平區域的映射可視為準保長，因此，仍可近似認為所有相鄰三角形中映射越接近于保角映射，其綜合參數化變形越小。

因此，我們定義局部三角形參數化變形為

D(T,T′)=γmax/γmin-1

(3)

當且僅當γmax等于γmin時，由T到T′的映射為保角映射。采用這種參數化變形度量方法，可更好的控制整體參數化誤差，保證每一步展開操作后得到準可展面片。

采用這種參數化方法創建規則采樣數據及重構三維模型的過程如圖3所示

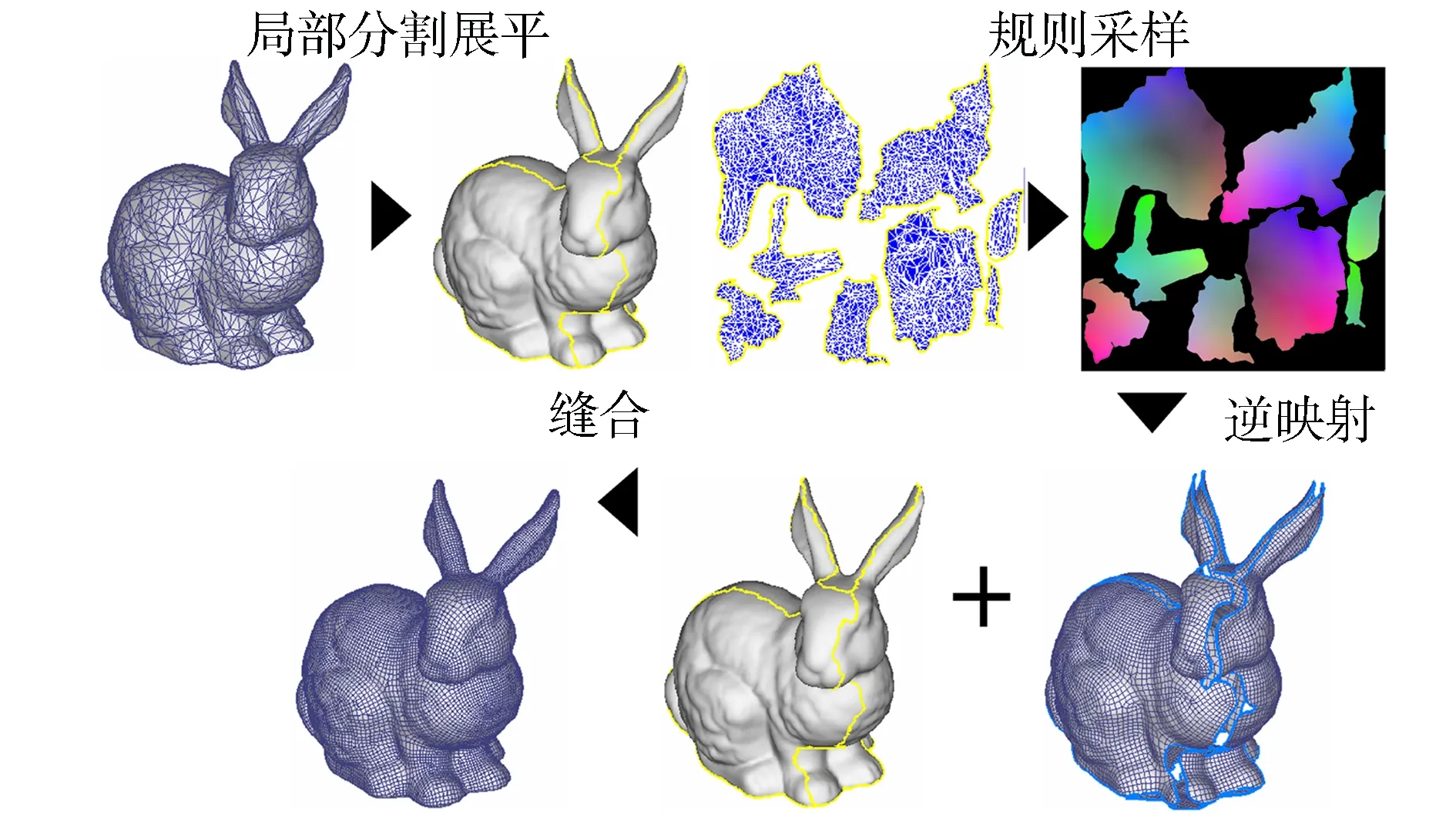
圖3 三維模型規則采樣數據的創建和三維重構

3.2 幾何圖像的數據結構

均勻采樣點的幾何位置信息由一個3×m×n數組來記錄。每個數組元素為一個浮點數；而切割路徑數據，則采用線性表來記錄，每個數據元素對應一個三維空間點，每一段切割路徑的結束用一個空數據元素來標記。

由于采用局部分割展平參數化方法，本文創建的幾何圖像上除了被定義的采樣點外，還包含未定義的點。因此我們還需要將未定義的點標識出來。

在區分未定義的點時，基于保持跟普通圖像數據在形式上一致同時節省存儲空間的考慮，采用的策略如下：設定值(0,0,0)只用于表示未定義的點。即將三維模型包絡體上坐標值最小的一個頂點設定為坐標原點，如果該點同時也是網格模型上的一個頂點，就將該點移動到(-Max(x)/1 000,0,0)，并將該點移動后所至的位置作為新的坐標原點。這樣就可確保坐標值(0,0,0)不在三維模型的表面。

根據以上分析可知，本文算法所得幾何圖像的文件結構如下：幾何圖像文件的第一部分記錄網格模型規則采樣點的幾何位置信息，數據結構為一個3×m×n數組；第二部分記錄切割路徑信息，數據結構為線性表。除此之外，還可以數組的形式記錄規則采樣點的其他表面幾何信息，如紋理和法向方向等。

3.3 幾何圖像數據的誤碼彈性

評價數據誤碼彈性的主要指標包括數據關聯程度和數據相關性。

數據關聯是指數據之間相互依賴的程度，即數據的正確解碼是否需要依賴其它數據。它是通信錯誤在數據間擴散造成數據傳輸質量急劇下降的直接原因。數據編碼的關聯性越強，其誤碼彈性越差。

數據相關性是指相鄰數據之間的變化比較平滑，并且有一定的規律。它同時也體現了信息在結構上的冗余程度。如果數據相關性強，一旦傳輸錯誤發生，在錯誤隱藏與恢復階段，就可以利用周圍正確傳輸的數據隱藏數據異常或缺失，較好地恢復正確的數據。

提高誤碼彈性的關鍵是降低數據之間的關聯程度，同時盡量保持其相關性。以三角網格模型的幾種主流文件格式obj, wrl, ply為例：三角網格模型數據文件的主體都是由頂點元素列表和面元素列表兩部分組成，其中頂點元素列表記錄三維網格模型的幾何信息：即各頂點在三維空間的位置；面元素列表記錄三維網格模型的拓撲信息，通過列出組成每個三角面片的頂點序號，記錄頂點之間的拓撲連接關系。頂點表和面表都是無序的，可隨意改變頂點表內元素的排列順序(面表的內容作相應改變)或面表內元素的排列順序。因此，三角網格模型數據之間不存在相關性。

同時，面表(拓撲連接信息)的正確解碼必須依賴于完全正確的頂點元素列表。如果頂點元素列表的傳輸出現錯誤，拓撲連接信息就有可能出錯，特別是一旦頂點元素列表的序號出現錯誤，將導致整個網格結構的破壞。

對于幾何圖像數據，由于拓撲連接關系被隱藏于完全規則的網格結構，而幾何位置信息在均勻采樣后，被存儲為類似于圖像的矩陣方式，具有相鄰的矩陣序號的元素對應空間上相鄰的點，因此數據之間的相關性較強。

以上對三角網格數據和幾何圖像數據的數據關聯性和相關性的分析結果如表1所示。

表1 幾何圖像和三角網格數據誤碼彈性分析

由此可見，將三角網格模型編碼轉化為幾何圖像編碼后，數據關聯程度隨之大為降低，同時數據相關性增強。這使得幾何圖像數據形式在誤碼彈性上與三角網格數據形式相比有明顯的優勢。

4 基于錯誤保護的幾何圖像壓縮編碼

本節主要討論基于錯誤保護的幾何圖像壓縮編碼方法。與普通的圖像數據相比，本文方法的創建幾何圖像數據具有以下特點

1)幾何圖像呈現為邊界清晰的數片；背景部分對應未定義的點，值均為(0,0,0)；

2)每片圖像數據對應于三維模型上某一片模型表面幾何信息的規則采樣，片內數據相關性很強，有較大的空間冗余，即在相鄰像素間、相鄰行間存在著強相關性；

為了去除大部分的背景區域，本文采用了簡單的數據分塊策略：將圖像分割成8×8的小塊，按照從左到右，從上到下的順序記錄每小塊的序號，對于只包含背景，即值均為(0,0,0)的圖像，無需做進一步處理。這些區域在全部數據解碼之后，直接填入(0,0,0)值即可。如圖4所示。

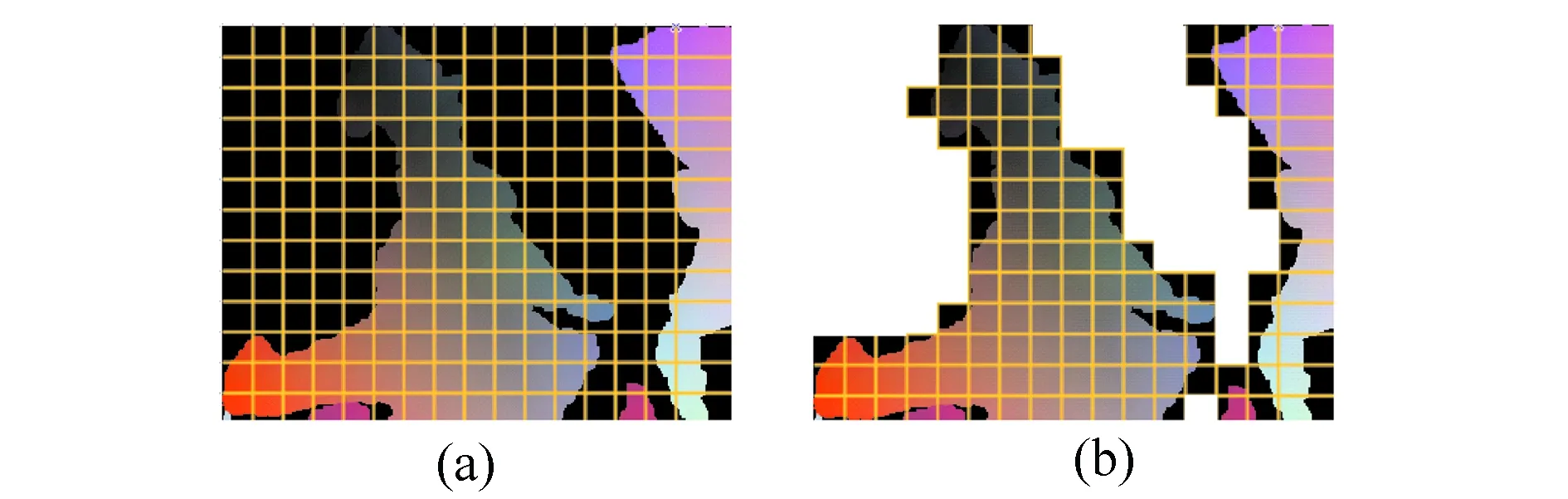
圖4 (a)圖像分塊 (b)背景剔除

要消除相鄰像素間、相鄰行間存在的強相關性，必須采用變換編碼，通過將圖像能量在空間域的分散分布變為在變換域的相對集中分布，獲得對圖像信息的有效壓縮。

常用的變換編碼有K-L變換編碼，離散余弦變換(DCT)編碼和小波變換編碼。K-L變換編碼理論上可以得到最優的壓縮比，但其運算量過大。離散余弦變換(DCT)編碼最接近最佳K-L變換，相關理論成熟，有快速算法，且適用于圖像的分塊壓縮。采用這種方法，對于幾何圖像這種空間冗余較大的數據，可以達到良好的去相關性和能量集中效果，如圖5所示。

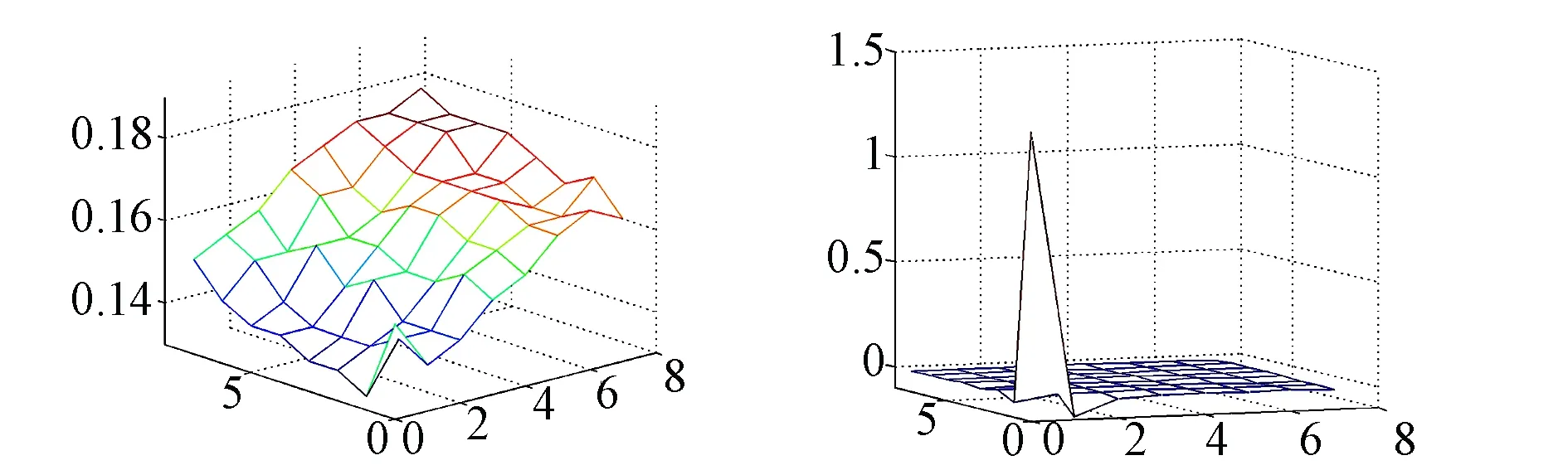
圖5 (a)輸入的8×8圖像塊矩陣(b)DCT變換得輸出矩陣

由以上變換的結果可知：0行0列具有的DCT系數比其它DCT系數大得多，它稱作直流(DC)系數。其余系數稱為交流(AC)系數。AC系數的值隨著它與DC系數的距離增加而越來越小。在作一般圖像有損壓縮時，僅保留直流系數和左上角的交流系數就能夠保留大部分的圖像信息，從而達到大幅度壓縮圖像的目的。為了確保壓縮舍入誤差得到較好控制，不影響后續三維重構，本文對交流系數采取了如下近無損量化方法

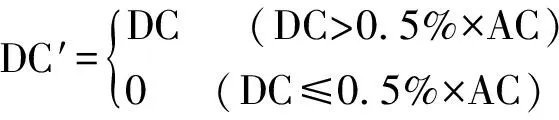
(4)

經過DCT變換和近無損量化后，每個圖像塊需編碼的信息如下：圖像塊的序號、直流系數和交流系數。有于圖像塊的序號非常重要，同時誤碼彈性 圖像編碼要求直流系數不應相互依賴。由此，一種定長編碼(FLC)就被用于編碼塊序號和直流系數，對交流系數，就采用霍夫曼(Huffman)編碼。這樣每個圖像數據塊由定長編碼的塊序號和霍夫曼編碼的交流系數組成，塊與塊之間插入可選擇的重置標志碼(RSTm標志碼)，將傳輸誤差控制在塊邊界內。

整個基于錯誤保護 的幾何圖像數據的壓縮編碼過程如圖6所示。

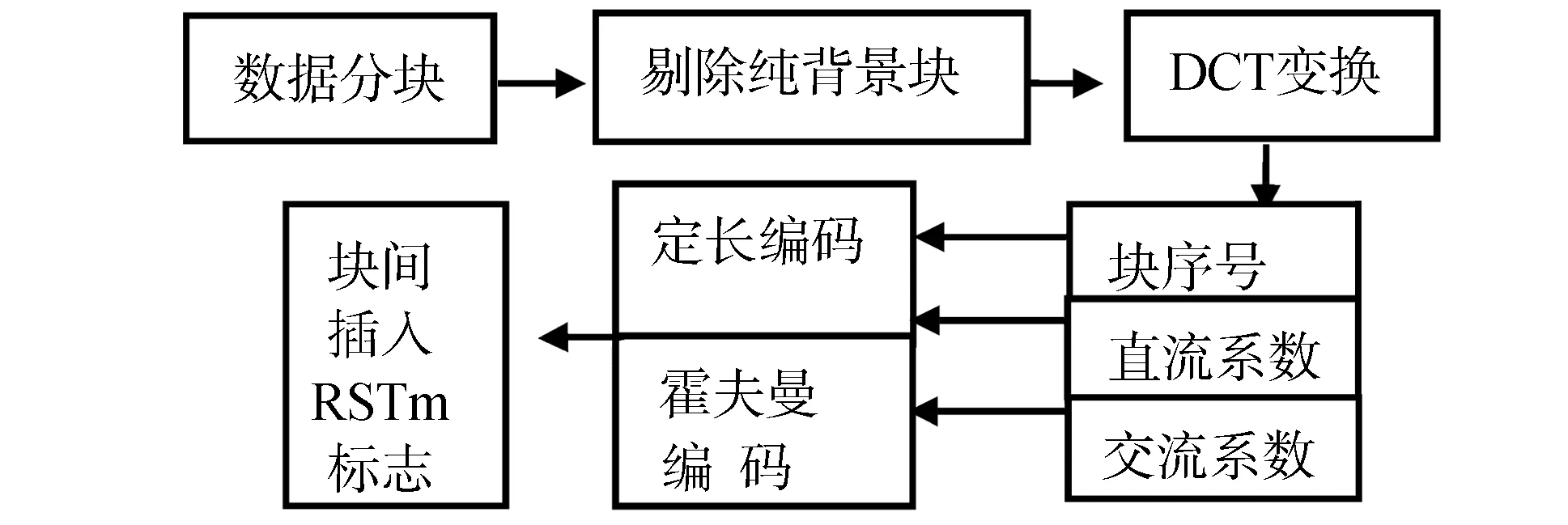
圖6 基于錯誤保護的幾何圖像壓縮流程

通過去除背景數據塊，以及對圖像做分塊DCT變換，近無損量化，并對交流系數霍夫曼編碼，幾何圖像數據的大部分冗余被去除，實驗數據表明壓縮比可達3.8～9.4之間；同時數據分塊，對塊序號、直流系數定長編碼，并在塊之間加入RSTm標志等措施，使幾何圖像數據得到了有效的錯誤保護。

5 試驗結果與分析

為了得到本文所述的編碼方法在誤碼彈性和編碼效率方面的具體表現，我們選擇了不同虧格、不同復雜程度的模型，進行了大量的實驗。

實驗結果驗證了本文方法的廣泛適用性：對于高虧格或有較長突起的模型，根據幾何圖像重構的模型仍能較好的保持初始模型特征，如圖7所示。

將本文所述的幾何圖像壓縮編碼方法應用于不同數據規模的模型，所得到的結果表明：相對于三角網格數據，幾何圖像數據所需的存儲空間均比三角網格數據小，且具有更好的可壓縮性能。具體數據如表2所示。

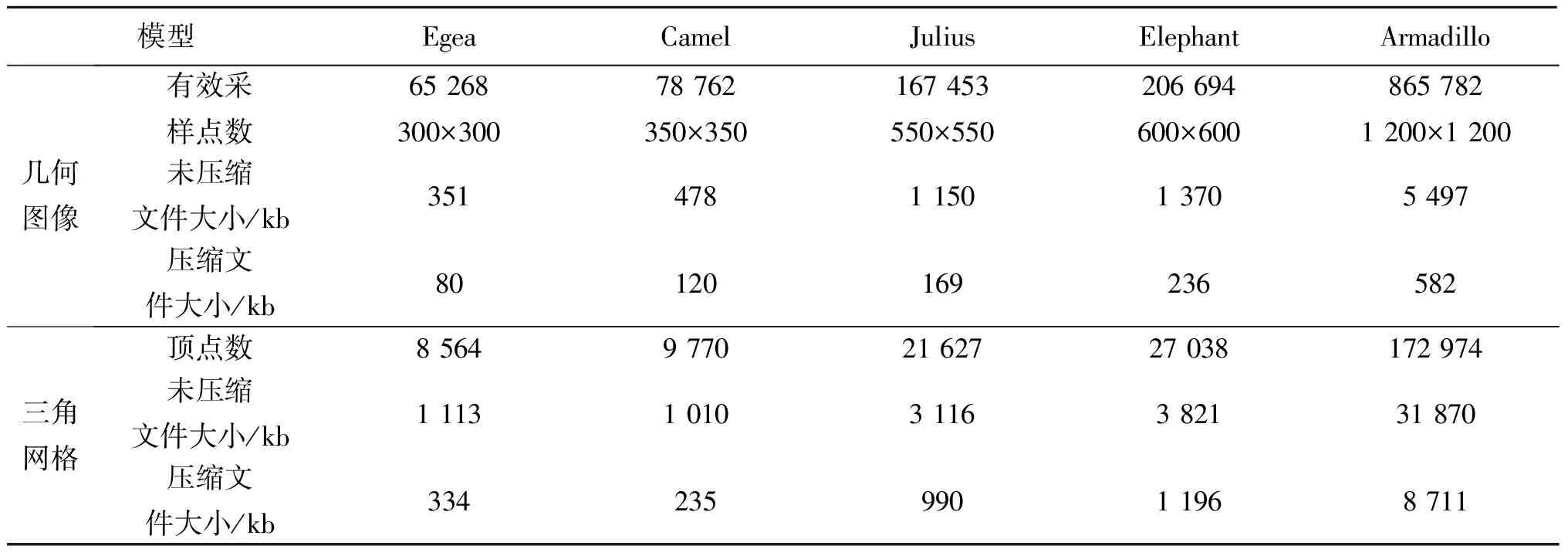
表2 幾何圖像與三角網格所需的存儲空間對比

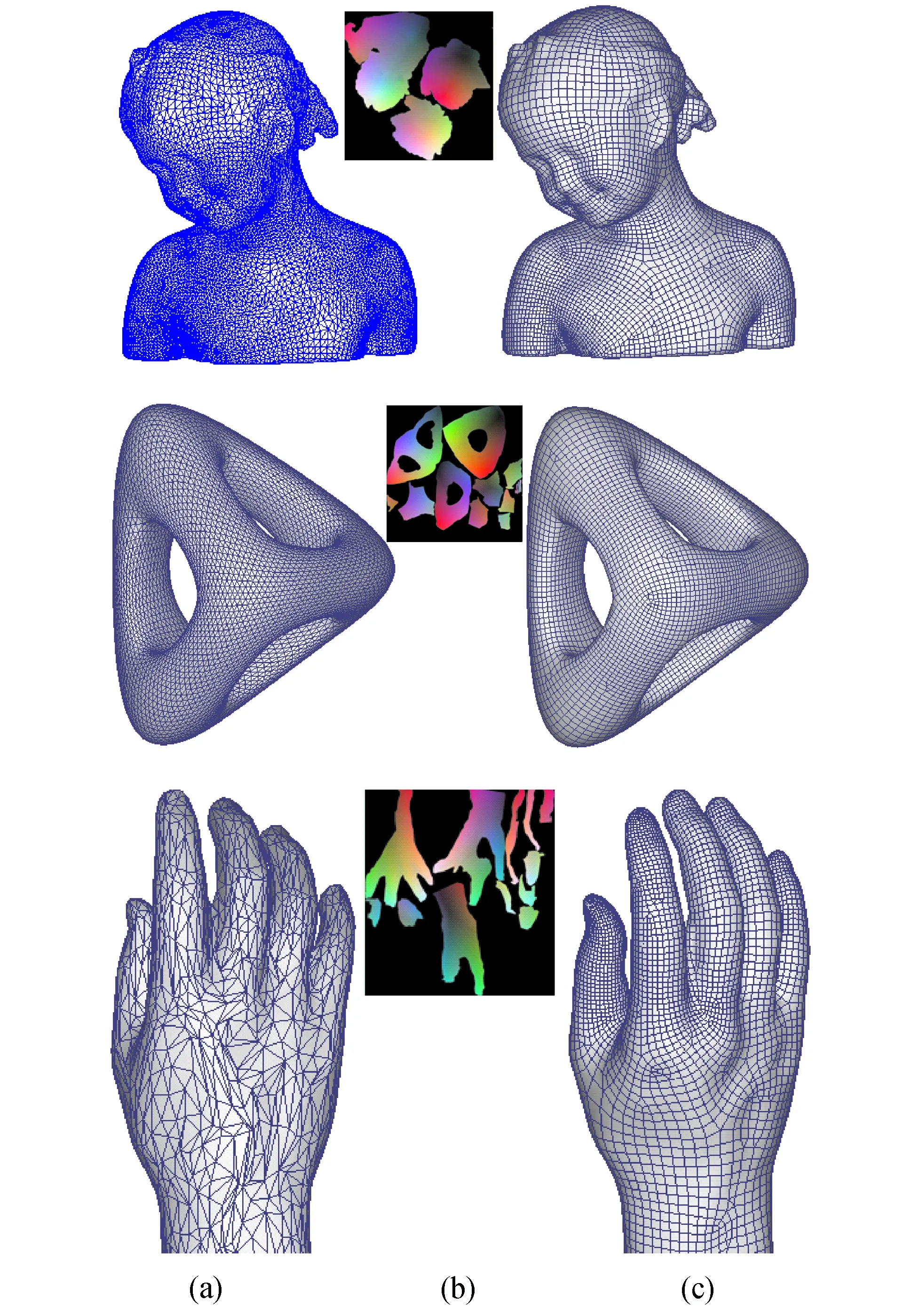
圖7 (a)初始模型；(b)幾何圖像；(c)重構模型

為了得到本文方法在誤碼彈性方面的具體表現，本文以五組三維模型作為測試數據，分別采用的幾何圖像和傳統的三角網格進行編碼，各進行了500次模擬傳輸實驗。傳輸速率約為256 kbits/s，分別以10-2、10-3、10-4、10-5隨機產生的脈沖信號作為加性噪聲表示不同的隨機誤碼率。

所得具體實驗數據如表3所示(其中GI為幾何圖像，GI_C為采用本文方法壓縮的幾何圖像，TM為三角網格，TM_C為rar壓縮的三維網格)。

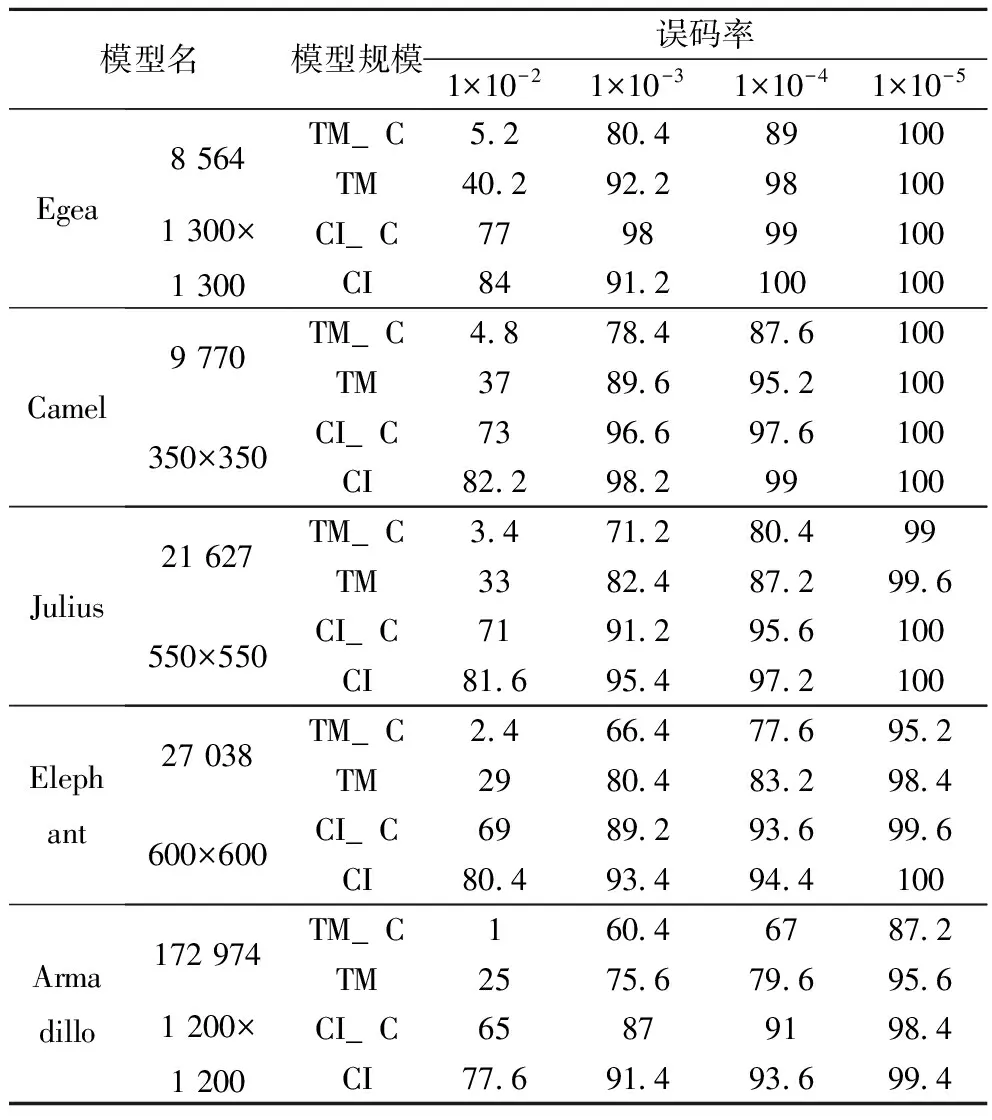
表3 三維模型在不同隨機BERs下的傳輸正確率

6 結 論

為了解決普適計算環境下傳輸信道誤碼率較高，同時三角網格模型不規則的網狀結構對于傳輸錯誤又非常敏感的矛盾，本文提出了一種基于幾何圖像的三維模型錯誤保護編碼方法。

采用本文提出的均勻準保角平面參數化方法對模型做低誤差的參數化處理，三維模型的幾何信息可被均勻的采樣，并進一步編碼為二維圖像的方式。隨著其不規則的網狀結構消除，模型數據之間關聯性大大降低，同時相關性增強。因此這種編碼的三維模型數據，其誤碼彈性可得到根本改善。

為了節省普適計算環境下的網絡帶寬資源，進一步提高編碼效率，本文還給出了基于錯誤保護的壓縮編碼方案，取得了編碼效率和誤碼彈性之間的較好平衡。模擬試驗的結果表明，與常規的三角網格編碼方法相比，這種編碼方法從根本上改善了三維模型數據的誤碼彈性，并只需較少的存儲空間。

這種編碼方法的主要不足如下：在構造三維網格模型的規則采樣數據時，目前采用的參數化方法雖可確保參數化誤差較小且可控，但造成三維模型切割路徑較長，導致以下兩個問題：①在傳輸終端，根據規則采樣數據重構三維模型時，模型片縫合步驟計算復雜且耗時較多；②在構造三維網格模型的規則采樣數據時，當采樣密度較低時，會造成重構模型上明顯的縫合痕跡和變形。

因此下一步的研究工作應包括兩方面：一方面要研究新的平面參數化方法，在確保參數化誤差較小的同時盡量減少切割路徑，致力于解決上述問題；另一方面應借鑒圖像與視頻最新的錯誤保護和壓縮編碼方法，對三維網格模型的規則采樣數據進行更高效的基于錯誤保護的壓縮編碼。

參考文獻：

[1]HAN Y H, LEOU J J.Detection and correction of transmission errors in JPEG images [J].IEEE Transactions on Circuits and Systems for Video Technology, 1998, 8(2): 221-231.

[2]趙慧民,方艷梅.率失真最優自適應量化及其系數閣值的設定[J].中山大學學報：自然科學版, 2004, 43 (3) : 32-35.

[3]趙慧民, 方艷梅.一種非均勻錯誤保護實現最優碼率分配的技術[J].中山大學學報：自然科學版, 2007, 46(1): 43-47.

[4]ZHANG Q, LIU G.Error resilient coding of H.264 using intact long-term reference frames [C]∥Visual Information Engineering, 2008: 62-66.

[5]AL-REGIB G, ALTUNBASAK Y, ROSSIGNAC J.A joint source and channel coding approach for progressively compressed 3-D mesh transmission [C]∥ICIP, 2002: 161-164.

[6]HAN M J, SONG M S, KIM S J, et al.Results of M5 code-experiments [C]∥ISO/IEC JTC1/SC29/WG11, MPEG98/M4516, 1999.

[7]PARK S B, KIM C S, LEE S U.Error resilient 3-D mesh compression [J].IEEE Transactions on Multimedia, 2006, 8(5): 885-895.

[8]YAN Z D, KUMAR S, KUO C C J.Error-resilient coding of 3-D graphic models via adaptive mesh segmentation [J].IEEE Transactions on Circuits and Systems for Video Technology, 2001, 11(7): 860-873.

[9]YAN Z D, KUMAR S, LI J, et al.Error resilient coding of 3D graphics based on morphing and volume splitting [C]∥SPIE Int Symp Voice, Video and Data Communications, Boston, MA, 1999: 128-136.

[10]YAN Z D.Efficient and robust compression on 2D and 3D graphics [D].Los Angeles: Univ of Southern California, CA, 1999.

[11]YAN Z D, KUMAR S, LI J, et al.Reversible variable length codes (RVLC) for robust coding of 3D topological mesh data [C]∥Proc Data Compression Conference ’99, 1999: 560-566.

[12]GU X, GORTLER S, HOOPE H.Geometry images [C]∥ACM SIGGRAPH 2002, 355-361.

[13]SANDER P, WOOD Z, GORTLER S, et al.Multi-chart geometry images [C]∥Eurographics Symposium on Geometry Processing, 2003:146-152.