求解大規(guī)模線性時不變系統(tǒng)的最優(yōu)2模型降階問題的共軛梯度法*

曾泰山，魯春元，陳 劍

(1.中山大學(xué)數(shù)學(xué)與計算科學(xué)學(xué)院，廣東 廣州 510275；2.廣東藥學(xué)院醫(yī)藥信息工程學(xué)院，廣東 廣州510006;3.佛山科學(xué)技術(shù)學(xué)院數(shù)學(xué)系，廣東 佛山528000)

近年來，模型降階越來越受到重視。它可以大大降低大規(guī)模系統(tǒng)模擬和控制中的時間復(fù)雜度，在超大規(guī)模集成電路設(shè)計，實時控制，天氣預(yù)報等領(lǐng)域有著重要應(yīng)用。關(guān)于模型降階的綜述，參見文獻(xiàn)[1-2]。

給定矩陣A∈Rn×n，B∈Rn×p和C∈Rq×n，線性時不變系統(tǒng)可以表示成：

(1)

y(t)=Cx(t)

(2)

其中t≥0表示時間變量，u(t)∈Rp表示輸入，y(t)∈Rq表示輸出，x(t)∈Rn表示系統(tǒng)的狀態(tài)。n是系統(tǒng)的階。p和q是系統(tǒng)的輸入和輸出個數(shù)。當(dāng)系統(tǒng)的階n很大的時候，由于需要大規(guī)模計算和存儲，這使得系統(tǒng)的數(shù)值模擬和控制非常困難。解決這一問題的一種關(guān)鍵方法是構(gòu)造一個低階的系統(tǒng)去逼近原始的高階系統(tǒng)，并保持相應(yīng)的系統(tǒng)特性。

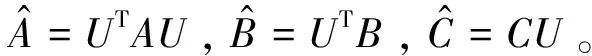
(3)

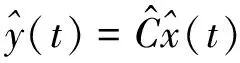
(4)

定義全階系統(tǒng)(A,B,C)的傳遞函數(shù)為

G(s)=C(sI-A)-1B,s∈C

方程 (3) 和 (4) 描述的降階系統(tǒng)的傳遞函數(shù)為

CU(sI-UTAU)-1UTB,s∈C

(5)

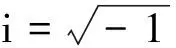
CU(sI-UTAU)-1UTB

(6)

定義代價函數(shù)

(7)

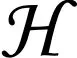
(8)

[U]:={UQm|Qm∈Om}

其中,Om表示所有m×m正交矩陣構(gòu)成的正交群，U∈Rn×m滿足UTU=I。由定義可知，等價類[U]中的矩陣的列向量張成的線性子空間相同。 在實際計算中，我們將選擇其中一個正交矩陣U∈Rn×m來代表整個等價類。關(guān)于Grassmann流形的幾何性質(zhì)，參看文獻(xiàn) [10-11]。

由方程 (6) 以及代價函數(shù)J(U)的定義 (7)可以看出

J(U)=J(UQm),?Qm∈Om

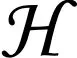
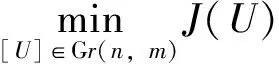
(9)

通過利用 Grassmann 流形的幾何性質(zhì)，我們將提出求解問題 (9) 的數(shù)值算法。

在 (6) 定義的誤差傳遞函數(shù)Ge(s)可改寫為

Ge(s)=Ce(sI-Ae)-1Be,s∈C

實際上，矩陣Ae，Be和Ce定義了一個系統(tǒng)實現(xiàn)為(Ae,Be,Ce)的誤差系統(tǒng)。Ge稱為是誤差系統(tǒng)的傳遞函數(shù)。誤差系統(tǒng)的可控性Gramian矩陣Ec和可觀測性Gramian矩陣Eo由如下的Lyapunov方程所定義

(10)

(11)

我們將可控性Gramian矩陣Ec和可觀測性Gramian矩陣Eo做如下分劃

∑c,∑o∈Rn×n,P,Q∈Rm×m

Lyapunov方程 (10) 和 (11) 可以轉(zhuǎn)化為

A∑c+∑cAT+BBT=0

(12)

AT∑o+∑oA+CTC=0

(13)

UTAUP+PUTATU+UTBBTU=0

(14)

UTATUQ+QUTAU+UTCTCU=0

(15)

AX+XUTATU+BBTU=0

(16)

ATY+YUTAU-CTCU=0

(17)

代價函數(shù)J(U)可以用Gramian矩陣Ec表示如下[9]

trace[CTC(∑c+UPUT-2XUT)]

(18)

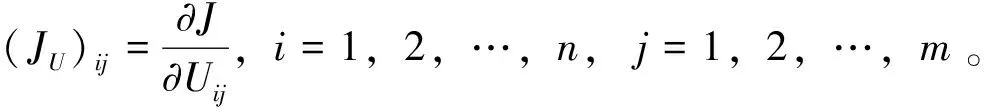
R:=AT[U(YTX+QP)]+A[U(XTY+PQ)]+

CT[C(-X+UP)]+B[BT(Y+UQ)]

(19)

代價函數(shù)J(U)在點(diǎn)U的偏導(dǎo)數(shù)為

JU=2R

由參考文獻(xiàn) [11]， 在點(diǎn)[U]∈Gr(n,m)處的切空間T[U]Gr(n,m)可以表示為

T[U]Gr(n,m)={ξ∈Rn×m|UTξ=0}

代價函數(shù)J的梯度▽J∈T[U]Gr(n,m)為

▽J=R-UUTR

(20)

2 共軛梯度法

下面我們給出共軛梯度算法的概要。假設(shè) (A,B,C) 是全階系統(tǒng)的狀態(tài)空間實現(xiàn)。記Uk為第k步獲得的模型降階投影矩陣，k=0,1,…。在共軛梯度算法中，通過以Uk為起點(diǎn)，以Fk為方向的測地線上搜索得到下一個投影矩陣Uk+1。流形上的測地線流形上兩點(diǎn)最短路徑。以Uk為起點(diǎn)，方向為Fk的Grassmann流形的測地線為

(21)

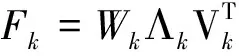
(22)

為了計算下一步的搜索方向Fk+1，首先計算在點(diǎn)Uk+1處的梯度Gk+1=▽J(Uk+1)。通過求解以下的Sylvester方程來計算矩陣Pk+1，Qk+1，Xk+1和Yk+1，

(23)

(24)

(25)

(26)

矩陣Rk+1為

(27)

在點(diǎn)Uk+1偏導(dǎo)數(shù)JUk+1為JUk+1=2Rk+1。代價函數(shù)J在點(diǎn)[Uk+1]∈Gr(n,m)的梯度為

下面將介紹共軛梯度法的搜索方向構(gòu)造。計算舊搜索方向Fk的平行移動

選取新的搜索方向為共軛梯度方向，即舊搜索方向的平行移動和新的梯度的線性組合

Fk+1=-Gk+1+γkτFk

(28)

在式子 (28)中，τFk為切向量Fk的沿著測地線的平行移動。切向量在流形上的平行移動是歐氏空間中向量平移的推廣。類似于歐氏空間中共軛梯度法，組合系數(shù)γk可以通過下面的式子(Polak-Ribiere法則)得到

γk=/

(29)

其中τGk是梯度Gk的平行移動

τGk=Gk-(UkVksin(tkΛk)+

值得指出的是，如果令γk=0，則Fk+1=-Gk+1，即搜索方向為負(fù)梯度方向，此時共軛梯度法就退化為文獻(xiàn)[7]中的梯度流算法。

下面是本文提出的共軛梯度法(CGA)的主要框架。

Algorithm 1: 共軛梯度法(CGA)

2)Fork=0,1,2,…,N-1

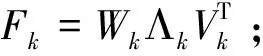
b)求解極小化問題

(30)

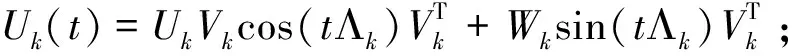
c)計算梯度Gk+1=▽J(Uk+1)；

d)平行移動切向量Fk和Gk到點(diǎn) [Uk+1]:

計算新的搜索方向

其中

Endfor

3) 獲得投影矩陣U=UN，計算

在上述算法中，需要求解極小化問(30)，這可以通過不完全線性搜索算法來求得，例如Armijo 搜索方法，可參見文獻(xiàn) [10]。

對于Grassmann 流形上的最優(yōu)化問題，共軛梯度法在滿足一定的條件下達(dá)到超線性收斂[10-11]。因此，本文提出的共軛梯度算法也能達(dá)到超線性收斂。

另外，由于本文所提出的共軛梯度算法不需要求解大規(guī)模的 Lyapunov 方程，因此計算量大大減少。下面，我們來分析共軛梯度算法的計算復(fù)雜性。在本文中，將以乘法次數(shù)來衡量計算復(fù)雜性。記Ns極小化問題 (30) 的最大搜索步數(shù)。記N為最大迭代次數(shù)。

定理1 假設(shè)A∈Rn×n是個具有N(A)個非零元素的稀疏矩陣。假設(shè)存在一個只需要O(rn+N(A))次乘法運(yùn)算的線性方程求解方法求解方程

(A-ηI)x=b,η?σ(A),b∈Rn

(31)

其中r是個固定的整數(shù)。則共軛梯度法CGA計算復(fù)雜度為

O(N(nmr+mN(A)+Nsnm2+nmp+nmq))

證明 在第k步迭代中，k=0,1,…，算法 CGA 的計算花費(fèi)主要來自以下三個方面：

第一部分是Pk、Qk、Xk和Yk的計算，需要求解Sylvester方程 (23)-(26)。在文獻(xiàn)[7]中指出，如果存在一個只需要O(rn+N(A))次乘法運(yùn)算的方法求解方程 (31)，則利用文獻(xiàn)[12]中的方法求解 Sylvester 方程 (23)-(26) 的計算復(fù)雜度只需

O(nmp+nmq+nmr+mN(A)+m3)

第二部分是搜索方向Fk的計算。對給定的A，B，C和Uk，需要O(mN(A)+nm2+nmp+nmq)次乘法運(yùn)算來計算Rk。因此，它需要O(mN(A)+nm2+nmp+nmq)次乘法運(yùn)算來計算Fk。

第三部分是非精確搜索方法求解最小化問題 (30) 以獲得步長tmin。對極小化問題 (30) 的每一個搜索步，我們需要計算測地線方程 (21)。易知，測地線的計算復(fù)雜度為O(nm2)。 因為最大的搜索步數(shù)為Ns，所以非精確搜索方法求解最小化問題 (30) 的計算復(fù)雜度為O(Nsnm2)。

總而言之，算法CGA每一步迭代需要O(nmr+mN(A)+Nsnm2+nmp+nmq) 次乘法次數(shù)。由于算法CGA的最大迭代次數(shù)為N，因此算法的總的復(fù)雜度為

O(N(nmr+mN(A)+Nsnm2+nmp+nmq))

如果降階系統(tǒng)的階m遠(yuǎn)遠(yuǎn)小于原始大規(guī)模系統(tǒng)的階n，且系統(tǒng)的輸入輸出個數(shù)p和q也遠(yuǎn)遠(yuǎn)小于n，此時共軛梯度法的計算復(fù)雜度為線性O(shè)(Nn)，其中N為迭代次數(shù)。

3 數(shù)值算例

在本節(jié)，我們測試比較了本文提出的共軛梯度法的有效性。

例1 考慮在區(qū)域Ω=(0,1)2上的熱傳導(dǎo)方程。熱傳導(dǎo)方程可以有如下形式

其中u=u(t,x,y)，(x,y)∈Ω，t∈[0,∞)。假設(shè)微分方程在空間域上等距剖分，格點(diǎn)數(shù)為d×d。導(dǎo)出的剛度矩陣A∈Rd2×d2是稀疏的、穩(wěn)定的，帶寬為d。系統(tǒng)的階為n=d2。假設(shè)b1∈Rn是一個所有元素都為1的向量。b2∈Rn是個隨機(jī)向量。假設(shè)B=[b1,b2]，C=BT。 此時，構(gòu)造的系統(tǒng) (A,B,C) 是個多輸入多輸出系統(tǒng)。

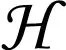
表1 2相對誤差比較

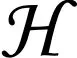
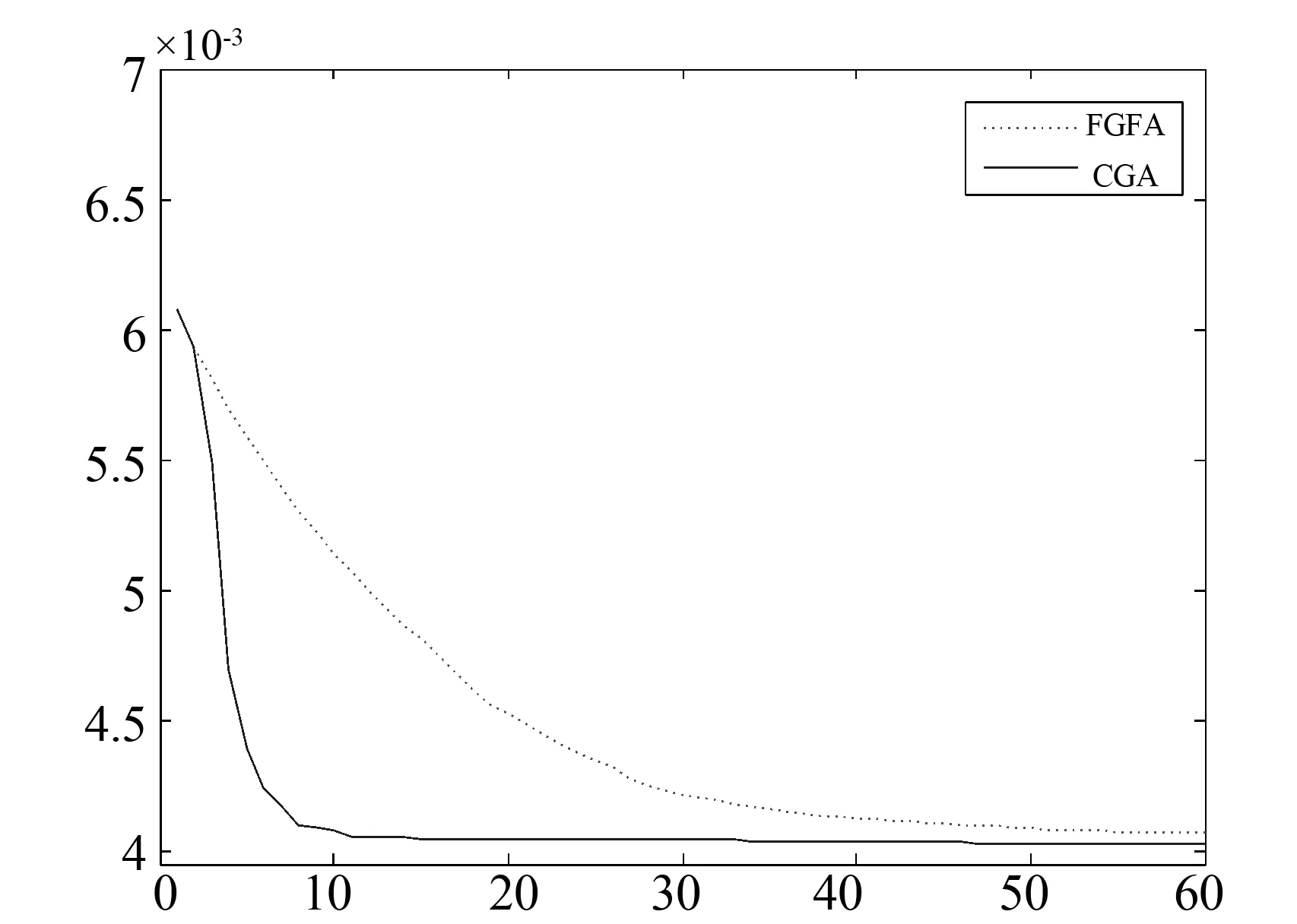
圖1 收斂曲線比較

4 總 結(jié)

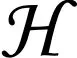
參考文獻(xiàn)：

[1]ANTOULAS A C. Approximation of large-scale dynamical systems [M]. Adv Des Control 6 SIAM, Philadelphia, 2005.

[2]GUGERCIN S, ANTOULAS A C. A survey of model reduction by balanced truncation and some new results [J]. International Journal of Control, 2004, 77(8): 748-766.

[3]HUANG X X, YAN W Y, TEO K. Linear-optimal model reduction [J]. IEEE Trans Automat Contr, 2001, 46: 1279-1284.

[4]HYLAND D C, BERNSTEIN D S. The optimal projection equations for model reduction and the relationships among the methods of wilson, skelton and moore [J]. IEEE Trans Automat Contr, 1985, 30: 1201-1211.

[5]LEPSCHY A, MIAN G A, PINATO G, et al. Rational approximation: a non-gradient algorithm [C]//Proc 30th IEEE CDC, 1991: 2321-2323.

[6]YAN W Y, LAM J. An approximate approach to optimal model reduction [J]. IEEE Trans Automat Contr, 1999, 44: 1341-1358.

[9]ZHOU K, DOYLE J C, GLOVER K. Robust and optimal control [M]. New Jersey: Prentice-Hall, 1996.

[10]ABSIL P A, MAHONY R, SEPULCHRE R. Optimization algorithms on matrix manifolds [M]. Princeton University Press, 2008.

[11]EDELMAN A, ARIAS T A, SMITHS T. The geometry of algorithms with orthogonality constraints [J]. SIAM J Matrix Anal Appl, 1999, 20: 303-353.

[12]VASILYEV D, WHITE J. A more reliable reduction algorithm for behavior model extraction [C]// Proc Int Conf on Computer， Aided Design (ICCAD), 2005: 812-819.