帶電小球在正交場中的運(yùn)動軌跡探討

黃尚鵬

(湖北省監(jiān)利縣朱河中學(xué),湖北監(jiān)利 433325)

問題.如圖1所示,范圍足夠大的磁感應(yīng)強(qiáng)度為B的勻強(qiáng)磁場,方向垂直 xOy平面向里,同時在 xOy平面內(nèi)充滿著勻強(qiáng)電場,方向豎直向上,質(zhì)量為 m、電荷量為 q的帶正電小球從坐標(biāo)原點出發(fā),沿 x軸正方向射入場區(qū),小球受電場力為自身重力的一半,試分析小球所有可能的運(yùn)動軌跡.若小球沿軸正方向射入場區(qū),小球的運(yùn)動軌跡又是怎樣的呢?

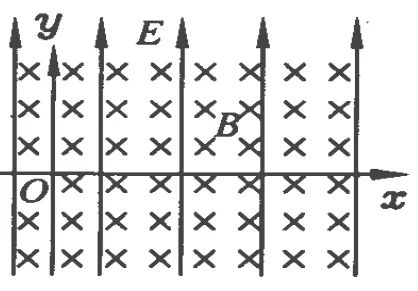
圖1

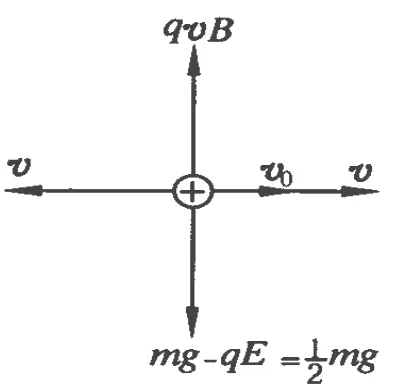
圖2

若小球沿x軸正方向射入場區(qū),如圖2所示,設(shè)小球的初速度為v0,小球受電場力和重力的合力為 mg-qE=方向豎直向下,沿 x軸正方向和負(fù)方向給小球兩個大小相等的輔助速度v,使 x軸正方向的速度所產(chǎn)生的洛倫茲力恰好與電場力和重力的合力平衡,即qvB=mg或?qū)懗蓈=,這樣我們可以將小球的運(yùn)動看成是由 x軸正方向的速度v引起的勻速直線運(yùn)動和由初速度v0及x軸負(fù)方向的速度v的合速度引起的勻速圓周運(yùn)動疊加而成的一種運(yùn)動.為此,我們建立一以速度v沿x軸正方向做勻速直線運(yùn)動的新坐標(biāo)系x′O′y′,初始時刻新坐標(biāo)系的原點在勻速圓周運(yùn)動軌跡的圓心處,下面我們可以通過坐標(biāo)變換求出小球的軌跡的參數(shù)方程.

當(dāng) 0≤v0＜v時,如圖 3所示,坐標(biāo)系 x′O′y′中勻速圓周運(yùn)動軌跡在x軸的下方,速度為 v-v0,方向為圓周運(yùn)動的逆時針方向,半徑 R=周期 T=角速度 ω=在坐標(biāo)系 x′O′y′中小球的坐標(biāo)為 x′=-Rsinω t,y′=Rcosω t,在坐標(biāo)系 xOy 中小球的坐標(biāo)為

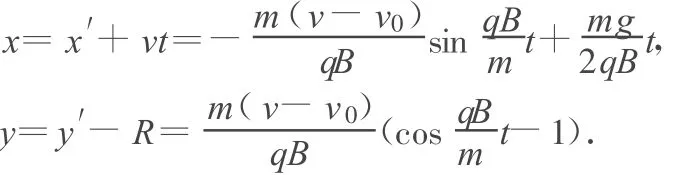
當(dāng) v0＞v時,如圖 4所示,坐標(biāo)系 x′O′y′中勻速圓周運(yùn)動軌跡在x軸的上方,速度為 v0-v,方向為逆時針方向,圓周運(yùn)動的半徑 R=顯然在坐標(biāo)系 x′O′y′中小球的坐標(biāo)為 x′=Rsinω t,y′=-Rcosω t,故在坐標(biāo)系 xOy中小球的坐標(biāo)為

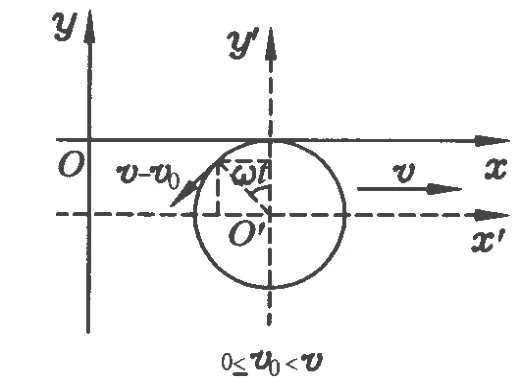
圖3

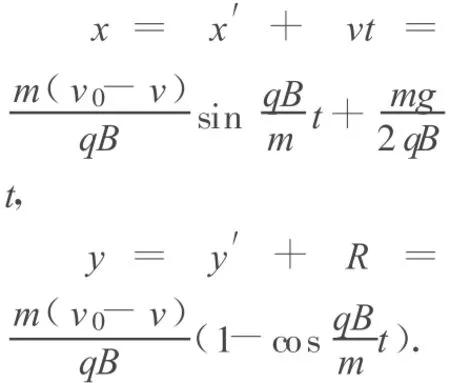
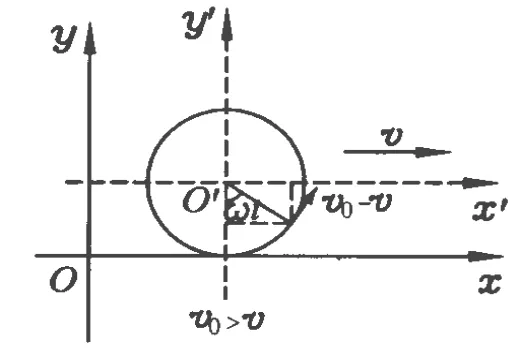
圖4

顯然上述兩種情況下小球軌跡的參數(shù)方程形式完全相同,特殊情況下,若v0=v,則小球受洛倫茲力恰好與電場力和重力的合力平衡,小球?qū)⒀?x軸正方向做勻速直線運(yùn)動.根據(jù)上述疊加思想可知,小球的運(yùn)動具有周期性且從初始時刻開始每經(jīng)過半個周期,小球運(yùn)動的水平位移Δx=與小球的初速度 v0的大小無關(guān).小球離開x軸的最大距離等于勻速圓周運(yùn)動的直徑,小球軌跡切線的斜率k=小球的速度方向沿軌跡的切線方向,下面我們分5種情況討論小球可能的運(yùn)動軌跡.

根據(jù)前面的討論可知,小球軌跡的參數(shù)方程可統(tǒng)一表達(dá)為如下形式

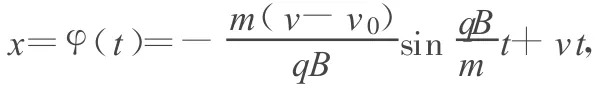
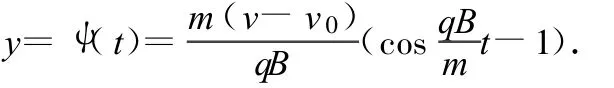
對 φ(t)和 ψ(t)求一階及二階導(dǎo)數(shù),有

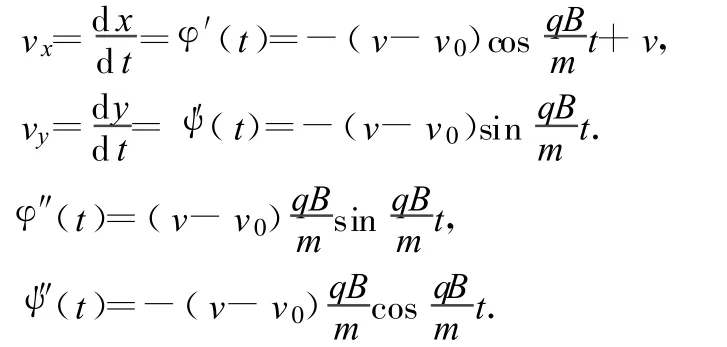
由參數(shù)方程所表示的函數(shù)的二階導(dǎo)數(shù)公式可知,

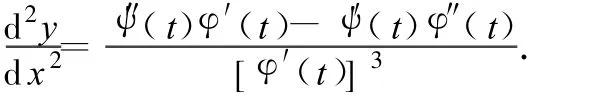
通過計算,可得

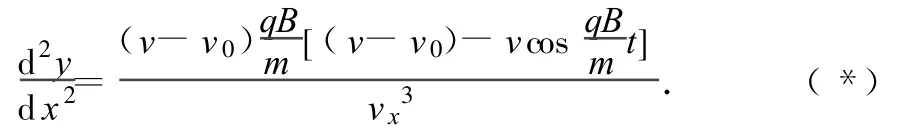
(1)當(dāng) v0=0時,由圖 3可知,小球在軌跡的最低點具有最大水平速度,最低點軌跡切線水平;小球在軌跡的最高點速度為零,軌跡切線的斜率不唯一或不存在,最高點不光滑出現(xiàn)尖點.這種情況除軌跡的最高點外,vx＞0,函數(shù)為凹函數(shù),軌跡向下凸.

(2)當(dāng)0＜v0＜v時,由圖 3可知,小球在軌跡的最低點速度水平向右,最低點軌跡切線水平;小球在軌跡的最高點也具有水平向右速度,最高點軌跡切線也水平.故這種情況軌跡可能存在拐點.

(3)當(dāng) v＜v0＜2v時,由圖4可知,小球在軌跡的最低點速度水平向右,最低點軌跡切線水平;小球在軌跡的最高點也具有水平向右速度,最高點軌跡切線也水平.故這種情況軌跡也可能存在拐點.

下面給出(2)、(3)兩種情況軌跡存在拐點的證明,并確定拐點的大致位置.

由高等數(shù)學(xué)知識可知,軌跡上某點是拐點的充要條件是該點的二階導(dǎo)數(shù)等于零,且該點附近兩側(cè)二階導(dǎo)數(shù)要改變符號.

當(dāng)0＜v0＜v時,vx＞0,令得 cosω t=1顯然有 0＜cosω t＜1,ω t是一、四象限的角,且由余弦函數(shù)的單調(diào)性可知,二階導(dǎo)數(shù)等于零的該點附近兩側(cè)二階導(dǎo)數(shù)要改變符號,故這種情況軌跡存在拐點,由圖3可知,拐點在軌跡的最高點和最低點的水平中心線的上方.考慮從初始時刻開始到第1次經(jīng)過最低點的過程,即0≤ω t≤π,由(*)式易知,在拐點的左側(cè),函數(shù)為凸函數(shù),軌跡向上凸;在拐點的右側(cè)函數(shù)為凹函數(shù),軌跡向下凸.

當(dāng) v＜v0＜2v時,vx＞0,令可得 cosω t=顯然有-1＜cosω t＜0,ω t是二、三象限的角,同理可知這種情況軌跡也存在拐點,由圖4可知,拐點也在軌跡的最高點和最低點的水平中心線的上方.考慮從初始時刻開始到第一次經(jīng)過最高點的過程,即0≤ω t≤π,由(*)式知,在拐點的左側(cè),函數(shù)為凹函數(shù),軌跡向下凸;在拐點的右側(cè),函數(shù)為凸函數(shù),軌跡向上凸.

(4)當(dāng) v0=2v時,由圖 4可知,小球在軌跡的最低點具有最大水平速度,最低點軌跡切線水平;小球在軌跡的最高點速度為零,軌跡切線的斜率k不唯一或不存在,最高點不光滑出現(xiàn)尖點.這種情況除軌跡的最高點外,vx＞0,函數(shù)為凹函數(shù),軌跡向下凸.

(5)當(dāng) v0＞2v時,由圖 4可知,小球在軌跡的最低點具有最大水平向右速度,最低點軌跡切線水平;小球在軌跡的最高點具有水平向左速度,最高點軌跡切線也水平,這種情況小球在水平方向時而向右運(yùn)動,時而向左運(yùn)動,在軌跡的最高點下方存在水平分速度為零而豎直分速度不為零的點,在這些點軌跡的切線沿豎直方向.由(*)式知,當(dāng) vx＞0時,函數(shù)為凹函數(shù),軌跡向下凸;當(dāng) vx＜0時函數(shù)為凸函數(shù),軌跡向上凸.

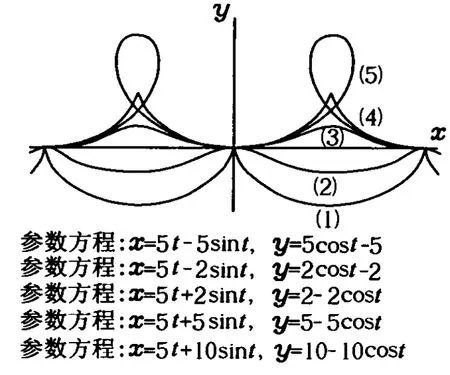
圖5

采用函數(shù)作圖軟件SmartGraph作出的上述5種情況下小球的運(yùn)動軌跡如圖5所示,圖中 m=1 kg,q=1 C,B=1 T,v=5 m/s.各圖線代表的初速度分別為:

(1)v0=0;(2)0＜v0＜v,v0=3 m/s;(3)v＜v0＜2v,v0=7 m/s;(4)v0=2v=10 m/s;(5)v0＞2v,v0=15 m/s.注意小球的實際運(yùn)動軌跡在y軸的右側(cè),由圖5可知,軌跡的形狀與上述分析是一致的.

至此,當(dāng)小球沿 x軸正方向射入場區(qū)時,小球所有可能的運(yùn)動軌跡都已解決,那么當(dāng)小球沿y軸正方向射入場區(qū)時,小球的運(yùn)動軌跡又是怎樣的呢?這種情況要比上述情況要簡單些,可能的軌跡形狀只有一種,請看如下分析.

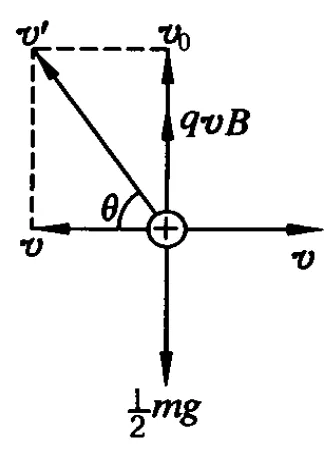
圖6

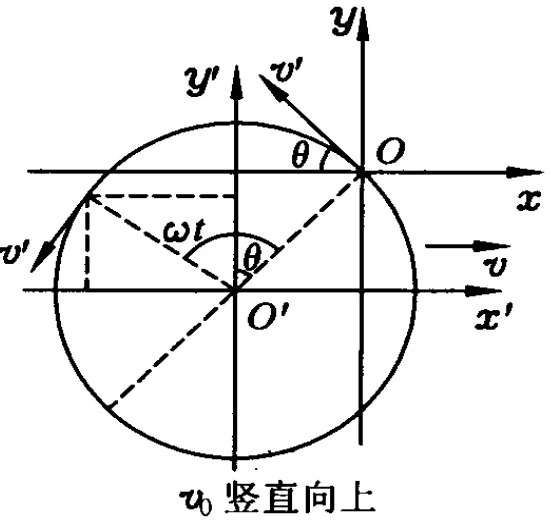
圖7

若小球沿y軸正方向射入場區(qū),如圖6所示,同樣將小球的運(yùn)動看成是由 x軸正方向的速度v引起的勻速直線運(yùn)動和由初速度v0及 x軸負(fù)方向的速度v的合速度v′引起的勻速圓周運(yùn)動疊加而成的一種運(yùn)動.如圖7所示,坐標(biāo)系 x′O′y′中勻速圓周運(yùn)動的速度 v′=方向為逆時針方向,初始時刻 v′與x軸負(fù)方向的夾角為θ,且 tanθ=圓周運(yùn)動的半徑 R=顯然在坐標(biāo)系 x′O′y′中小球的坐標(biāo)為 x′=-Rsin(ω t-θ),y′=Rcos(ω t-θ),故在坐標(biāo)系 xOy中小球的坐標(biāo)為

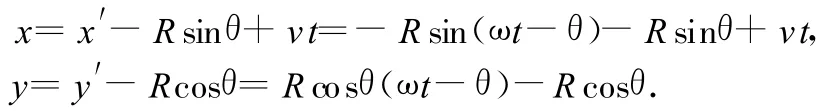
由于初速度豎直向上,故初始時刻軌跡的切線沿豎直方向,由圖7可知,小球在軌跡的最高點具有水平向左速度,最高點軌跡切線水平;當(dāng)小球再次回到軸時,小球的速度豎直向下,軌跡的切線沿豎直方向;小球在軌跡的最低點具有最大水平向右速度,最低點軌跡切線水平.這種情況小球在水平方向時而向左運(yùn)動,時而向右運(yùn)動.從初始時刻開始每經(jīng)過一個周期,小球運(yùn)動的水平位移為Δx=vT=與小球的初速度大小無關(guān).

仿造前面的方法,類似可得

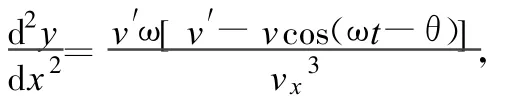
故當(dāng) vx＜0時,,函數(shù)為凸函數(shù),軌跡向上凸;當(dāng) vx＞0時函數(shù)為凹函數(shù),軌跡向下凸.

采用函數(shù)作圖軟件SmartGraph作出的這種情況下,小球的運(yùn)動軌跡如圖8所示,圖中m=1 kg,q=1 C,B=1 T,v=5 m/s.相應(yīng)的圖線所對應(yīng)的初速度分別為:(6)v0=5 m/s;(7)v0=12 m/s.

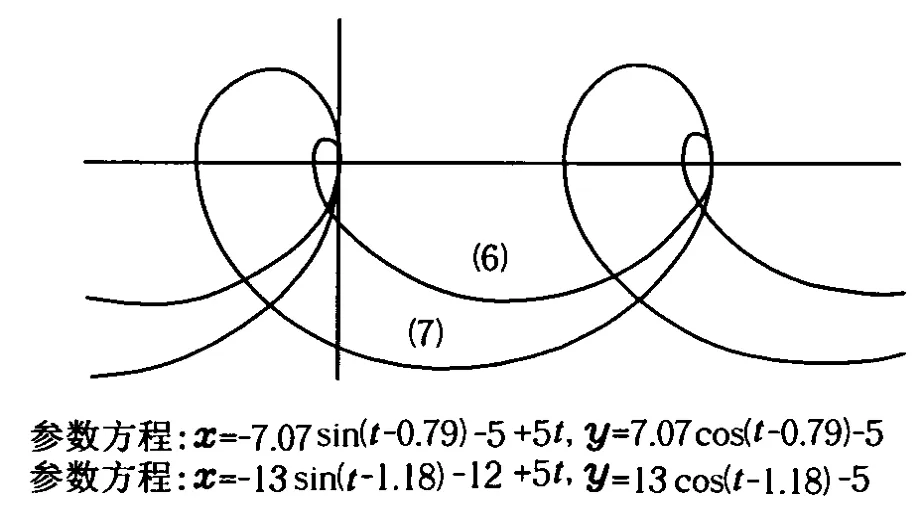
圖8

編者按:帶電粒子在正交場中的運(yùn)動,本刊已發(fā)表了多篇文章.如無更新和更深入的意見,本刊將不再發(fā)表該類文章.