賦值法在高中物理教學中的應用

劉益民

(揚州市寶應縣中學,江蘇寶應 225800)

賦值法解題,就是對題中的某些參量賦予一定的值,以便于研究和計算得出正確結果的一種解題方法.賦值法在解題應用中屬于一種巧解,但是賦值法在物理概念教學、規律教學、習題教學、實驗教學多方面都有著廣泛的應用.

1 應用于物理概念教學中,化深奧為淺顯

高中物理與初中物理顯著的區別之一就是物理概念多用物理表達式而少用文字與數據,許多學生特別是高一學生一開始都不是很適應,其實我們可以借助于賦值法,讓學生逐步學習與理解物理概念.

例1.小明同學以 v1的速度勻速向東運動,感覺風從正北方向以速度v2向他吹來,則此時的風速大小與方向?

解析:為了解決這一相對速度問題,在教學過程中筆者采用了賦值法設置幾個問題.

(1)小明同學以6 m/s的速度勻速向東運動,感覺不到風,則風速為6 m/s,向東;

(2)小明同學以6 m/s的速度勻速向東運動,感覺風以6 m/s迎面吹來,則風速為 0;

(3)小明同學以6 m/s的速度勻速向東運動,感覺風以4 m/s迎面吹來,則風速為 2 m/s,向東;

(4)小明同學以6 m/s的速度勻速向東運動,感覺風以8 m/s迎面吹來,則風速為 2 m/s,向西;

(5)小明同學以6 m/s的速度勻速向東運動,感覺風以8 m/s從正北方向吹來,則風速為10 m/s,北偏東53°.

通過層層設問,最終學生很容易地得出人對地、風對地、風對人3個速度之間的關系(如圖1所示)為 v風地=v風人+v人地,解決題中的問題將輕而易舉.

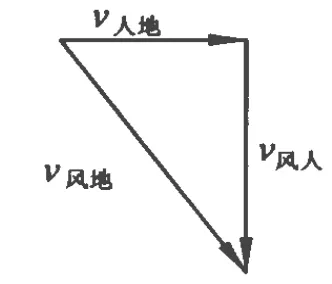
圖1

小結:本題也可以用運動的分解來分析,即風速向東的分速度與人速相同,然后再根據速度的合成得風速大小方向為東偏南tanα=.而通過賦值法會讓學生在數值的討論中經歷探究過程,然后輕松地發現較難理解與掌握的速度運算法則,得出絕對速度、牽連速度、相對速度三者之間的一般意義下的關系式為 vAC=vAB+vBC,這對學生以后處理類似問題會很有幫助.

2 應用于物理規律教學中,化抽象為直觀

高中物理規律中有的理解要求較高,而且抽象空洞,如果我們局限于公式的推導與證明,學生更會感到迷茫與難學,不妨用賦值法降低接受難度,讓規律先清晰明了起來再來學習.

例2.劈尖干涉是一種薄膜干涉,其裝置如圖2所示.將一塊平板玻璃放置在另一平板玻璃之上,在一端夾入兩張紙片,從而在兩玻璃表面之間形成一個劈形空氣薄膜.當光垂直入射后,從上往下看到的干涉條紋如圖3所示.干涉條紋有如下特點:(1)任意一條明條紋或暗條紋所在位置下面的薄膜厚度相等;(2)任意相鄰明條紋或暗條紋所對應的薄膜厚度差恒定.現若在圖2裝置中抽去一張紙片,則當光垂直入射到新的劈形空氣薄膜后,從上往下觀察到的干涉條紋

(A)變疏. (B)變密. (C)不變. (D)消失.

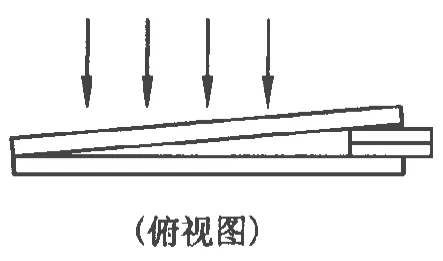
圖2

圖3

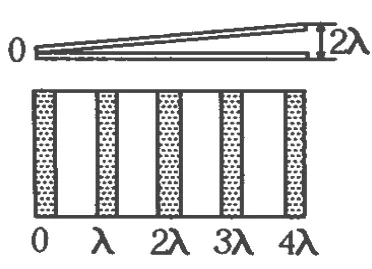
圖4

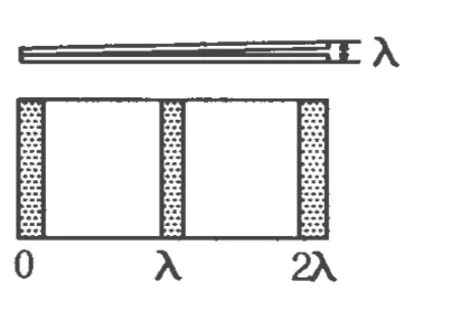
圖5

解析:楔形空氣層的上下兩個表面反射的兩列光波發生干涉,空氣層厚度相同的地方,兩列波的路程差相同,故如果被測表面是平的,干涉條紋就是一組平行的直線.而抽去一張紙片對干涉條紋疏密的影響直接影響的是最大光程差,影響了干涉條件的總條數,最終影響到了條紋的疏密.為了對這一影響有一個直觀的認識,我們可以采用賦值法進行教學.如圖4所示,可設每張紙的厚度為一個波長,即最大光程差就會為4λ,最終我們就會在上表面觀看到5條條紋(此處由于半波損失的問題,在高中物理課堂教學中也不宜涉及,因此可含糊說明),而當抽去一張紙時,最大光程差變成2λ,如圖5所示,因此只能觀察到 3條條紋,因此條紋變疏,選(A).

拓展:如果將上面一塊平板玻璃向上移的過程中,請問你會觀察到什么現象?

剖析:現在已經涉及到光的薄膜干涉條件變化問題,同樣我們可以使用賦值法進行分析,如圖6所示,假設向上移兩張紙的厚度,即 2λ的距離,這樣對應于剛才最右端的最大光程差4λ的條紋將會移動到最左邊,而右側最大光程差也相應變成了8λ,因此仍然看到的是5條條紋,條紋的疏密仍然不變,但是在上抬過程中,干涉條紋向左側在不斷移動.

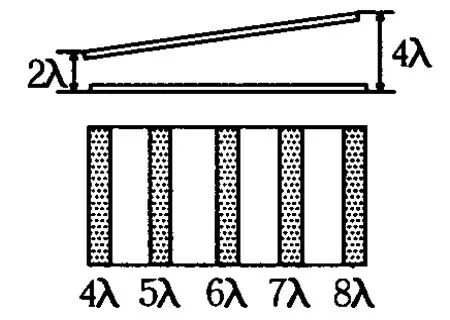
圖6

小結:薄膜干涉又稱為等厚干涉,可以試著引導學生分析推導相鄰的條紋間距公式,即Δx=其中 L為平板玻璃的寬度,d為劈形空氣薄膜的最大厚度,d減小時,Δx會增大.或者分析推導對應劈尖的傾角正弦值sinθ=Δx是增大時,sinθ會減小.但是這些理論上的分析過于數學化,也無形中增加了學生學習的負擔,而通過賦值法在數字面前,學生感性認識較差的劈尖干涉將會呈現在眼前,其中的變化也會變得如此直觀,結論也將不言而喻.因此,賦值法并非簡單的投機取巧,而是在那些簡單的數字之間蘊藏著深刻的物理原理.

3 應用于物理習題教學中,化復雜為簡單

在高中物理的習題中,特別是求某個物理量與其他物理量的關系或變化規律的選擇題,有時若采用常規解法繁瑣、費時,若用賦值法,只要將其中相關的不確定物理量取一定的值,代入式中得出對應值下的解,即可確定正確的選項,有時甚至一眼就能看出答案,就能達到快速準確的目的.

例3.如圖7所示,沿豎直桿以速度 v勻速下滑的物體A通過輕質細繩拉光滑水平面上的物體B,細繩與豎直桿間的夾角為θ,則以下說法正確的是

(A)物體B向右勻速運動.

(B)物體B向右勻加速運動.

(C)細繩對 A的拉力逐漸變小.

(D)細繩對B的拉力逐漸變大.

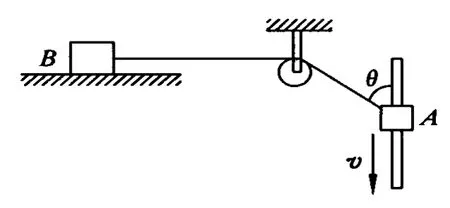
圖7

解析:物體 A沿繩的分速度與物體B運動的速度大小相等,有 vB=vcosθ,隨物體 A 下滑,θ角減小,vB增加,但不是均勻增加,θ越小,cosθ增加越慢,vB增加越慢,也即B的加速度越來越小,由 T=mBaB可知,細繩的拉力逐漸變小,故只有(C)正確.

拓展剖析:假設A物體由與B等高處勻速下滑,即sA=vt,設輪與桿垂直距離為 L,則B物體的位移大小為sB=判斷B向右是否是勻速運動只需要看sB-t圖線是否為線性函數,明顯不是,而B向右是否做勻加速直線,只需要作圖是否為線性函數,結果也不是勻加速運動,那么加速度如何變化,可根據ˉv=由于時間取值相同而且較短,可作出ΔsB-t即ˉv-t圖線,可看出B的運動是向右做加速度減小的加速運動.如圖8所示,這些圖線可以利用Excel軟件采用“賦值法”很快得出,因此選(C).

圖8

小結:本題判斷B物體的加速度變化是一難點.由數學導數知識可知速度應該是位移的一階導數,vB=sB′=其為非線性函數,則 B必做變加速直線運動,而加速度又應是位移的二階導數,即 aB=sB″=最終數學解析式復雜無比,物理意蘊所剩無幾,從中得出 aB↓=sB″↓=可能有點難,也有點過,也就是說在對付選擇題時用此法可謂“殺雞用牛刀”了.而使用賦值法不僅直觀易懂,而且及時滲透探究方法的教學,也將復雜的物理規律變得如此簡單.

4 應用于物理實驗教學中,化理性為感性

在高中物理實驗中,選擇器材是學生最感頭痛的,選擇電學參數大的好還是小的好我們往往左右為難,此時真正采用賦值法,取大或取小試一試,做一做,就能見分曉.

例4.實驗室內有一電壓表,量程為5 V,內阻約為2.5 kΩ.現要測量其內阻,實驗室提供如下器材:

電源 E1(電動勢為3 V,內阻不計),電源 E2(電動勢6 V,內阻不計),電阻箱 R(0～9 999 Ω),滑線變阻器 R1(總阻值約15 Ω,額定電流1 A),滑線變阻器 R2(總阻值約150 Ω,額定電流1 A),開關S及導線若干.

在既不損壞儀器又能使精確度盡可能高的條件下,請你根據提供的器材,設計一個測量電壓表內阻的電路.(1)請畫出你所設計的電路圖;(2)用你設計的電路測量出的電壓表內阻將________真實值(填等于、小于或大于);(3)在你設計的電路中,電源應選_______,滑線變阻器應選________.

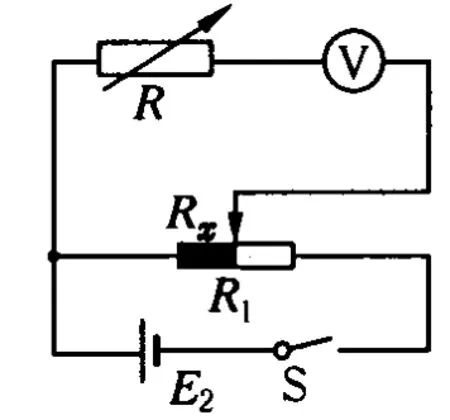
圖9

解析:設計的電路圖如圖9所示,設計實驗原理是使用半偏法測量電壓表內阻,先按圖接線,圖中 R為電阻箱,合下S,調節R=0,再調節 R1使電壓表指針滿偏;然后保持變阻器電阻Rx不變,調節 R使電壓表指針半偏,記下R的值,則有 RV=R.

而這種半偏法同時存在著明顯的系統誤差,因為先使電壓表指針滿偏,再調節 R時必將增大并聯電阻,促使左側并聯電路分得電壓略高于電壓表滿偏電壓,當先調節R使其半偏時,則電阻箱R分得電壓必將超過一半,由分壓原理可知,其R的阻值此時要略大于電壓表內阻,因此用此時電阻箱阻值替代電壓表內阻要偏大,則測量值要大于真實值.

因此,RV=R的附加條件是恒壓,即 RV?Rx,Rx是使電壓表滿偏時的滑線變阻器接入的電阻,這使得滑線變阻器阻值本身就需要小,而且只有電源電動勢越大才能使電壓表滿偏時的滑線變阻器接入的電阻越小.對這兩點多數學生缺少感性認識.我們可以通過演示實驗,結合實物電路進行說明,如圖10所示,其中對兩器材的選擇可采用“賦值法”進行演示.如電源電壓取18 V與取3 V比較,滑線變阻器取150 Ω與取25 Ω進行比對,可發現大電動勢加小滑線變阻器可保證 Rx取值較小,確保“恒壓”,這樣造成的系統誤差也就越小.

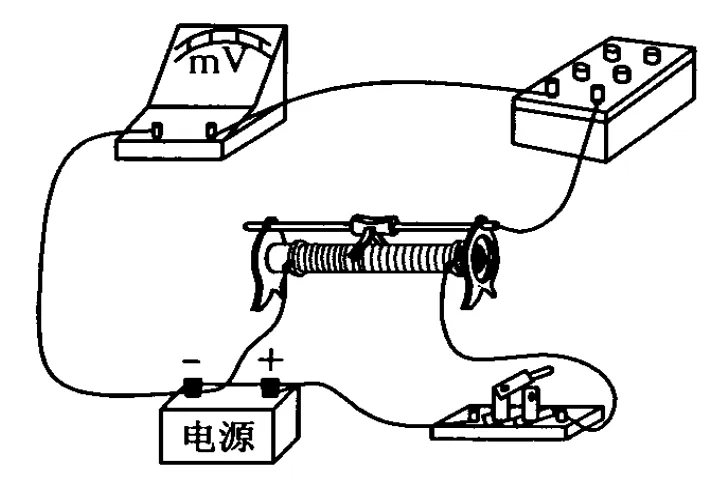
圖10

小結:此實驗為恒壓半偏法,同樣存在著系統誤差,只有正確分析產生誤差的原因及實驗結論成立的近似條件,才能知道如何選擇電源及滑線變阻器,通過實驗器材演示及真實的賦值過程,學生將會對實驗原理有透徹的理解與感悟.

總之,賦值法在處理高中物理中一些疑難問題時有它獨到的優點,它能讓我們通過數據來透視物理現象,感受物理變化,體驗數字探究的思維方法.但是在應用賦值法時要注意賦值的合理性,對于物理條件所制約的物理量的取值要慎重,不可任取.同時對于物理解析方程的單調性質也有一定要求,可以應用賦值法的物理方程一般必須為單調函數,否則課堂上簡單地取幾個值就去下結論肯定會導致極其荒謬的錯誤.