中考數學交流型試題歸類解析

221700 江蘇豐縣中學 張 啟

新課標提出“能用數學語言表達問題、展開交流，形成用數學的意識，學會與他人合作”，將“數學交流”貫穿在整個知識領域中.可見，數學交流已經是數學教學改革的一種潮流，在近幾年的中考中，“數學交流”型試題備受命題者青睞，已成為中考命題的新趨勢.這類問題通常給出一段閱讀材料，然后提出問題，通過交流材料的內容，從中獲取有用的信息，在理解的基礎上結合已有知識來解決問題.現以2011年中考試題為例就交流的條件、結論、概念、方法等形式加以歸類說明.

1 交流條件

這類問題通常是在一致的結論下，交流結論成立的條件或結論成立更為一般性的條件.解此類問題的基本策略是執果索因，從結論及部分條件出發，結合所學及與結論相關的知識，從中找到滿足結論的條件.

例1(2011年泉州)某班將舉行“慶祝建黨90周年知識競賽”活動，班長安排小明購買獎品，下面兩圖是小明買回獎品時與班長的對話情境：

小明：買了兩種不同的筆記本共40本，單價分別為5元和8元，我領了300元，現在找回68元.

班長：你肯定搞錯了!

小明：噢!我把自己口袋里的13元一起當作找回的錢款了.

班長：這就對了!

請根據上面的信息，解決問題：

試計算兩種筆記本各買了多少本?

請你解釋：小明為什么不可能找回68元?

解 (1)解法1設5元，8元的筆記本分別買x本，y本，

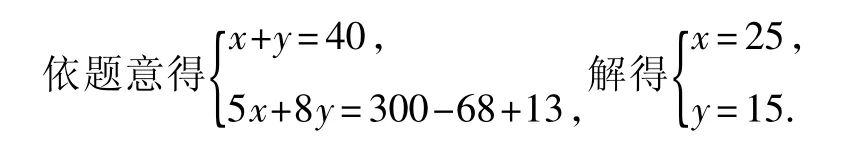
答：5元和8元筆記本分別買了25本和15本.

解法1應找回的錢款為300-5×25-8×15=55≠68，故不能找回68元，

解法2設買m本5元的筆記本，則買(40-m)本8元的筆記本，

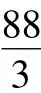
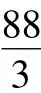
解法3買25本5元的筆記本和15本8元的筆記本的價錢總數應為奇數而不是偶數，

故不能找回68元.

2 交流結論

這類試題往往是雖然條件發生了變化，但問題本質特征并未發生變化.解決這類問題，須從所給條件出發，通過分析、比較、確立結論，或讓你判斷所給的結論是否正確，再進行說明.

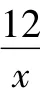
(1)試用列表或畫樹狀圖的方法列舉出所有點P(m，n)的情形;

(2)分別求出點P(m，n)在兩個反比例函數的圖象上的概率，并說明誰的觀點正確.

解(1)列表如下：

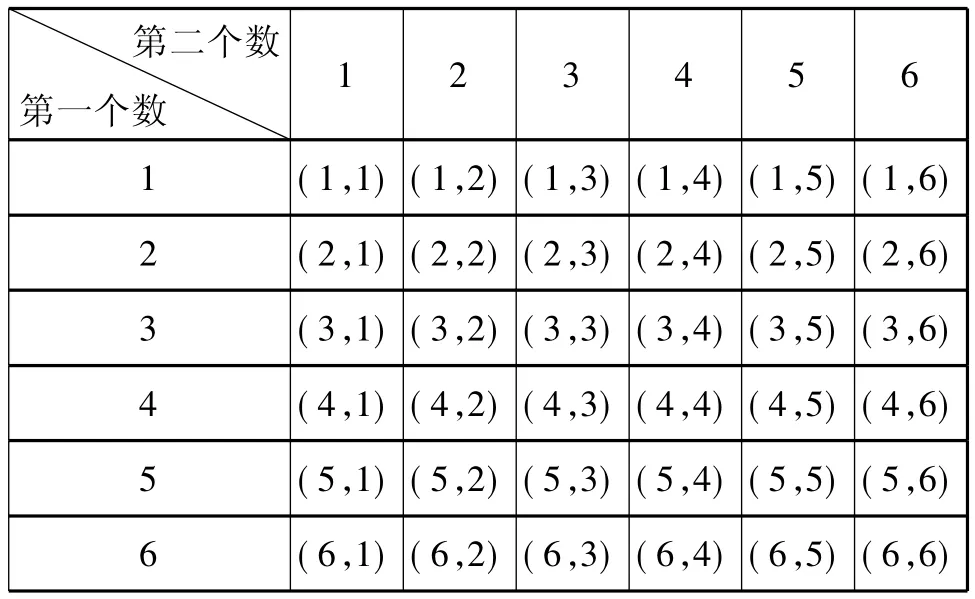
第二個數第一個數1 2 3 4 5 6 1 (1，1)(1，2)(1，3)(1，4)(1，5)(1，6)2 (2，1)(2，2)(2，3)(2，4)(2，5)(2，6)3 (3，1)(3，2)(3，3)(3，4)(3，5)(3，6)4 (4，1)(4，2)(4，3)(4，4)(4，5)(4，6)5 (5，1)(5，2)(5，3)(5，4)(5，5)(5，6)6 (6，1)(6，2)(6，3)(6，4)(6，5)(6，6)

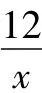
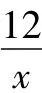
3 交流概念

這類試題通常是把一些新概念類似地運用到其它的圖形或對象上，雖然對象變化了，但某些性質可遷移到這一對象上，然后提出與這個概念密切相關的問題要求我們去解決.

例3(2011年江西)某課題學習小組在一次活動中對三角形的內接正方形的有關問題進行了探討：

定義：如果一個正方形的四個頂點都在一個三角形的邊上，那么我們就把這個正方形叫做三角形的內接正方形.

結論：在探討過程中，有三位同學得出如下結果：

甲同學：在鈍角、直角、不等邊銳角三角形中分別存在________個、________個、________個大小不同的內接正方形.

乙同學：在直角三角形中，兩個頂點都在斜邊上的內接正方形的面積較大.

丙同學：在不等邊銳角三角形中，兩個頂點都在較大邊上的內接正方形的面積反而較小.

任務：(1)填充甲同學結論中的數據;

(2)乙同學的結果正確嗎?若不正確，請舉出一個反例并通過計算給予說明，若正確，請給出證明;

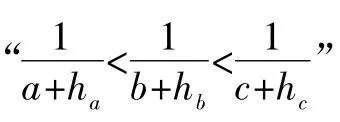
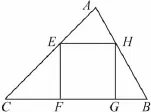
圖1

解(1)1，2，3.

(2)乙同學的結果不正確.

例如：在 Rt△ABC中，∠B=90°，

AB=BC=1，則AC=.

如圖2，四邊形DEFB是只有一個頂點在斜邊上的內接正方形.設它的邊長為a，則依題意可得

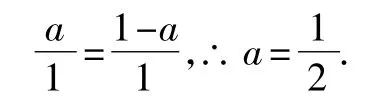
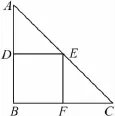
圖2

如圖3，四邊形DEFH兩個頂點都在斜邊上的內接正方形.設它的邊長為b，則依題意可得

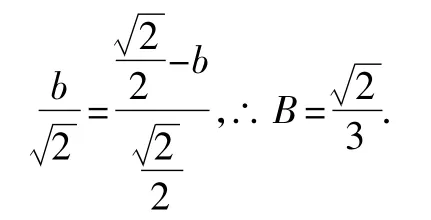
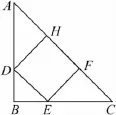
圖3

∴a＞b.

(3)丙同學的結論正確.

設△ABC的三條邊分別為a，b，c，不妨設a＞b＞c，三條邊上的對應高分別為ha，hb，hc，內接正方形的邊長分別為xa，xb，xc.

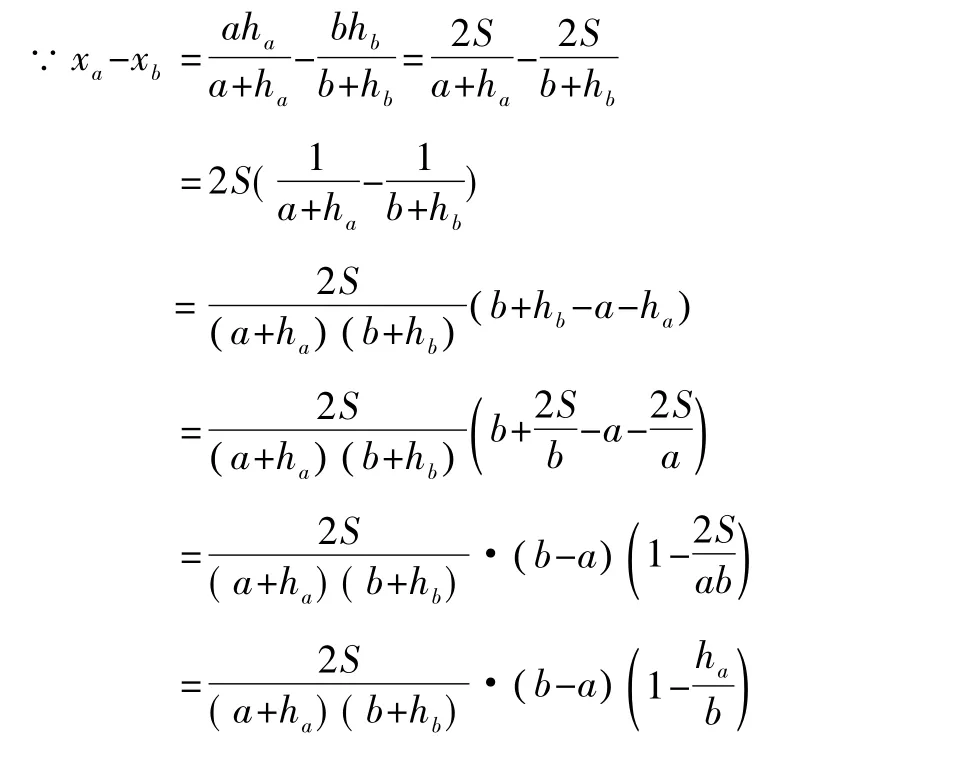
∴x＜x，即x2＜x2.abab

∴在不等邊銳角三角形中，兩個頂點都在較大邊上的內接正方形的面積反而較小.

點評本題定義了新概念“內接正方形”，解決問題的關鍵是深刻理解閱讀材料所提供的新概念，充分挖掘新概念的內涵和本質，并能夠運用所學過的知識對新概念作出合理的解釋，進而將陌生的概念轉化為熟悉的知識去理解，在此基礎上結合已有的知識加以解決.

4 交流方法

這類試題往往是對于一個新問題，雖然問題的條件和結論都比較陌生，但可通過討論交流得到解決問題的方法.解決此類問題的關鍵是認真閱讀其內容，理解其實質，把握其方法、規律，然后提出一個類似或在此基礎上有所拓展的問題，要求學生用類比的方法加以解決.

例4(2011年紹興)數學課上，李老師出示了如下的題目.

在等邊三角形ABC中，點E在AB上，點D在CB的延長線上，且ED=EC，如圖4.試確定線段AE與DB的大小關系，并說明理由.

小敏與同桌小聰討論后，進行了如下解答：

(1)特殊情況，探索結論

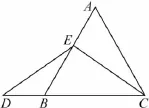
圖4

當點E為AB的中點時，如圖5，確定線段AE與DB的大小關系，請你直接寫出結論：

AE______DB(填“＞”，“＜”或“=”).

(2)特例啟發，解答題目

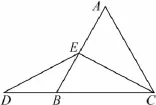
圖5

解題目中，AE與DB的大小關系是：AE______DB(填“＞”，“＜”或“=”).理由如下：如圖6，過點E作EF∥BC，交AC于點F.

(請你完成以下解答過程)

(3)拓展結論，設計新題

在等邊三角形ABC中，點E在直線AB上，點D在直線BC上，且ED=EC.若△ABC的邊長為1，AE=2，求CD的長(請你直接寫出結果).

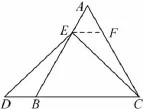
圖6

解(1)=.

(2)=.

方法1如圖6，等邊三角形ABC中，

∠ABC=∠ACB=∠BAC=60°，AB=BC=AC，

∵EF∥BC，

∴ ∠AEF=∠AFE=60°=∠BAC，

∴△AEF是等邊三角形，

∴AE=AF=EF，

∴AB-AE=AC-AF，即BE=CF，

又∵ ∠ABC=∠EDB+∠BED=60°，∠ACB=∠ECB+∠FCE=60°，

∴ ∠EDB+∠BED=∠ECB+∠FCE.

∵ED=EC，

∴∠EDB=∠ECB，

∴∠BED=∠FCE，

∴ △DBE≌△EFC，∴DB=EF，AE=BD.

方法2在等邊三角形ABC中，

∠EDB+∠BED=∠ECB+∠ACE=60°

∵ED=EC，∴ ∠EDB=∠ECB，

∴∠BED=∠ACE.

∵EF∥BC，∴ ∠AEF=∠AFE=60°=∠BAC，

即△AEF是正三角形，∠EFC=180°-∠ACB=120°=∠ABD，

∴ △EFC≌△DBE，∴DB=EF，

而由△AEF是正三角形可得EF=AE.

∴AE=DB.

(3)1或3.

點評解決這類問題首先要仔細閱讀材料，認真研究范例的解答過程，然后運用類比的方法，結合所學知識靈活解答.

從以上問題中可以看出，這類問題的特征就是通過學生的交流來表明他們對這個問題的理解和認識，同時讓應試者參與討論，并把一些觀點與數學表達符號化，讓學生運用不同的數學表達，以此來考查學生的數學意識和數學知識.通過中考試題中出現的交流問題，要求學生在今后的學習中，要學會通過一定的問題情景，自主地去探索問題，能較清楚地表達和交流解決問題的過程和結果，以培養觀察、發現、分析和歸納的能力.