立體圖形課件制作中的數學分析與技術手段
430062 湖北大學數學與計算機科學學院 朱 慧
430070 湖北省實驗幼兒師范學校 劉 欣
立體圖形課件制作中的數學分析與技術手段
430062 湖北大學數學與計算機科學學院 朱 慧
430070 湖北省實驗幼兒師范學校 劉 欣
人們很早就認識到圖形語言具有特殊作用,從不同的角度、不同的方向觀看圖形時就會產生不同的視覺效果,圖形也就有了文字所不能及的優越性.俗話說得好:“靈感產生于多維度的觀察與思考.”初中時期,學生們就曾遨游在三視圖的空間里,從正面、側面和俯視面三個維度觀察圖形,全面地認識事物,在認知的過程中培養和發展了的空間想象能力.
利用現代信息技術,例如幾何畫板,鮮活地呈現視圖的過程,則更有助于激發學生的學習興趣,提高教學效果,有步驟地培養學生的空間想象能力.本文僅就三視圖課件中正四棱錐的制作來說明如何利用幾何畫板軟件中的【動畫】和【移動】命令制作動態旋轉的正四棱錐和它的三種視圖動畫,以及制作過程中的數學思考與技術手段.
【動畫】是運動形式,有兩種呈現方式:手動動畫和自動動畫.自動動畫又可以分為有規則的運動和無規則的運動(俗稱“亂動”).對于無規則的運動,我們不研究它,而其他兩種,幾何畫板都可以滿足我們的需求.
幾何畫板軟件中的【動畫】和【移動】命令是在【編輯】菜單下的【操作類按鈕】中,通過【動畫】和【移動】命令制作出具有“動畫”功能的按鈕,再通過這個按鈕對移動對象進行操作和控制.例如,當我們在工作區中選中圓上的點A,再點擊【編輯】/【操作類按鈕】/【動畫】,打開【動畫屬性】對話框,根據需要選擇適當的方向、次數和速度,單擊【確定】后,在工作區中生成一個【動畫點】按鈕(如圖1).單擊該按鈕時,點A在圓上運動.再單擊停止運動.
例 制作正四棱錐的三視圖的動畫.
本課件制作的意圖就是將正四棱錐以空間形式動態地展示出各個面,并多角度的觀察圖形,用動畫演變得到正視圖、左視圖、俯視圖(如圖2).
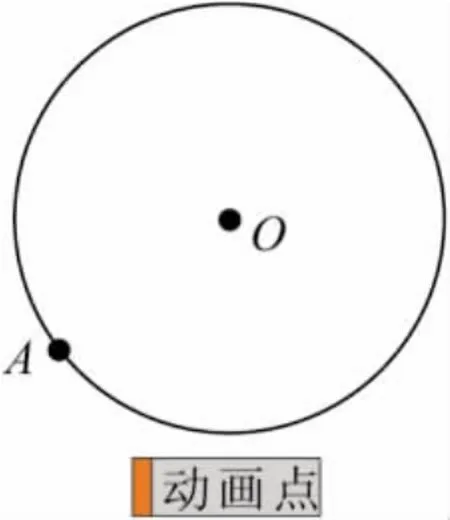
圖1

圖2 正四棱錐的三視圖
在作圖之前先了解一下基本信息:
(1)正四棱錐有五個面:四個側面和一個底面,四個側面都是等腰三角形,底面是一個正方形,并且正方形的四個頂點共圓.在畫法幾何中,將立體圖形平面化,底面正方形的四個頂點是在某一橢圓上,正四棱錐的頂點在過底面正方形的中心且垂直于底面的直線上.
(2)制作動畫要確定動畫的對象、動畫對象的運動軌跡.
(在具體做動畫前必須先畫出正四棱錐,畫法步驟詳見后面附錄)
1 轉動的正四棱錐(自動動畫)
分析 如圖3,目前呈現在前面的是△SAB,想要將其他面的三角形依次在正前方出現,顯然點S是不動的,只需將底面的四個頂點旋轉相應的角度,并且旋轉過程中,點與點之間的位置關系不變,均是繞著直線SO轉動的,那么它們之間應相互關聯.如何關聯?四個頂點是由點Q經過迭代得來的,因此四個頂點是受點Q牽制的.可以以點O為旋轉中心將點Q繞逆時針方向沿著圓旋轉360°(或大于360°),則四棱錐所有面就依次在正前方呈現.動畫的對象就是點Q,動畫的軌跡就是圓O.但這里的旋轉只是將正四棱錐繞底面旋轉,如同將四棱錐放在平面上旋轉,美中不足的是底面不能轉過來.如何才能轉動底面呢?再來看圖3,轉動底面,即是轉動底面的橢圓,在作橢圓過程中,點P是任取的點,由它才有了直線PO和之后的一系列動作,因此點P是最原始的關鍵點,可以轉動點P使整個四棱錐包括橢圓在空間內運動.
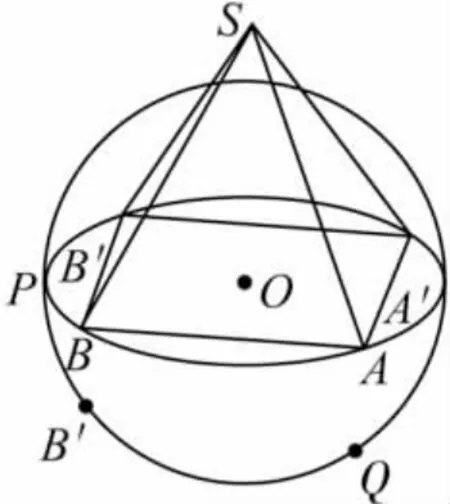
圖3
具體的作法如下:
隨著網絡信息技術的普及,學術期刊的發展環境迎來了極大的變化與挑戰。作為分享科研信息和學術交流的陣地,科技期刊的生存方式也發生了根本性的變化。新媒體的出現,多種多樣的傳播方式使得科研成果的生產加工和轉化發生了改變。雖然是科技期刊,應該走在科技前端,但由于期刊品牌在市場上沒有知名度和影響力,在收發稿件上很落后,作者和審稿專家隊伍也很難擴大范圍。對于很多互聯網同步不及時的地方科技期刊,期刊品牌影響力不夠,知名度也小,許多優秀稿件無處可投,同時稿件的外審工作繁雜,這顯然阻礙了科研成果的展示和交流。
(1)作出正四棱錐,如圖5所示.(可以將△SAB填充顏色,試圖效果更直觀)
(2)制作動畫按鈕【水平轉動】.選中點Q,點擊【編輯】菜單中的【操作類按鈕】/【動畫】,在彈出的對話框中選擇適當的方向、次數和速度,按【確定】即可在畫布上出現【動畫點】按鈕.右鍵單擊【動畫點】/【屬性】/【標簽】,將“動畫點”名稱改為“水平轉動”.單擊【水平轉動】,正四棱錐隨著點Q的運動而以直線SO為軸在平面內旋轉,再點擊則停止旋轉.
(3)制作動畫按鈕【底面翻轉】.選中點P,操作同上.右鍵單擊【動畫點】/【屬性】/【標簽】,將“動畫點”名稱改為“底面翻轉”.單擊【底面翻轉】,正四棱錐隨著點P的運動而在空間內旋轉,再點擊則停止旋轉.
2 主視圖(手動動畫)
分析 主視圖是從正面內得到由前向后觀察物體的視圖,特點是正四棱錐的頂點位置不變,底面的中心也不變,只是底面正方形在正視圖中縮成一條等邊長的水平線段.
易知使底面正方形縮成一條線段,則相應的橢圓也成為一條線段,點Q,A,A'三點重合,故可以以點A為動畫對象,使點A移動到點A'即可.
作法 選中點A不放,將點A移動到點A',得到如圖4,此時就是該四棱錐的正視圖,再點擊畫布上的【水平轉動】按鈕,則正四棱錐水平放置的各種形式的正視圖都可以呈現出來.例如以上圖5的正視圖為圖6.
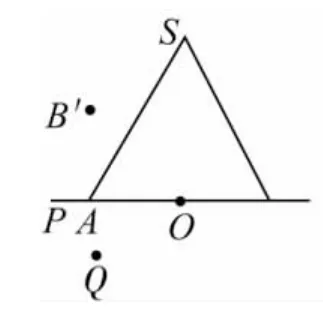
圖4
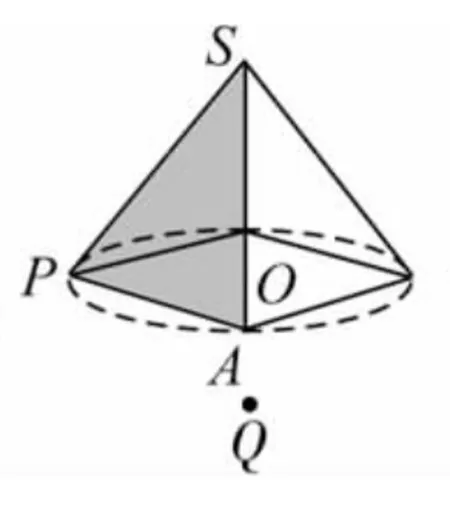
圖5
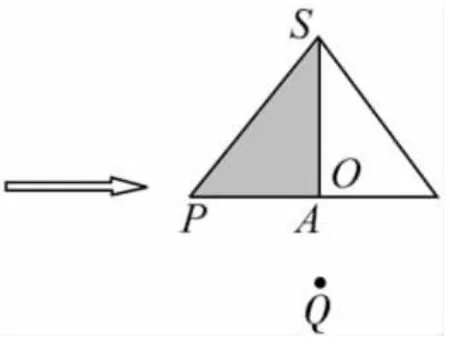
圖6
(值得一提的是,在點A旋轉過程中,底面其他三點要跟著點A一起運動,就必須與點A相關,這正是通過【迭代】得到正四棱錐的原因.)
3 左視圖
分析 左視圖是在側面內由左向右觀察物體得到的視圖.相當于人以點O為圓心順時針轉90°觀察圖形,但實際作圖時不可能人轉,可以換個主體,也就是人不動,將圖形以點O為圓心,逆時針轉90°,此時的“主視圖”便是真正的左視圖.
作法同主視圖,這里不再詳說了.
4 俯視圖(移動)
分析 俯視圖是在水平面得到由上向下觀察物體的視圖.它的特點之一是定點S和橢圓中心O重合了,即四棱錐的高退化為0;特點之二是從上往下看底面是內接于圓的正方形.因此動畫分為兩個過程,一個是定點S退化到圓心O,另一個過程是正方形的一頂點A運動到圓上點Q(伸縮比為1).
作法
(3)合并按鈕.以上兩個動作可以同時進行,選中按鈕【移動A→Q】和按鈕【移動 S→O】,點擊【編輯】/【操作類按鈕】/【系列】,在彈出的對話框中改變標簽為“俯視”,選擇“同時執行”,“末動作停止”,隱藏按鈕【移動A→Q】和【移動S→O】.單擊按鈕【俯視】,即可得到正四棱錐的俯視圖(如圖7)

圖7
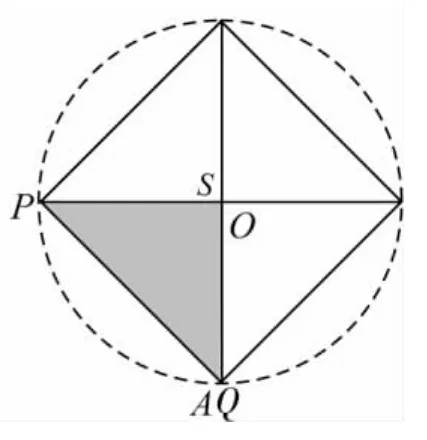
圖8
再點擊畫布上的【平動旋轉】按鈕,則正四棱錐水平放置的各種形式的俯視圖都可以呈現出來.例如以上圖5的俯視圖為圖8.
其他圖形如正五棱錐、正六棱錐等通過改變參數n的取值即可得到,而圓柱,直棱柱、球、立方體的三視圖都可以類似地作出來.
附錄:畫正四棱錐
作法 建立一個新的幾何畫板文件,進行如下操作
(1)作一個圓O,在圓上任取一點 P,選中點P,點O,點擊【構造】/【直線】,即得到直線 PO.
(2)制作橢圓.在圓上任取一點Q,選中點Q和直線PO,點擊【構造】/【垂線】,點擊兩直線交點 A'(立即在【顯示】菜單中【隱藏垂線】),即過Q作直線PO的垂線交點 A'.連接 QA',在 QA'上任取一點 A,選中點 A,Q,依次點擊【構造】/【軌跡】,即得到橢圓.
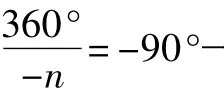
20111118)

