從一道習題的變式中培養學生的思維能力

443002 湖北省宜昌市二十五中學 鄭世圣

從一道習題的變式中培養學生的思維能力

443002 湖北省宜昌市二十五中學 鄭世圣

筆者在多年的課堂教學實驗中清楚認識到：充分地利用每一道習題，進行多解、多變、多用的訓練，培養學生的思維能力.

1 從一題多解中培養學生思維的發散性

原題 如圖1，AC∥BD，且分別與⊙O切于點A，B，在半圓上取一點E，過E點作切線CD交AC與BD于點C，D.AB為⊙O的直徑，半徑為r，求證：AC與BD的積為一常量(r2).

證法1 先證∠COD=Rt∠，由相似三角形得

證法2 證Rt△AOC∽Rt△BOD

證法3 ∠A+∠B=90°，解直角三角形

證法4 過點C引CF上BD，利用勾股定理

證法5 過O作OQ∥AC，則Q為CD的中點

點評 讓學生從這五種途徑中選出最優化的證法，再總結歸納證明中所運用的四基(基礎知識、基本技能、基本思想方法、基本經驗)進行一題多解的訓練，使學生從多角度、多途徑去思考問題，前后的知識技能得以綜合運用，增強了思維的發散性.

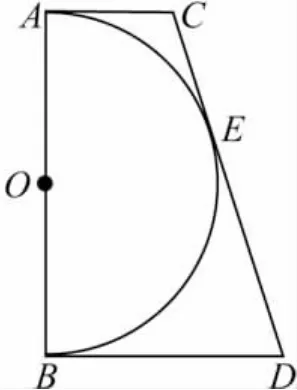
圖1

2 從一題多解中培養學生思維的獨特性

變式1 不改變原題中的條件，只將某些點連接起來，設OC交AE，⊙O于M，N，OD 交⊙O，BE于 G，H，從圖2中還可挖掘出更多的結論;

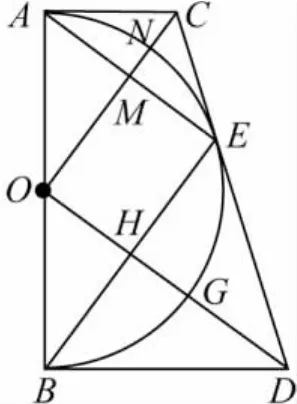
圖2

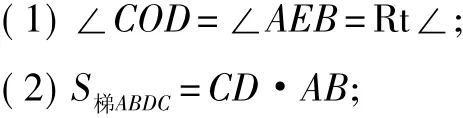
(3)四邊形BOED，AOEC為圓內接四邊形，且 OD，OC為直徑，并且都有內切圓;

(4)OC，OD分別為AE，BE的中垂線;

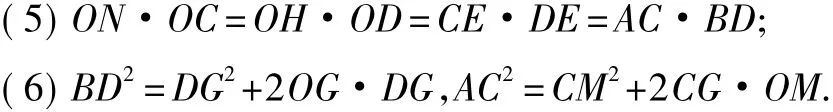
點評 教師根據此題特點，通過有意識提問為學生創設問題情境，引導學生從多角度、多方面由遠及近，由表及里，由特殊到一般，逐步向外延伸，使學生全面分析問題，悟出條件與結論之間的內在聯系，增強思維的獨創性.

3 從一題多變中培養學生思維的靈活性

變式2 改變條件，如圖3，以直角梯形的斜腰AB為直徑的⊙O切直角腰CD于E，若EF⊥AB于點F，求證：

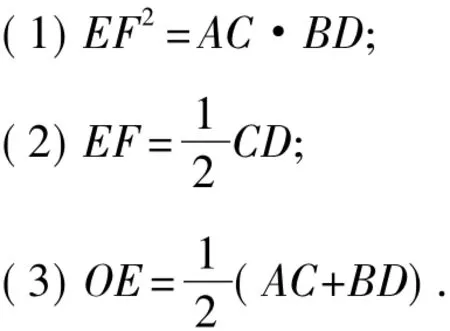
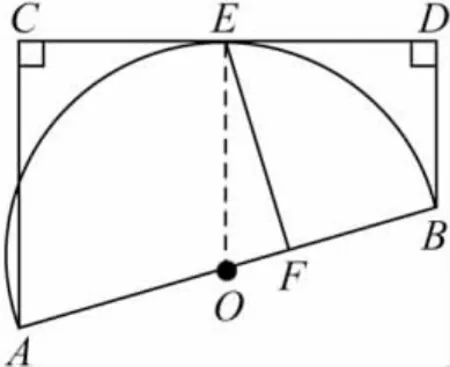
圖3

點評 “學習是原有認識結構對新知識的同化，是認識結構的組合和優化”通過一題多變，使學生更深刻認清基本質，掌握規律，達到舉一反三，聞一悟十的目的，一道習題繁衍出眾多的新命題、新結論，是對學生觀察、歸納、引伸多種能力的增強，培養了思維的靈活性.

20111012)