AGNES算法在K-means算法中的應用*

周愛武，潘 勇，崔丹丹，肖 云

(安徽大學 計算機科學與技術學院，安徽 合肥 230039)

K-means算法是基于劃分的經典聚類算法，該算法簡單、快速，得到了廣泛應用，但是該算法對孤立點是敏感的，其次該算法要求用戶必須事先給出簇數k值，該算法聚類結果受初始聚類中心隨機性選擇影響比較大，聚類中心選擇不當，容易導致聚類準確度下降，甚至無法得到聚類結果。針對以上缺點，國內外許多專家和學者提出很多對K-means算法的改進，比如參考文獻[1]~參考文獻[3]是基于密度的對K-means算法進行改進來找到密度比較高的代表點作為初始聚類中心，參考文獻[4]是把遺傳算法應用到K-means算法中來確定k個初始聚類中心，這種結合能夠進行一種全局優化，可提高算法的準確率，將智能算法與K-means算法的結合也是近年來研究的熱點。K-means算法以及其改進的算法已經應用到了各個領域，取得了很好的效果，比如參考文獻[3]是改進的K-means算法在客戶劃分中的應用，參考文獻[5]是在圖像標注和檢索的應用，參考文獻[6]是在存在異常孤立點大數據集中進行聚類發現簇的應用。由此可見，K-means算法的效率高、時間復雜度低，應用前景寬廣。

本文針對初始聚類中心隨機選擇這個缺陷，提出將凝聚層次聚類算法AGNES應用到改進的算法中，得到k個密度比較高的初始聚類中心，并將其應用到K-means中去進行聚類。實驗表明，改進的算法運行效率高，并能獲得比較高的準確率。

1 算法的基本思想

1.1 K-means算法

算法接收輸入量k，然后將n個數據對象劃分為k個聚類以便使得所獲得的聚類滿足：同一聚類中的對象相似度較高；而不同聚類中的對象相似度較小。聚類相似度是利用各聚類中對象的均值所獲得一個“聚類中心對象”來進行計算的。

K-means算法步驟描述如下：

輸入：n個數據對象，簇數k

輸出：k個簇的集合。

(1)從n個數據對象中任意選擇k個數據對象作為初始聚類中心。

(2)根據簇中數據對象的平均值，將每個數據對象依次劃分到最近距離聚類中心標志的簇中。

(5)如果E值變化明顯，將返回步驟(2)。

1.2 AGNES算法

[7]中提到的AGNES算法是凝聚的層次聚類方法。AGNES算法最初將每個對象作為一個簇，然后這些簇根據某些準則被一步步地合并。

AGNES算法描述如下：

輸入：包含n個數據對象的數據庫，終止條件簇的數目 c；

輸出：c個簇，達到終止條件規定簇數目。

(1)將每個數據對象當成一個初始簇；

(2)REPEAT；

(3)根據兩個簇中最近的數據點找到最近的兩個簇；

(4)合并兩個簇，生成新的簇的集合；

(5)UNTIL達到定義的簇的數目；

2 改進K-means算法

K-means算法初始聚類中心是隨機選取的，選取不當的話，將會無法得到正確的聚類結果。而AGNES算法將最近的數據對象聚集在一起形成簇，根據AGNES算法的這種思想，提出一種新的算法來確定k個初始聚類中心。

2.1 相關概念

定義1歐式距離

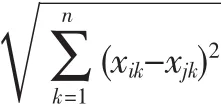
定義2點的密度

數據xi和距離α，以xi為圓心，α為半徑的區域內對象的個數 (包括圓心自身)記為該對象的密度，記為Density(xi)=(p 的 個 數|Distance(xi，p)≤α)， 其 中 Dis tan ce(.)為歐式距離，α取所有數據對象間距離和的平均值。

定義3平均密度

2.2 初始聚類中心的確定算法

Initial Clustering Center算法如下：

輸入：n個數據對象的數據集 DataSet，聚類簇數k，參 數 θ，ClusterSet、HighSet、CenterSet 3 個 集 合 開 始 均 為空。

輸出：k個初始聚類中心數據集CenterSet。

(1)將每個對象當成一個初始簇；

(2)REPEAT；

(3)根據兩個簇中最近的的數據點找到最近的兩個簇；

(4)合并兩個簇，生成新的簇的集合；

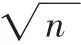
(6)計算數據對象的平均密度Ave；

(7)對步驟(5)中生成的c個簇將其加入到ClusterSet集合中，分別計算每個簇中數據對象的個數，將個數大于Ave的簇加入到HighSet集合中；

(8)令 i=1；

(9)如果HighSet集合不為空，執行步驟 (10)~步驟(13)；否則執行步驟(15)~步驟(18)；

(10)REPEAT；

(11)取出HighSet集合中數據對象個數最多的簇cx；

(12)計算該簇cx中數據對象的平均值做為第i個初始聚類中心，將其加入到CenterSet集合中去，并將簇cx從 HighSet和 ClusterSet中刪除，i=i+1；

(13)UNTIL得到k個初始聚類中心；

(14)如果步驟(10)~步驟(13)生成的初始聚類中心個數小于k，并且HighSet集合為空，即執行步驟(15)~步驟(18)；

(15)REPEAT；

(16)取出ClusterSet集合中數據個數最多的簇cx；

(17)計算簇cx中數據對象的平均值做為第i個初始聚類中心，將其加入到 CenterSet集合中去，并將簇cx從ClusterSet中刪除，i=i+1；

(18)UNTIL得到k個初始聚類中心；

(19)算法結束。

2.3 改進的K-means算法

改進K-means算法如下：

(1)運行 Initial Clustering Center算法，得到 k個初始聚類中心集合CenterSet；

(2)輸入 k值、k個初始聚類中心集合 CenterSet和數據對象集合DataSet；

(3)運行K-means算法，輸出K個聚類，算法結束。

3 改進后的實驗及分析

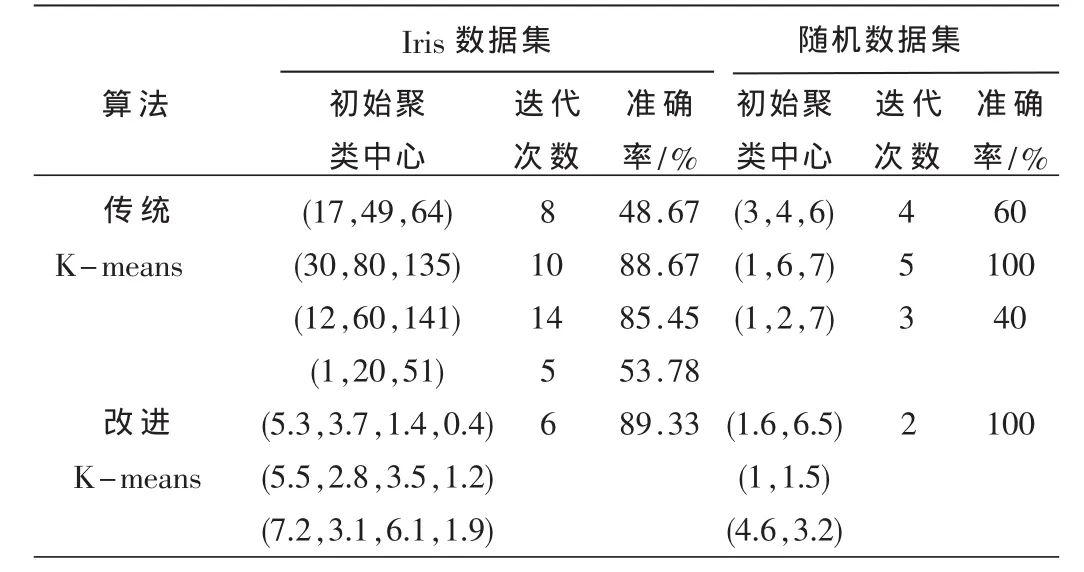
表1 傳統K-means算法和改進K-means算法的比較

從表1 Iris數據集可以看出傳統K-means算法的迭代次數有時比改進K-means算法要小，但是其準確率卻顯得很低。這說明K-means算法受初始聚類中心的影響比較大，一旦選擇不當，準確率將會很低，而優化的初始聚類中心是比較穩定的，符合數據對象的實際分布，同時可以盡快收斂最優解并且準確率高。從隨機數據集整體上來看，改進的K-means算法的迭代次數減少，收斂速度比較快，準確率很高。所以改進的K-means算法收斂速度比較快，得到的初始聚類中心符合數據對象的實際分布，提高了聚類準確率，達到了更好的聚類效果，同時該算法在煙草配送點分配問題等領域都得到了很好的應用。

本文結合層次聚類算法AGNES算法，提出一種確定初始聚類中心的算法，使得到的初始聚類中心比較穩定，符合數據的實際分布，避免選到孤立點，大大提高了算法的準確率和效率。同時改進的算法一個優點是能進行異常點的發現，能夠對網絡異常進行檢測。但是改進K-means算法的時間復雜度不如傳統K-means算法，所以今后的研究方向主要是針對大數據集在時間復雜度的提高上作進一步的研究，并將改進的算法應用到其他實際領域中。

參考文獻

[1]賴玉霞，劉建平.K-means算法的初始聚類中心的優化[J].計算機工程與應用，2008，44(10)：147-149.

[2]劉艷麗，劉希云.一種基于密度的 K-均值算法[J].計算機工程與應用，2007，43(32)：153-154.

[3]向堅持，劉相濱，資武成.基于密度的 K-Means算法及在客戶細分中的應用研究 [J].計算機工程與應用，2008，44(35)：246-248.

[4]孫秀娟，劉希玉.基于初始中心優化的遺傳K-means聚類新算法[J].計算機工程與應用，2008，44(23)：166-168.

[5]潘崇，朱紅斌.改進K-means算法在圖像標注和檢索中的應用[J].計算機工程與應用，2010，46(4)：183-185.

[6]ESTER M，RIEGEL H P.A density based algorithm for discovering clusters in large spatial databases with noise[C].Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining(KDD-96)， Ortland，Oregon，1996.

[7]毛國君，段立娟，王實，等.數據挖掘原理與算法[M].北京：清華大學出版社，2000年.