短波跳時跳頻信號的同步技術研究

梁東坡,周安棟,王永斌,屈曉旭

(海軍工程大學電子工程學院,湖北武漢430033)

0 引言

短波跳時跳頻技術具有很好的抗定位能力,而跳時跳頻同步是跳時跳頻通信的關鍵技術,只有實現了快速精確的同步,才能正確地接收和解調信息,因此同步系統是跳時跳頻通信系統的核心之一。跳時跳頻同步的關鍵是跳時同步和跳頻圖案的同步,目前的同步多采用包含時間信息的同步字頭,將攜帶有時間信息的同步頭置于跳頻信號的最前面,收端從同步頭中捕獲到同步信息后調整本地跳頻序列發生器,從而使收發雙方實現同步。這種同步方法具有同步搜索快、易于實現以及同步可靠等特點[1,2,7],但是在跳時跳頻系統中,信號發送比較慢,采用這種同步方法,占用時間資源較多,所以該文基于跳時跳頻信號特征和考慮節約時間資源,提出一種跳時跳頻信號同步方法。

1 跳時跳頻信號同步原理及捕獲

1.1 同步方法原理

傳統的同步方法采用的同步頭+TOD信息在這里不適用,因為這樣導致幀同步頭過長,現在采用一種去掉TOD信息的同步頭,同步頭與跳時PN碼和跳頻PN碼為一一對應關系,信號接收下來同時送入FPGA模塊和DSP模塊,在同步過程中用滑動窗與接收的信號做相關,檢測幀同步頭的到來,在FPGA中做幀同步,然后在DSP中做位同步,提取幀同步頭信息,得到跳時、跳頻PN碼信息,控制跳時、跳頻PN碼產生模塊輸出與發送端相同的跳時、跳頻PN碼以進行信號的準確接收。

1.2 幀同步過程

接收信號經過A/D轉換和下變頻后分別送到FPGA和DSP中,在FPGA中進行信號幀同步檢測,采用滑動窗相關檢測的方法。一個碼元持續時間為T。取與同步頭長度相等的接收信號與同步頭進行相關,為保證不漏掉同步頭中的某個碼元,每次滑動半個碼元(T/2,也是一個時間元持續時間)再做相關,相關值最大的信號為當前同步頭信息,取其接收時間為當前信息接收時間,并存儲檢測值次大的相關值、接收信息時間、最大和次大之間的移動方向,檢測過程如圖1所示(接收窗超前信號窗口)。

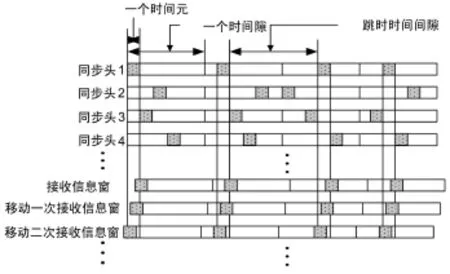
圖1 滑動窗相關檢測

在做滑動窗相關檢測時是接收信息同時和同步頭庫中的所有同步頭做滑動相關,找出最大為當前使用的同步頭。因為每次滑動 T/2的長度,在幀同步結束時,可以捕獲到同步頭75%的能量,也就是說采樣時刻與接收碼元之間的時間偏移最大值Δ tmax=T/4。

1.3 位同步過程

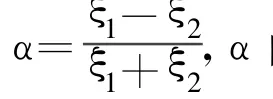
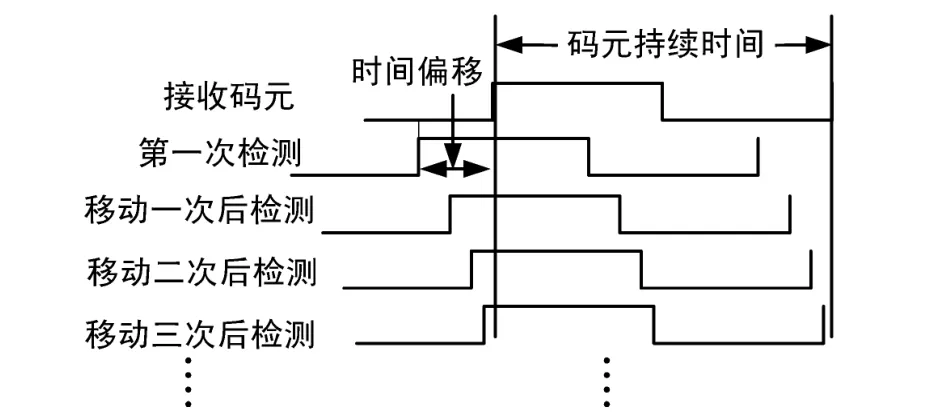
圖2 接收時刻超前碼元時刻

當接收時刻滯后碼元時刻時位同步時,位同步示意圖與接收時刻超前碼元時刻的情況類似。

2 同步性能分析

2.1 同步時間

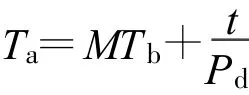
2.2 檢測概率和虛警概率

在加性高斯白噪聲(AWGN)信道分析同步系統的性能,給出同步系統的檢測概率Pda和虛警概率Pfa。

當無信號存在并且無干擾時,由文獻[4]則虛警概率為：

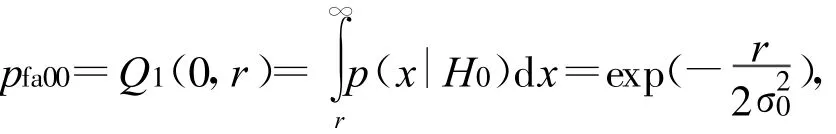
式中,r為判決門限,Q1(?)為馬庫姆函數。

當有信號存在且不存在部分頻帶干擾時,檢測概率為：

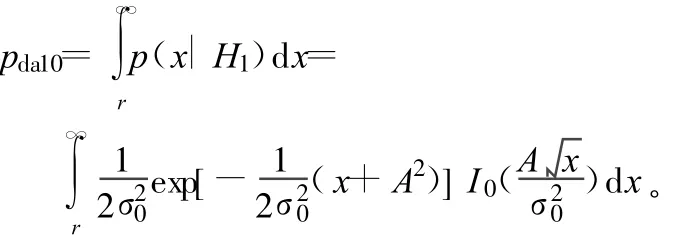
當無信號存在且有部分頻帶干擾時,虛警概率為：

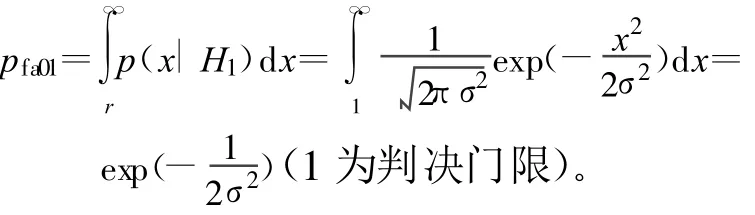
當有信號和部分頻帶干擾同時存在時,檢測概率為：

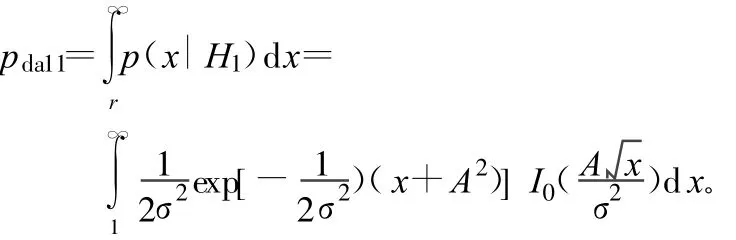
綜合上面4種情況,AWGN信道下,虛警概率和檢測概率可表示為：

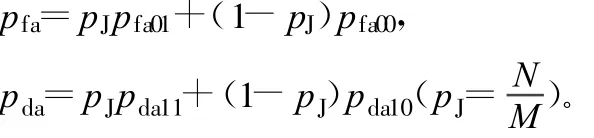
同步頭中包含M跳同步序列,因此同步頭的虛警概率和檢測概率為：

3 同步性能仿真

AWGN信道下,考慮干擾,虛警概率、捕獲概率與信噪比、判決門限以及干擾功率之間的關系,噪聲為歸一化噪聲。圖3為高斯白噪聲下虛警概率Pfa和判決門限r之間的關系(考慮干擾存在的情況)。

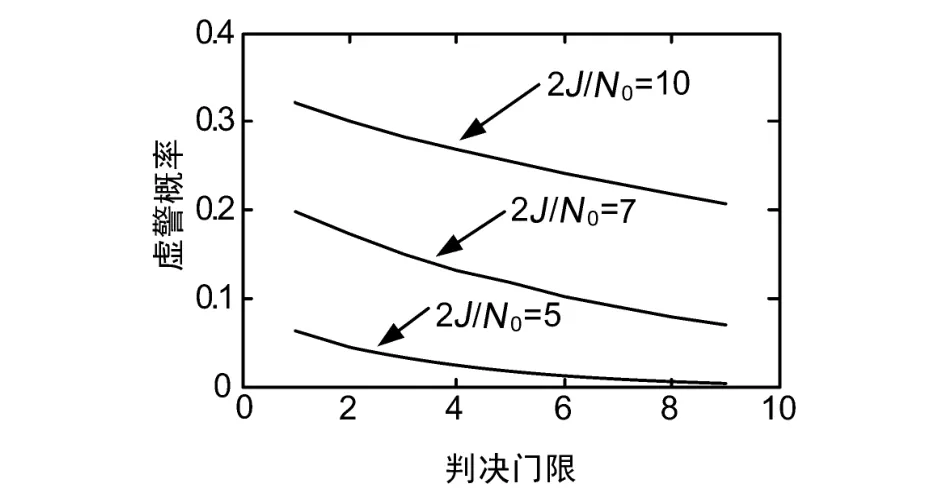
圖3 虛警概率與判決門限和干擾功率的關系

圖3表明,虛警概率Pfa隨著判決門限r的增大而減小,當 r=6.8時,Pfa=0.01,隨著干擾功率與噪聲功率比J/N0的增大而增大,所以存在干擾時,虛警概率大于無干擾時的虛警概率。

圖4為高斯白噪聲下捕獲概率和虛警概率、信噪比之間的關系(考慮干擾存在的情況),由圖可以看出,存在干擾時虛警概率為0.01,信噪比大于3.5 dB時,捕獲概率可以達到95%以上;相同信噪比下隨著虛警概率的減小,檢測概率減小,圖中虛警概率Pdf取到。

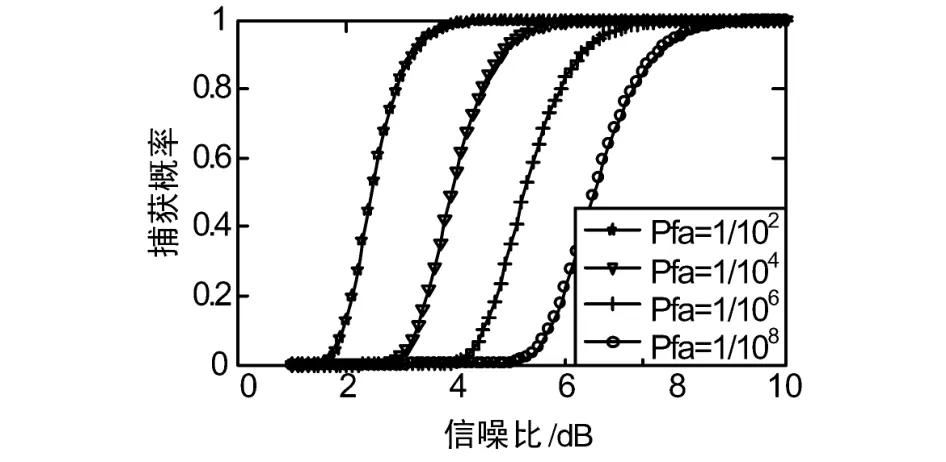
圖4 捕獲概率和虛警概率、信噪比之間的關系

圖5為高斯白噪聲下捕獲概率與干擾頻點數和信干比之間的關系,取虛警概率 Pfa=0.01,信噪比Es/N0=4,E/J為信干比,由圖可以看出,隨著干擾頻點數的增大,捕獲概率相應增大,捕獲概率均達到97%以上。

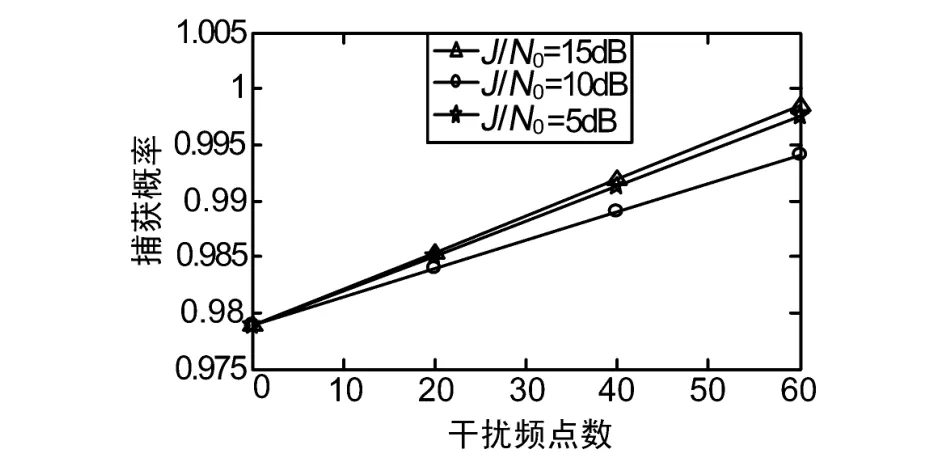
圖5 高斯白噪聲下捕獲概率與干擾頻點數的關系

4 結束語

采用了新的同步方法,分別探討了有無干擾2種情況下,在高斯白噪聲信道下虛警概率、捕獲概率及捕獲時間等,并對其進行了仿真。由參考文獻[8]跳頻同步可靠性指標,同步系統仿真說明：在干擾存在的情況下,該系統具有較高的捕獲概率,能夠進行穩定地同步,還具有同步時間較短的性能。

[1]DIXON R C.Spread Spectrum Systems[M].NewYork：John wiley,1976：76-83.

[2]SCHOLTZ R A.The Spread Spectrum Concept[J].IEEE Trans Commun,1977,25(8)：748-755.

[3]趙樹杰,趙建勛.信號檢測與估計[M].北京：清華大學出版社,2005.11：33-45.

[4](美)HOLMES J K.相干擴展頻譜系統[M].梁振興譯,國防工業出版社,1991：468-499.

[5](美)PROAKIS JG.數字通信(第 4版)[M].張力軍,張宗橙,鄭寶玉等譯,北京：電子工業出版社,2009：216-223.

[6]李少謙,董彬紅,陳智.差分調頻通信原理及應用[M].成都：電子科技大學出版社,2007：61-67.

[7]任玉升,唐向宏,廖見盛.跳頻通信系統的一種同步方法探討[J].電子對抗,2004(3)：23-26.

[8]鄢茂林,蔣子剛,涂衛紅.跳頻同步可靠性指標探討[J].電訊技術,2009(5)：63-66.