基于模糊神經網絡的火災信號處理設計
王慶暉
(四川瀘定縣公安消防大隊,四川甘孜626100)
火災監控系統中關于火災信號處理的結構可分為3層:處理信號層、判斷信號層與決策信息層。其中,信號處理層可以將火災識別的種類分為非火災源、陰燃以及明火,并由此在大多數場合下可推斷出發生火災的概率;而最后的信息決策層則是根據判斷層所輸出的信息,利用相應的判斷規則以及決策技術將火災的最終結果決策出來。
1 軟件Matlab 7介紹
20世紀80年代,美國的 Math Works公司推出了一款數學軟件即Matlab。這款軟件是十分高效的,可用于仿真建模、設計算法、設計概念,是讓人滿意的一種集成環境。數值運算的不斷進化,使得它漸漸演變成科學可視化的、各種數字信號處理、系統仿真的通用標準語言。作為三大數學軟件之一,其強項就是仿真以及強大的矩陣計算能力。而Matlab的編譯器是自給自足的:兼容了Fortran以及C++兩大語言;因此,可以說 Matlab是研究者或者工程師用作研究的最佳的語言,而且是最佳的環境以及工具[1]。Matlab通過自我改善,至今為止,已經演變成具有非常強大作用的軟件之一。
Matlab 7將文件I/O、數字計算、數據可視化、代碼效率、編程環境等方面進行了升級:
(1)開發環境
桌面環境經過重新設計,就多文檔界面應用問題提供了訪問方法和簡單的管理,增強了工作空間瀏覽器和數組編輯器功能,提高了M文件編輯器的功能,并支持各種格式源代碼文件的可視化編輯,如Java,HTML,C/C++等。
(2)編程效率提高
支持創建匿名函數和嵌套函數功能,并增強了注釋模塊化的功能。
(3)便捷高效的數學運算
支持單精度的數據類型運算,如FFT、線性代數、基本算術運算等,支持整數的算術運算。
(4)可視化的3D和圖形
圖形在窗體界面上表現出新型化,從圖形的窗體上直接產生M代碼,方便用戶做完繪圖,并為觀測手段提供了豐富的數據。
(5)外部接口和文件I/O
新增加了文件I/O,讓MAT文件具備了數據文件快速I/O 的能力,并支持 Unicode,FTP,SOAP,VBS,COM 編碼。
動態交互式系統研究、模擬及建模的圖形環境,是嵌入式系統研究的基本環境。
2 信號處理層
火災的發生后,火情發展千變萬化,在這個過程中還伴隨CO氣體濃度變化、煙霧產生以及溫度升高等特征變化。本文由CO濃度、感煙和感溫3種傳感器測查各現場。鑒于信號的范圍是根據干擾源的變化而變化的;因此,要對收集到的信號進行預處理,包含放大、整形濾波等[2]。在輸入神經網絡和模糊控制器之前,還要對信號數據進行歸一化處理。
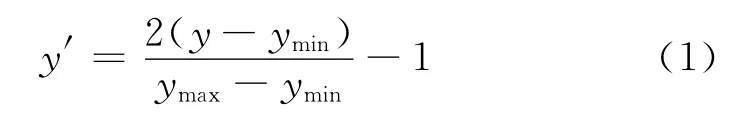
式中,y′為預處理數據;y 為樣本數據;ymin,ymax分別為樣本數據的最小值和最大值。
3 處理模糊控制的火災信號
模糊控制器設計包括方面:① 確定模糊控制器的輸出變量和輸入變量;② 設計控制器結構;③ 明確隸屬度函數;④ 設計流程方式;⑤ 將控制方式進行清晰化或模糊化。具體流程如圖1所示。
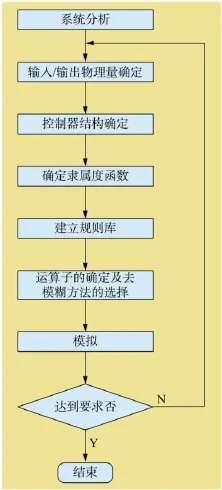
圖1 設計模糊控制器的流程
3.1 輸入量的模糊化
在啟動模糊化運算時,需要尺度來變換輸入量,將尺度變換到一個適合的區間。如一個爐子的溫度是850℃時,可將其變成為語言的數值,用高、中、低3種方式表示。通常情況下,操作以一個物理量分為負大(NL)、負中(NM)、負小(NS)、零(ZE)、正小(PS)、正中(PM)、正大(PL)7級變量。語言值需要與每一個模糊子集一一對應,常采用梯形、三角形或其他形狀的基礎圖形作為其函數[3]。三角形屬于非常容易計算的函數,其圖形非常簡單,故得到了廣泛使用,其隸屬函數圖如圖2所示。
隸屬函數解析式為
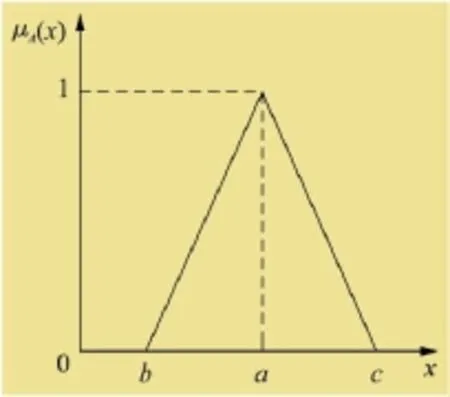
圖2 三角形隸屬函數圖
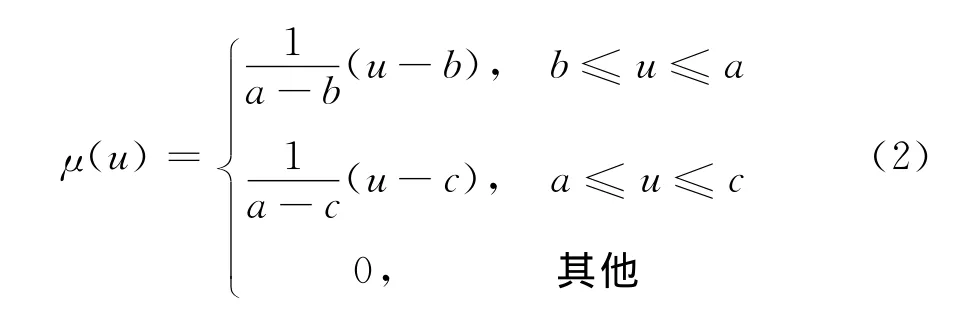
式中,μ為模糊控制器輸出的隸屬度函數;a為模糊集的中心;b,c分別為模糊集的2個端點。
系統采用是三角形隸屬函數。根據火災發生時情況,將CO、煙霧的濃度以及環境中的溫度這三者的信號表示為無火情,火情可能性小和火情可能性大。
3.2 創建推理法則
在推理過程中,設計規則庫時,應確定控制規則的數目和語言的變量級數,并正確地建立規則形式[4]。
模糊控制規則是對系統控制經驗進行的概括總結,是控制器設計最為重要的依據之一,它對控制系統有著非常大的影響。所以,制定一套科學、合理的規則就顯得尤為重要。在創建相關規則時,必須將控制規則的特點考慮在內。
從以上模糊控制的規則要求可以系統地得出模糊規則。
3.3 反模糊化
有各種方法可以進行去模糊處理,其中最常用、簡單的有加權平均法、中位數法和最大隸屬度法[5]。其判斷方法為

式中,u′為模糊規則輸出;μc(ui)是對應用的第i個規則的輸出隸屬函數;ui為模糊集中的離散點;m為規則數。
3.4 基于模糊控制的火災信號處理結果分析
從信息角度分析,模糊的辨識是非常規則型的一類權威型的系統。模糊邏輯可以在火災探測中被采納,需要建立非常規范的傳輸關系庫。本文傳輸對應的信號都是指在傳感器模糊化后的,而傳輸中輸出所對應的是發生火災的概率為多大。整個算法的重點是建立1個非常規范的規則庫。影響火災的因素很多,受不同燃燒的環境、燃燒物質等因素的影響,人們無法從現有的資料中去總結出相關的規律及其函數。然而模糊技術最為重要的一點就是確立模糊的規則[6]。只有當規則精準、覆蓋全面,才能識別出正確的結論。所以,僅依靠模糊邏輯,理想的辨識結果是無法達到的。
4 神經網絡火災信號的處理
神經網絡搭建的方式比較多樣,根據目前最流行的方法大致可分為反饋、前向的網絡。多層前向網絡使用較頻繁,最常見的是徑向基函數(Radial Basic Function,RBF)神經網絡和誤差反向傳播前饋(Backpropagation,BP)神經網絡模型,此外,還有一種是在這兩者基礎上經過多次改進的模型[7]。
常見的BP網絡包含了神經網絡理論中最精華的部分,因為其可塑性強、結構簡單,故在數據壓縮、信息分類、模式識別及函數逼近等領域被廣泛應用。
BP算法步驟如圖4所示。
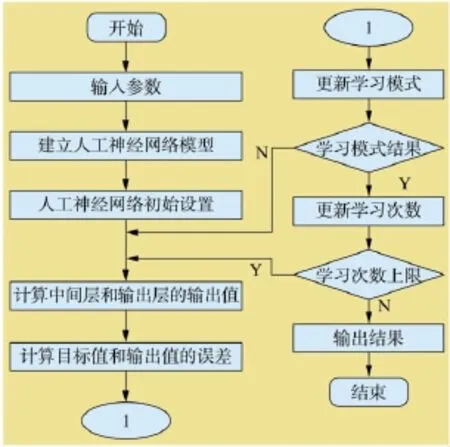
圖4 BP神經網絡算法流程圖
BP算法的缺陷包括:① 容易形成局部極小而無法達到全局最優;② 由于訓練次數多導致收斂速度減慢,學習效率下降;③ 選取隱節點缺少理論作為支撐;④ 在鍛煉時忘記老樣本、學習新方式的現象頻出。
優化BP算法的方法可分為網絡結構調整、權值調整等。但是使用最多的包括:①Lcvcnberg-Marquart算法;② 共軛梯度算法;③ 學習速率調整;④ 加入動量項。除了改進算法外,通過調整誤差、改變網絡結構等,也可以加快BP算法的收斂速度[8]。
設計BP網絡過程如下:① 輸出層和隱層間的權值為W2,而隱層和輸入層間的權值為 W1,第3層為輸出層,第2層為隱層,第1層為輸入層;② 歸一化后的CO的濃度、煙霧濃度和溫度為輸入向量,輸出向量為明火、無火、陰燃的概率,其取值范圍為0~1;③ 雙曲正切的S型的傳遞函數為隱藏激活函數,而輸出的相關函數為S型對數函數;④ 訓練函數分別選定Levenbeg Marquadt BP訓練函數、準牛頓函數以及梯度下降函數來鍛煉;⑤ 按照經驗可將隱層結點數設為7~13,并通過比對來選擇最為合適的;⑥ 網絡結構是3層前向的網絡,用BP算法計算。
對隱層神經元數目進行優化是極為困難的問題,設計者一般需要根據自身的經驗及多方面的實驗來選擇最終的數目;因此,用理想數學表達式表示是不可能的。但是,隱層神經元的數目、傳輸相關單元的數目、問題的要求都應該有著直接或間接的影響,最優的一個隱單元數一定隱藏在這其中。對隱單元數作最優選擇時可參考。
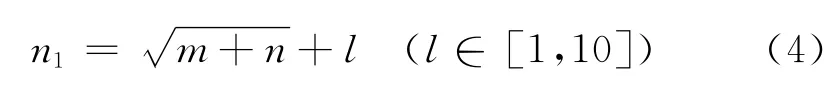
式中,m為輸出單元數,n為輸入單元數;n1為隱單元數。
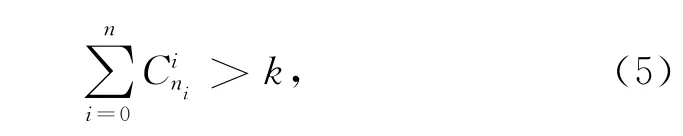
式中,k為樣本數;若i>n1,則Cini=0。

理論上,最佳的連續函數逼近是RBF網絡。RBF有較好的泛化能力,只需改變少量的權值以及節點[9],學習會比一般的BP算法提升數千倍的速度,更容易掌握和了解新的數據和資料,其收斂性也比BP網絡好,可以得到最優解。
5 控制與網絡的有機合并
模糊邏輯最習慣使用的運算法則被稱之為最大、最小規則,如果使用最大、最小法則就有可能丟失了部分信息,然而這種運算對于抓住相關的主要信息并且迅速做出回應或處理是十分有利的[10]。因為權重是可以用學習來更改相關數值的量,起到增加數據獲取以及存儲的作用。
將實現高級智能作為最終的發展方向,把模糊控制技術以及人工神經網絡相輔相成地融合在一起,以彌補其中不足,是研究者們值得研究并且完善的主要目標。
依據神經網絡連接、模糊系統的運用的方式及相關的使用功能,將兩者合并的方法大致可分為并聯型結合、松散型結合等5種[11]。
5.1 采用模糊神經網絡的系統
3種不同的探測器從不同的角度探測火災的相關信息,并將測量到的相關信號作為火災信號的警戒信息,為探測火災提供了充實的依據;為進一步提升響應時間的靈敏度和可靠性,分別將輸入信號送入神經網絡和模糊系統,再經過模糊邏輯判斷后輸出。實現框圖如圖5所示。
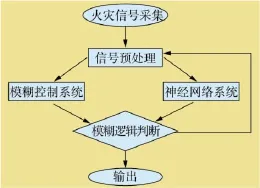
圖5 模糊神經網絡火災信號的處理框圖圖示
5.2 信息決策層
根據神經網絡系統、模糊控制系統得出的結論,通過系統的分析并且使用一定的模糊邏輯進行判定,得到最后目標是信息決策層主要的任務。神經網絡系統輸出明火的概率設為m1,陰燃火的概率設為m2,無火的概率設為m3,以及模糊控制器所得到的火災概率這幾者存在一定的沖突。不難得到以下結論:當神經網絡判斷為無火m3并且模糊邏輯傳輸出的信息,火災概率k>0.6時,可以確定有火災出現;可是,當神經網絡認為火災是非火災源而且模糊邏輯所傳輸的火災概率k>0.3時,就難以判斷是否出現了火災[12]。由于得到的實際火災數據較少,無法代表所有的火情,再加上神經網絡的泛化能力有限,對于模糊邏輯控制器的規律的了解也不夠深入。同時,模糊神經網絡輸出當做判定火災的依據的標準還有明顯的局限性,故往往是將神經網絡系統輸出明火的概率m1與模糊邏輯所傳輸的火災概率k再次融合,并結合人們的經驗判斷,最終得到火災概率。
如果把神經網絡輸出的無火概率m1,陰燃火概率m2,明火概率m3以及模糊控制器所推斷的火災概率0當做模糊邏輯判決進行分析并且輸入。其判定的標準可規定如下:
當m3≥0.6,且0.3≤k≤0.6,判斷為延時t s再進行判斷;
當m3≥0.6,且k≥0.6,則可以判斷為明火火災;
當0.3≤m1≤0.6,且k≥0.6,判斷為延時t s再進行判斷;
當m2≥0.6,且k≥0.3,判斷為陰燃火火災;
當0.3≤m2≤0.6,且k≥0.3,判斷為延時t s再進行判斷;
當m2≥0.6,且k≤0.3,判斷為延時t s再進行判斷;
當m1≥0.6,且k≤0.3,則判斷為無火災發生;
當m1≥0.6,且k≥0.3,判斷為延時t s再判斷。
6 結 語
本文闡述了火災監控的相關系統及火災相關信號處理系統的3個層面上的結構,其中對于信號的判斷層進行詳細地分析介紹,利用模糊系統及人工神經網絡依次對處理層進行相關的預處理,然后傳輸相關的信號作為火災判斷的依據。提出了決策層中對神經網絡輸出用模糊邏輯的推理系統及采用模糊邏輯系統的輸出方式,對模糊邏輯進行再次推理分析,最終無論推斷出何種結論,利用延長t s,再次采集相關的火災信號的方式來獲得最有說服力的結論。
[1] 李 峰,田繼東,楊冬永.火災早期探測技術的發展及其展望[J].機械管理開發,2008,18(12):62-63.
[2] 許 東,吳 錚.基于 MATLAB6.X的系統分析與設計——神經網絡[M].2版.西安:西安電子科技大學出版社,2002.
[3] 徐金明.MATLAB實用教程[M].北京:清華大學出版社,2005.
[4] 王 娜,徐風榮,劉海龍.火災探測的模糊神經網絡數據融合技術[J].控制工程,2007,23(5):44-49.
[5] 劉 維.精通 MATLAB與 C/C++混合程序設計[M].北京:北京航空航天大學出版社,2005.
[6] 趙玉寶.火災報警技術分析[J].消防技術與產品信息,2009,17(2):38-40.
[7] 王沐然.MATLAB與科學計算[M].北京:清華大學出版社,2008.
[8] 馬偉明,秦科雁.極早期火災智能預警系統的分析研究[J].消防科學與技術,2009,34(3):33-36.
[9] 張國良.模糊控制及其 MATLAB應用[M].西安:西安交通大學出版社,2007.
[10] 谷建榮,社成寶.模糊控制技術在模擬量火災報警系統中的應用[J].原子能科學技術,2000,34(5):439-444.
[11] 羅云林,朱瑞平.基于數字圖像處理的火警監測系統研究[J].遼寧工程技術大學學報:自然科學版,2002,21(6):754-756.
[12] 陳 濤,袁水宏,范維澄.火災探測技術研究的展望[J].火災科學,2001,2(10):108-110.

