四原子Tavis-Cummings 模型中兩體及多體糾纏的研究

吳坤華，張建松，張小青，王 洵

（1.華東交通大學應用物理系，江西南昌330013；2.北京建筑工程學院，北京100044）

眾所周知量子糾纏是量子信息發展過程中重要的量子資源之一，它是眾多量子協議得以實現的重要依托[1-2]，而QED腔提供一個很好的操控量子糾纏和展示量子信息過程的平臺[1-4]。其中，J-C模型[5]就是人們最熟悉和引用最廣的場與原子相互作用的模型之一，J-C模型展示的是量子化的場與量子化的二能級原子之間相互作用之間的全量子化過程。擁有很多純量子化特性，如：Rabi震蕩下的塌縮與復活；場的壓縮；光子反群聚等在J-C模型都有很好的展示[6-7]。

該文探討的主要內容是Tavis-Cummings（簡稱T-C）模型[8]下4個二能級原子之間糾纏的演化情況。T-C模型主要描述的多個二能級原子與單模場之間相互作用[6-7]。它可運用于量子信息過程和加深對基礎量子力學的理解[2，8]。在文獻[9]中，作者就運用tangle運算方法對兩原子的T-C模型的量子糾纏進行了探討和研究。這里將對四個二能級原子在一個光學腔中的相互作用情況進行討論，主要是對不同原子之間相互作用和原子與場之間相互作用的探討。假設所有原子開始都處于基態，腔場處于粒子數態。首先，將討論如何獲得量子化系統；其次，將運用concurrence和tangle對系統在兩兩相互作用情況下的糾纏進行計算；最后，將討論在一定條件下，原子與腔場相互作用時系統量子態的表示（W態）。

1 模型的選擇和討論

在旋波近似情況下，4個二能級原子在T-C模型下的哈密頓量可表示為[8-10]：（文章中取 h=1）

式中：gi為場和原子之間相互作用的系數；為原子的上升算符；σi-為原子的下降算符；wi為二能級原子的躍遷頻率；a+，a為原子的產生和湮滅算符；w為腔場的頻率。系統模型為4個二能級原子與1個單模腔場的相互作用系統，其中原子間距離足夠大，因此原子間相互作用可忽略。如圖1。

圖1 四個二能級原子與一個單模場相互作用系統Fig.1 Interaction system of four two-level atoms and a single-mode field

下面，將對系統做一定的假設，以便有利于系統的計算，假設原子的躍遷頻率與腔場的固有頻率相等；原子與原子之間的相互作用系數和原子與腔場之間的作用系數相等，即w=wi，g=gi。因此，系統的哈密頓量可表示為

2 concurrence和tangle的運算及比較

由運動方程和系統的初始態情況可知[11]，系統任意時刻t的量子態表示為

由于能量守恒定律（即旋波近似情況下），在這里省略了快變量項eiw/2。（在運算式中，用大寫字母C表示concurrence的值）

下面，將對該系統運用concurrence進行糾纏度量的運算，由concurrence得定義為[12]

式中：λi(i=1，2，3，4)為約化密度算符本征值平方根，且當 λ1≥λ2≥λ3≥λ4時，反轉自旋約化密度算符 R 為

σy表示Pauli矩陣算符，有，而且，約化密度矩陣可表示為

（*表示復合函數的復共軛）在這種情況下concurrence可以表示為

首先，對腔場與第i原子之間的糾纏情況予以分析，在約化掉其他原子的情況下，可以得到腔場與第i原子之間的約化密度矩可以表示為

這里a1(t)=cos(2gt)；a2(t)=-isin(2gt)/2，聯立（8）（9），腔場與原子i之間相互作用concurrence表達式可寫為

原子i與原子 j之間相互作用的約化密度矩陣可表示為

同上，原子i與 j原子之間相互作用concurrence表達式可表示為下面，對Cfa1(t)和Caiaj(t)隨時間t的變化進行作圖，并進行對比分析，如圖2所示。

圖2 ConcurrenceCfa1(t)和Caiaj隨時間t在弱相互作用下(0＜g＜1)時演化情況Fig.2 Evolution of concurrenceCfa1(t)andCaiajwith time t in weak interaction region(0＜g＜1)

由圖2可以看出，隨著相互作用系數g的不斷加強，在一個周期內，腔場與原子之間的concurrence Cfa1(t)出現不穩定的變化，且變化周期越來越小；然而，原子與原子之間的concurrenceCaiaj(t)非常穩定，這也就是說在該系統中不管相互作用系數g如何變化，原子與原子之間的concurrenceCaiaj(t)不變。

現在，對該系統運用tangle運算方法來探討該系統中多體糾纏之間的關系，這種運算方法首先由Coffman，Kundu和Wootters提出[13]，主要觀點是：系統中某一粒子或腔場與系統中其他粒子或腔場組成的整體之間的糾纏關系，并且討論了系統的糾纏分配情況。在tangle中某一qubit與系統其他部分（rest）的關系可以表示為[10]

其中ρ1是系統中原子1的約化密度矩陣。由tangle定義可知只有整個系統處于純態時，才可運用其對系統進行運算。由（4）（13）可以得出在約化腔場后的表達式：

同理，可以得出在約化任一原子后得tangle表達式：

下面，將對τf，(a1a2a3a4)(t)和τa1，(fa2a3a4)(t)的tangle函數隨時間t變化進行畫圖，并對它們的圖線進行對比和分析。如圖3所示。

從圖3（a）tangle τf，(a1a2a3a4)(t)和圖3（b）τa1，(fa2a3a4)(t)隨時間 t及相互作用系數 g 的演化圖像中，可以知道隨 著 g 的 變 化 τf，(a1a2a3a4)(t)的 周 期 變 化 比 τa1，(fa2a3a4)(t)周 期 變 化 要 快 ，且 還 可 以 看 出τa1，(fa2a3a4)(t)≥ τf，(a1a2a3a4)(t)。由圖2和圖3，可以看出 τf，(a1a2a3a4)(t)，τa1，(fa2a3a4)(t)都大于 Cfa1(t)，Caiaj(t)。而且，可以得出 τf，(a1a2a3a4)(t)≥ Cfa1(t)≥C2fa1(t)和 τa1，(fa2a3a4)(t)≥ Caiaj(t)≥ C2aiaj(t)，結果與文獻[13]相符，由推導可以得出：

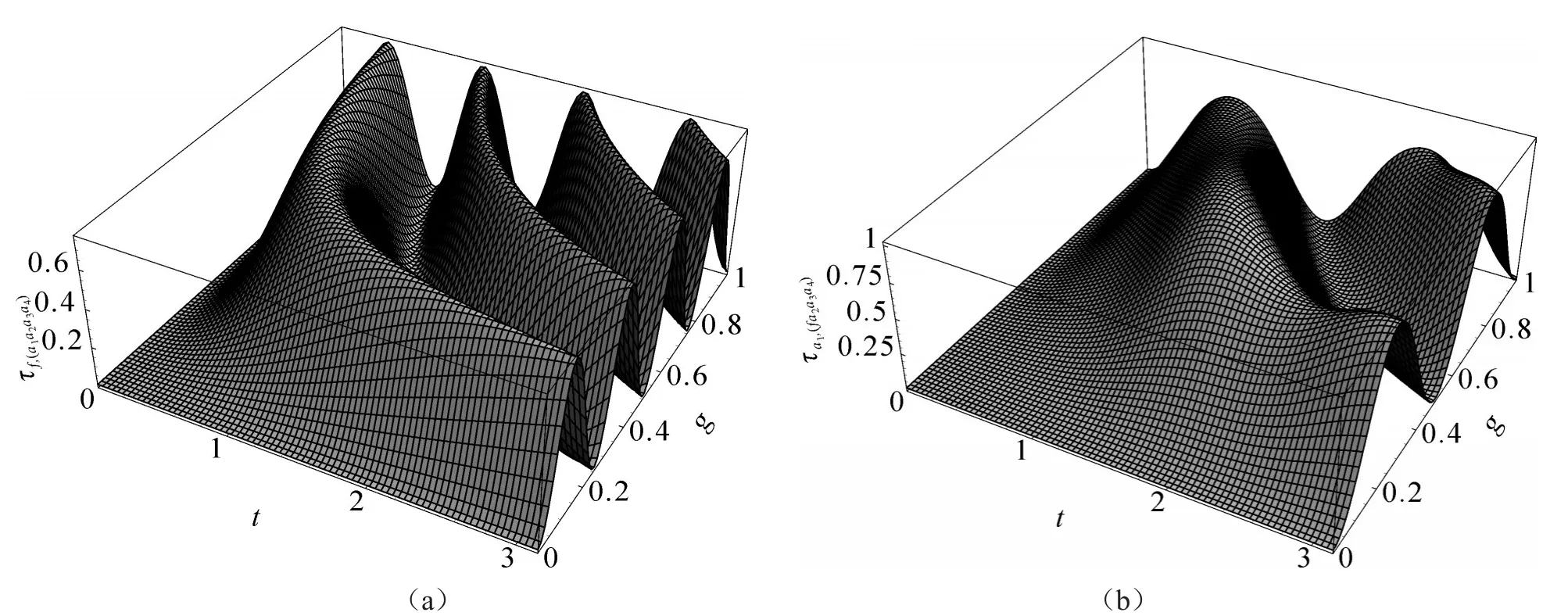
圖3 Tangle τf，(a1a2a3a4)(t)和tangle τa1，(fa2a3a4)隨時間 t及相互作用系數 g 的演化情況Fig.3 Chang of tangle τf，(a1a2a3a4)(t)and τa1，(fa2a3a4)(t)with time t and interacting constant g

這說明tangle運算過程中都是兩體之間的糾纏，而不存在三體糾纏[13]。由文獻[10][14]可以知道，腔場與原子及原子與原子之間的相互作用產生糾纏隨原子數的增加concurrence和tangle都在不斷變小，而原子之間相互糾纏的concurrence在各自系統中卻保持不變。

值得注意的是在表達式（4）中，當表達式的第一項系數為0時，即當時間t滿足以下條件時：

表達式（4）可表示為W態

這里運用了三角函數特性：當cos(2gt)=0時，sin(2gt)=1。從（17）式，由結果可以看出該式即為二能級原子系統的W態。也即在一定的條件下，W態可以由一個單模腔場與多個二能級原子相互作用系統來制備。

3 總結

主要討論在T-C模型下，1個單模腔場與4個二能級原子之間的相互作用情況下的糾纏演化。通過運用concurrence和tangle對系統糾纏量進行了詳細的計算和分析，兩種方法的共同點是：原子之間的相互作用產生的糾纏明顯大于或等于腔場與原子相互作用產生的糾纏，即Caiaj(t)≥Cfai(t)。然而這兩種方法也有各自的特色，如：由concurrence可知，原子與原子之間的相互糾纏量并不隨時間及它們之間的相互作用系數改變而改變，原子與原子之間相互糾纏相當穩定，因此對實際應用有很大的幫助。由tangle結果可知：場與原子之間的糾纏變化明顯比原子與原子及場之間的糾纏的變化不相同，且τa1，(fa2a3a4)(t)≥τf，(a1a2a3a4)(t)；而且，當在一定條件下，可以使得單模腔場與多個二能級原子相互作用情況下制備W態。

[1]TERHAL B M.Detecting quantum entanglement[J].Journal of Theoretical Computer Sicence，2002，287(1)：313-315.

[2] BENNETT C H，BRASSARD G.Quantum cryptography：public key distribution and coin tossing[C]//Proceedings of the IEEE International and Conference on Computers，Bangalore：Systems and Signal Processing，1984：175-179.

[3]SHOR PW.Scheme for reducing decoherence in quantum computer memory[J].Phys RevA，1995，52：2493-2496.

[4] BENNETT C H，BRASSARD G，CREPCAU C，et al.Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels[J].Phys Rev Lett，1993，70（2）：1895-1899.

[5] JAYNES E T，CUMMINGS F W.Comparison of quantum and semiclassical radiation theories with application to beam maser[J].Proc IEEE，1963，51（1）：89-109.

[6]MANDEL L，WOLF E.Optical choherence and quantum optics[M].Cambridge：Cambridge University Press，1995.

[7]SCULLY M，ZUBAIRY M S.Quantum optics[M].Cambridge：Cambridge University Press，1997.

[8] TAVIS M，CUMMINGS F W.Exact solution for an n-molecule-radiation-field Hamlitonian[J].Phys Rev，1968，170（2）：379-384.

[9]TESSIER T E，DEUTTSCH I H，DELGADO A.Entanglement sharing in the two-atom Tavis-Cummings model[J].Phys Rev A，2003，68（1）：25-35.

[10] ZHANG JIANSONG，CHEN AIXI，ABDELATY M.Two atoms in disspative cavities in di-spersive limit：entanglememt sudden death and long-lived entanglement[J].J Phys B：At Mol Opt Phys，2010，43（2）：501-508.

[11] XU J B，ZOU X B.Dynamic algebraic approach to the system of a three-level atom in the Λ configuration[J].Phys Rev A，1999，60（1）：4743-4751.

[12] WOOTTERS W K.Entanglement of formation of an arbitrary state of two qubit[J].Phys Rev Lett，1998，80（2）：2245-2252.

[13]COFFMAN V，KUNDU J，WOOTTERS W K.Distributed entanglement[J].Phys RevA，2000，61（2）：556-561.

[14] ZHANG J S，XU J B，LIN Q.Controlling entanglement sudden death in cavity QED by classical driving fields[J].The Europeeun Physical Journal：D，2008，51（2）：283-288.