公路貨物運輸量灰色馬爾可夫預測模型*
張文會 崔淑華 鄧紅星
(東北林業大學交通學院 哈爾濱 150040)
公路貨物運輸量預測既是道路運輸業發展調研的重要內容,又事關全國和區域道路運輸長遠發展規劃,其預測值是制定道路運輸業發展戰略的重要基礎數據.查閱文獻,對公路貨物運輸量的預測方法很多,隨著計算機的應用以及數據處理方法的發展,近年來主要有系統動力學模型[1]、BP神經網絡模型[2]、灰色系統模型[3]、支持向量回歸機模型[4]、馬爾可夫模型[5]以及混沌模型[6]等.預測方法直接影響預測精度,因此預測模型的選擇將關系到預測值的可行性與實用性.
本文基于灰色系統理論,在GM(1,1)預測方法的基礎上,引入馬爾可夫預測理論,建立灰色馬爾可夫預測模型,并以實例說明所建模型對公路貨運量和周轉量的預測精度.
1 GM(1,1)模型
設 時 間 序 列 X(0)有 n 個 觀 測 值:X(0)={X(0)(1),X(0)(2),…,X(0)(n)},要求n≥4.通過累加生成了新序列:X(1)={X(1)(1),X(1)(2),…,X(1)(n)}.
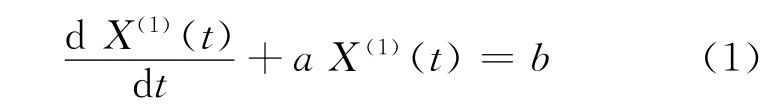
式中:a為發展灰數;b為內生控制灰數.
運用最小二乘估計以及微分方程理論得到GM(1,1)預測模型如下
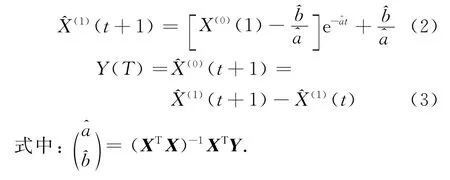
可以證明,原始非負序列X(0)作一次累加生成的序列X(1)具有近似的指數規律,稱為灰指數律.所以把生成序列X(1)視為t的連續函數,建立如下微分方程
2 灰色馬爾可夫預測模型
灰色馬爾可夫預測模型是將灰色系統理論和馬爾可夫鏈理論相結合建立的預測模型,既解決了灰色模型對波動較大的數據樣本預測精度不高的缺陷,又彌補了馬爾可夫模型要求數據具備平穩過程的局限性.
2.1 狀態劃分
對于一個具有馬爾科夫鏈特點的非平穩隨機序列Y(t),將其劃分為n個狀態,任一狀態區間表示為
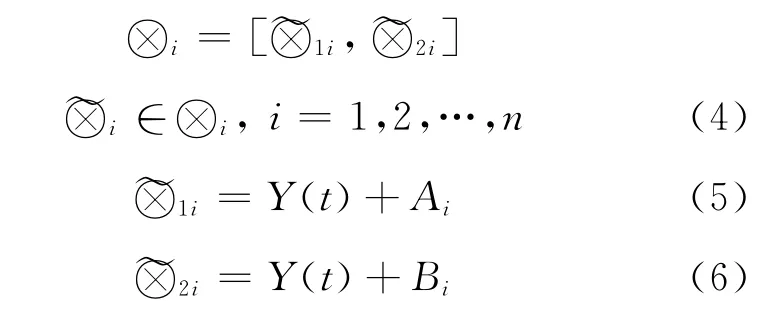
由于Y(t)是時間t的函數,因而灰元~?1i,~?2i也隨時間變化而變化,即狀態?i具有動態性.
狀態劃分數量與樣本數及擬合的誤差范圍有關,若過多則需要樣本較多,過小則狀態差別不明顯,失去了對波動調整的意義.一般以3~5為宜[7].
2.2 狀態轉移概率
1)狀態轉移概率
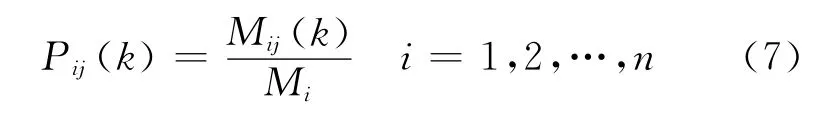
2)狀態轉移矩陣
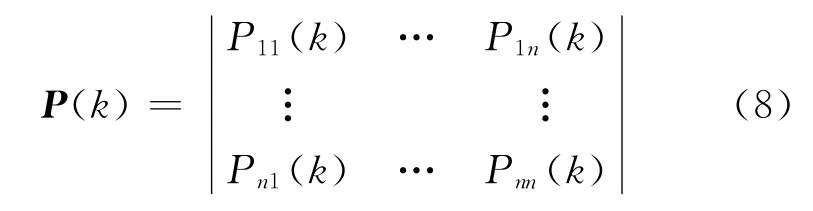
式中:Mij(k)為由?i狀態經過k步轉移到?j狀態的原始數據樣本數;Mi為處于?i狀態的原始數據樣本數;Pij(k)為相關參數由?i狀態經k步轉移到?j狀態的概率.
狀態轉移概率矩陣描述了系統各狀態轉移的全部統計規律,在實際運用中,一般只要考查一步轉移概率矩陣P(1),設預測時相關參數處于?k狀態,則考察狀態轉移概率矩陣第k行,若
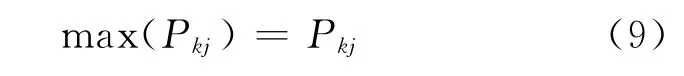
則可認為下一時刻系統最有可能由?k狀態轉向?l狀態.若遇矩陣中第k行有2個或者2個以上概率相同或相近時,則狀態的未來轉向很難確定,此時需要考察兩步或n步轉移概率矩陣P(2)和P(n)(其中n≥3).
當狀態劃分不太適合,以致某一狀態中無原始數據落入時,則可令Pij(k)=Pji(K)=0.由此,可求出狀態轉移概率矩陣(TPM)R(m)來預測未來狀態的轉向.
3)k步狀態轉移概率.經過k步轉移由狀態?i轉移到狀態?j的概率記為
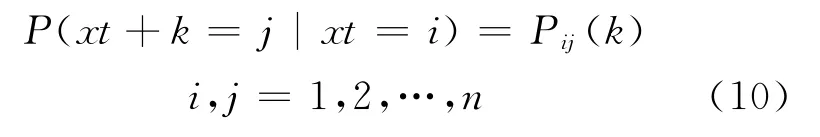
當系統滿足穩定性假設時,k步狀態轉移概率為

式中:P為一步狀態轉移矩陣.
4)灰色馬爾可夫預測模型.當確定了數據樣本未來狀態轉移概率矩陣后,也就確定了未來時刻相關參數的變動灰區間,可以用區間中位數作為未來時刻的預測值G(t),即
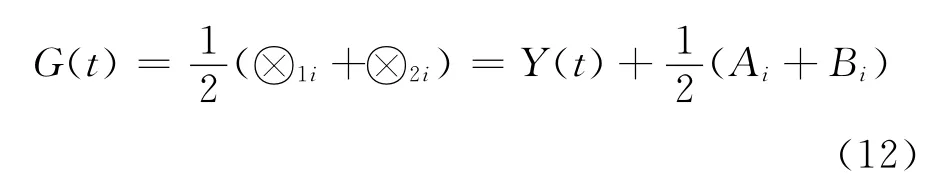
3 公路貨物運輸量預測實例
以黑龍江省1978~2008年公路貨運量和貨運周轉量作為基礎數據,見表1.
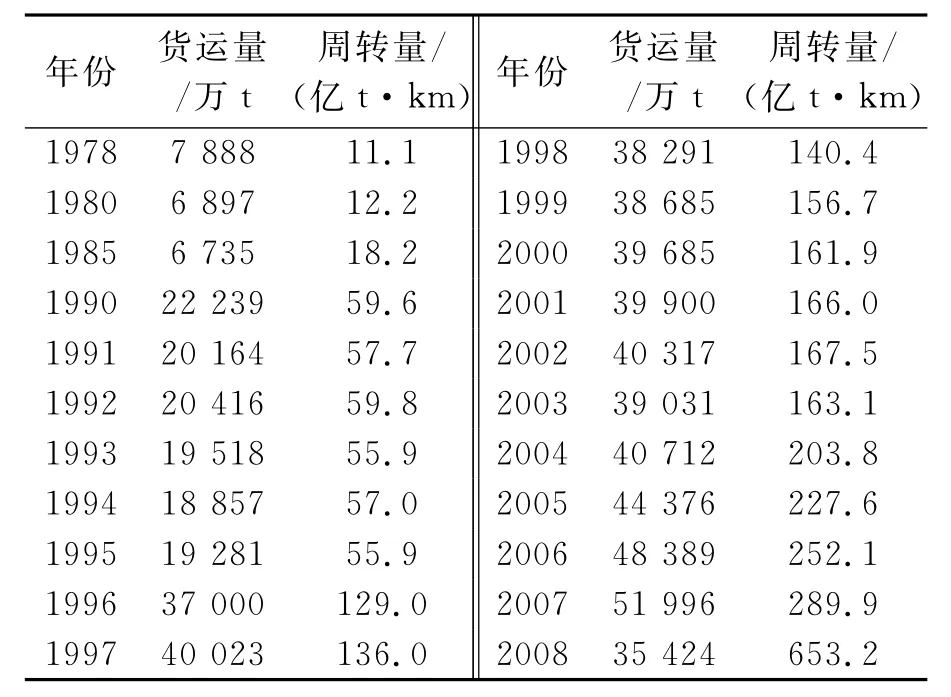
表1 公路貨運量和貨運周轉量數據
3.1 貨運量預測
1)貨運量GM(1,1)模型 由表1數據建立如下貨運量的GM(1,1)模型:
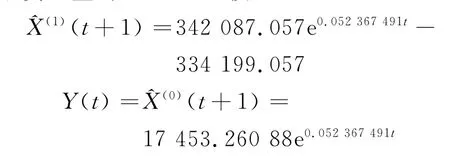
2)模型精度檢驗 計算原始數據序列的標準差,殘差序列的標準差,后驗差比值以及小誤差概率,進行模型精度檢驗,計算所得結果見表2.

表2 貨運量GM(1,1)模型精度檢驗
查找灰色預測模型精度檢驗等級表[8],貨運量的GM(1,1)預測模型后驗殘差比值雖為一級,但小誤差概率為三級,勉強合格,需用馬爾可夫預測模型修正.
3)狀態劃分 由表1原始數據,將貨運量原始數據劃分為4個狀態,即n=4:
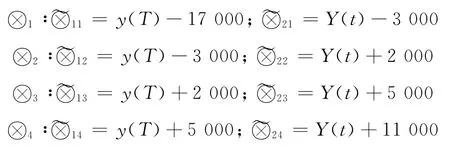
式中:Y(t)為t時刻貨運量GM(1,1)模型預測值.4)計算狀態轉移概率 由表1原始數據以及上述狀態劃分,可得到貨運量的一步狀態轉移概率矩陣
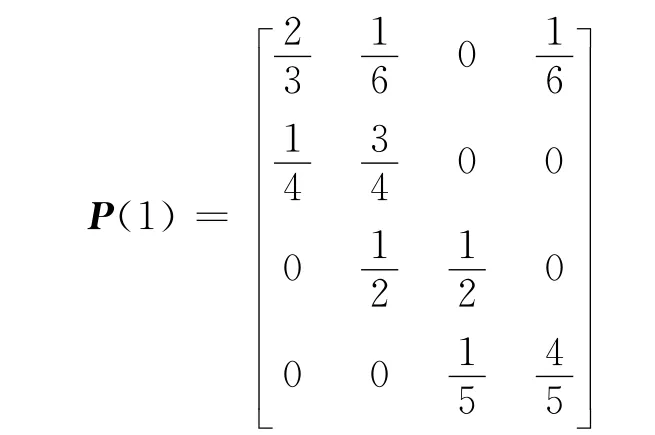
5)貨運量預測.由以上狀態轉移概率矩陣可以預測未來貨運量,由表1知2004年的貨運量處于狀態?2,則根據狀態轉移概率確定方法,考察狀態轉移概率矩陣的第2行,可看出
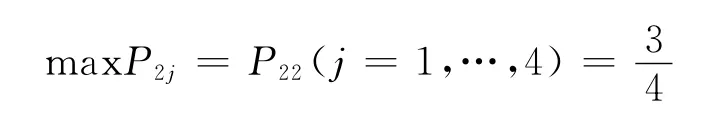
經過1 a的轉移,2005年的貨物周轉量最有可能處于狀態?2,根據式(2)和(3)以及式(12),2005年貨運量預測值為
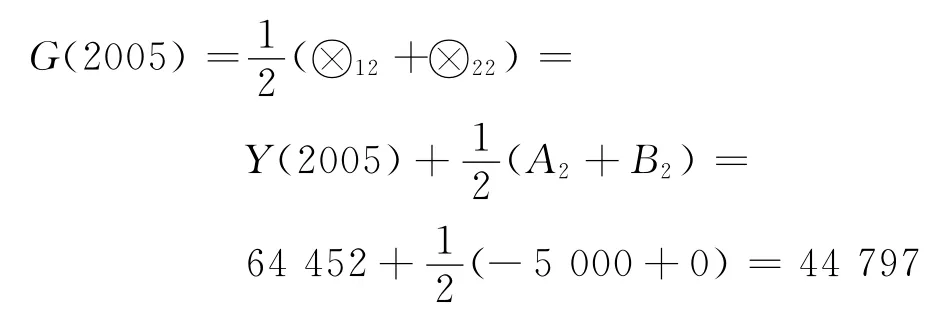
同理可以預測2006~2008年的貨運量.表3為2005~2008年貨運量灰色預測結果與灰色馬爾可夫預測結果的比較.
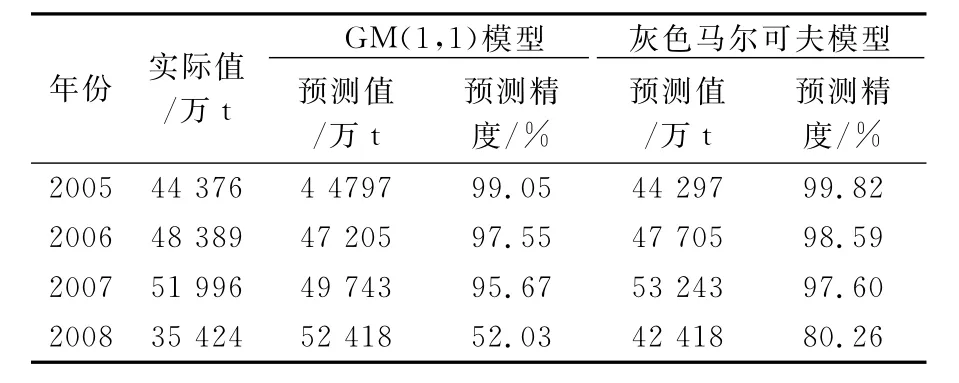
表3 貨運量預測比較
由表3可見,貨運量灰色馬爾可夫預測模型的預測精度高于GM(1,1)模型.可預測2015年黑龍江省公路貨運量為:G(2015)=65 627萬t.
3.2 貨運周轉量預測
與貨運量預測過程相似,灰色馬爾可夫預測模型也可預測貨運周轉量,見表4.
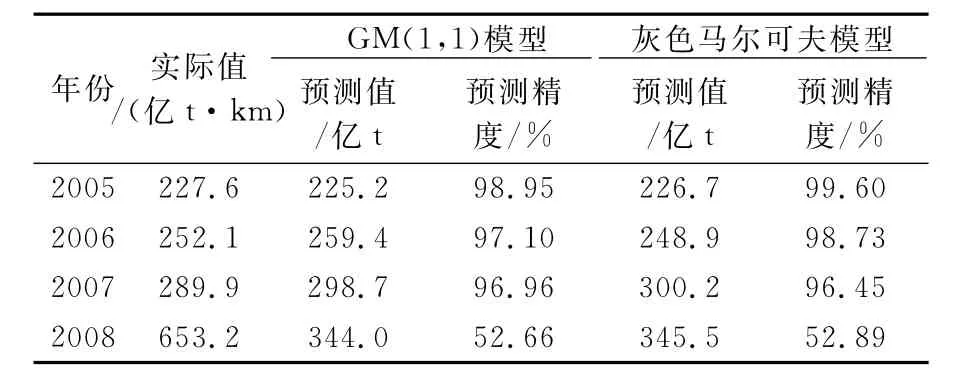
表4 貨運周轉量預測比較
由表4可見,貨運周轉量灰色馬爾可夫預測模型的預測精度高于GM(1,1)模型.可預測2015年黑龍江省公路貨運周轉量為:G(2015)=925.6億t·k m.
4 結束語
交通運輸體系是一個多因素、多層次、多目標的復雜系統,其中公路貨物運輸量受多指標因素的影響,具有明顯的層次復雜性,結構關系具有模糊性,發展變化具有隨機性,因此單一預測模型很難保證預測精度.灰色模型不適合長期的、隨機和波動性較大的數據序列,馬爾科夫模型適合描述隨機波動性較大的預測模型.本文將灰色模型和馬爾科夫模型結合,構建灰色馬爾科夫預測模型.按特定的狀態劃分方法,先用灰色模型預測,再用馬爾科夫模型對預測結果進行優化.將灰色馬爾科夫模型用于黑龍江省公路貨物運輸量預測,精度比GM(1,1)模型高.目前對原始數據序列的狀態劃分尚無統一標準,本文將原始數據序列劃分為4個狀態,對多狀態劃分的預測模型以及預測精度應進一步深入研究.
[1]王云鵬,楊志發,李世武.基于系統動力學的道路運輸量預測模型[J].吉林大學學報:工學版,2005,35(4):426-430.
[2]趙淑芝,田振中,張樹山.基于BP神經網絡的組合預測模型及其在公路運輸量預測中的應用[J].交通運輸系統工程與信息,2006,6(4):108-112.
[3]鄢勇飛,朱順應,王 紅.基于 灰色系統的公路運輸量預測方法[J].武漢理工大學學報:交通科學與工程版,2010,34(1):93-96.
[4]黃 虎,嚴余松,蔣葛夫.基于支持向量回歸機的公路貨運量預測模型[J].計算機應用研究,2008,25(2):632-636.
[5]王金艷.加權馬爾可夫模型在公路貨運量預測中的應用[J].數學的實踐與認識,2009,39(9):162-167.
[6]谷遠利,曲大義,于 雷.公路運輸貨運量預測方法研究[J].物流技術,2008,27(3):36-38.
[7]劉次華.隨機過程及其應用[M].3版.北京:高等教育出版社,2004.
[8]劉思峰,郭天榜,黨耀國.灰色系統理論及其應用[M].北京:科學出版社,1999.

