Boussinesq方程新的精確解
楊瓊芬 杜先云 楊立娟
(綿陽師范學院數學與計算機科學學院 綿陽 621000)
0 引 言
隨著非線性科學技術的不斷發展,非線性科學理論的研究問題在自然科學和社會科學領域當中正在蓬勃發展.構造非線性發展方程精確解是孤立子理論的重要研究課題之一.目前,人們已經發現了很多有效的求解方法,如雙曲正切函數法[1],齊 次 平 衡 法[2],試 探 函 數 法[3],輔 助 方 程法[4],EXP-函數展開法[5]等.
試探函數法是一種行之有效的用于求解非線性偏微分方程的方法,本文利用函數變換與雙線性算子相結合的方法,構造Boussinesq方程新的精確解.
經典的Boussinesq方程形如
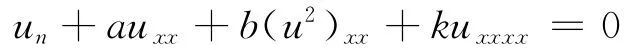
式中:u(x,t)為流體自由表面的運動;正常數a,b依賴于流體的深度和長波的特征速度.
Boussinesq方程是一種能夠描述規則波和不規則波在復雜地形上發生淺化、折射、繞射和反射效應相當有效的數學模型.1871年Boussinesq考慮垂向流速及壓強分布的影響,假定垂向流速從底面零線性增加到自由表面的最大值,得到了Boussinesq方程.考慮波浪傳播的非線性變化,1967年Peregrine推導了變水深條件下淺水區波浪傳播的Boussinesq方程.后來Boussinesq方程也適用于其他的物理應用中,如等離子體中的離子聲波等,由于它可以用來描述2個相反方向傳播的Kdv孤波,也可以描述一維非線性晶格的振動[6],因此,Boussinesq方程的研究受到許多學者的關注[7].
1 Boussinesq方程的精確解
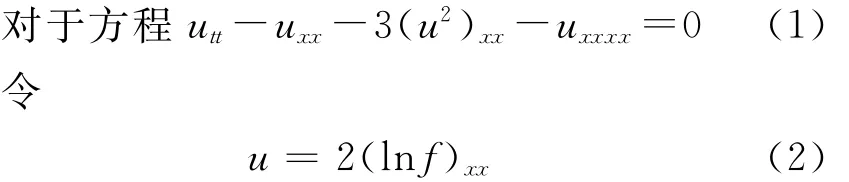
式中:f為待定函數.
將式(2)代入式(1)成雙線性形式


再將f(x,t)代人式(2)得到原方程(1)的大量的新的精確解,包括實數解,復數解為u(x,t)=
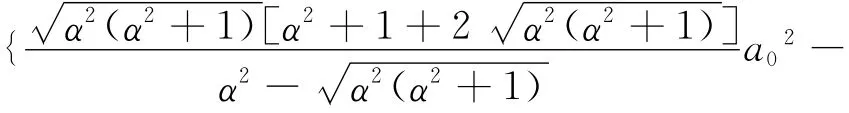

即得到原方程的一個新的通解.
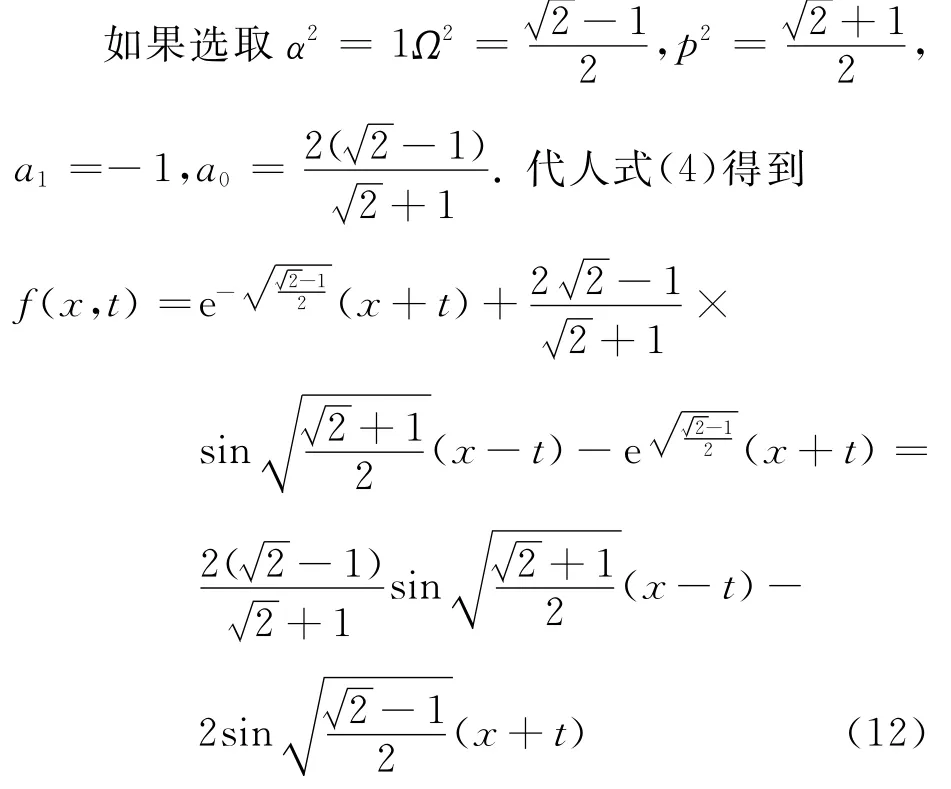
再將式(12)代人式(2)得到原方程的一個精確解為
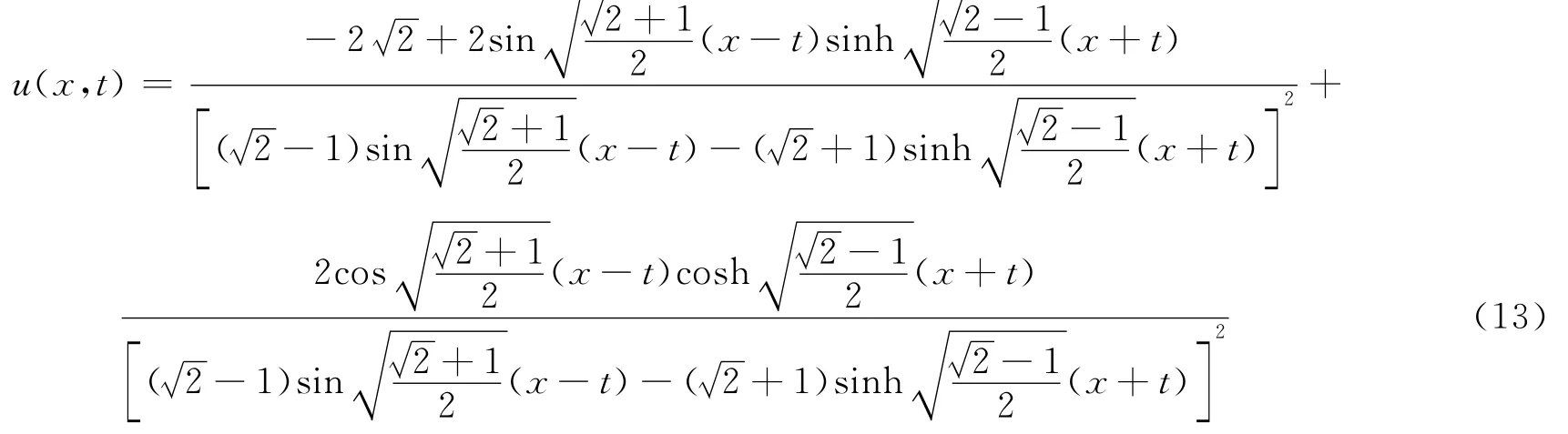
為了對解的結構有一個清楚的認識,借助于Maple,畫出了解式(13)對應的解的波形圖如圖1所示.
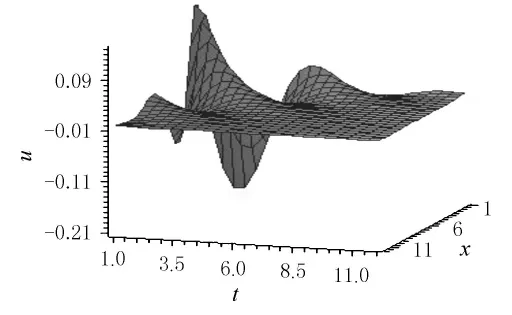
圖1 解式(13)對應的解的波形圖
2 結束語
根據齊次平衡原則,試探函數法并利用雙線性形式求出了Boussinesq方程一些精確解,包括實數解,復數解.當參數取不同的值,可以得到不同形式的新的精確解.在利用試探函數法時引進了新的函數,且采用了雙線性形式使式子看起來更為簡單.其解都是新解,且這些解對于解釋一些物理現象有一定的意義.
[1]Parkes E J,Duffy B R.An automated tanh-function method for finding solitary wave solutions to nonlinear evolution equation[J].Comp.Phys.Commun,1996,98:288-300.
[2]Wang Mingliang.Solitary wave solutions for variant Boussinesq quations[J].Phys.Lett.A,1995,199:69-172.
[3]Kudryashow N A.Exact solutions of the generalized Kuramoto-Sivashinsky equations[J].Phy.Lett.A ,1990,147(5-6):287-291.
[4]Sirendaoreji,Sun J.Auxiliary equation method for solving nonlinear Partial differential equation[J].Phys.Lett.A,2003,309:387-396.
[5]He J H,Wu X H.Exp–function method for nonlinear wave equations[J].Chaos Solitons Fract ,2006,30:700-708.
[6]Deift P,Tomei C,Trubowitz E.Inverse scttering and the Boussinesq equation[J].Pure Appl Math,1982,35(5):567-628.
[7]吳勇旗.(2+1)維Boussinesq方程的新的周期解[J].物理學報,2008,57(9):5390-5394.

