小波在結構損傷鑒定中的應用

楊海鳴 楊 帆

（深圳地鐵集團有限公司1） 深圳 518026）（同濟大學結構工程與防災研究所2） 上海 200092）

近來被譽為分析信號的數學顯微鏡的小波變換［1］，以其在信號處理方面的強大功能，正被逐步引入到結構健康診斷中.利用模態測試識別模態參數是進行結構健康診斷的有效方法，而將小波變換應用到結構模態參數［2］上（例如模態振型），對結構進行損傷檢測，為結構健康診斷開拓了一個新的研究領域.由于Fourier變換缺乏空間局部性［3－4］，因此由函數的Fourier變換只能確定其奇異性的整體性質而難以確定其奇異性的空間分布情況.也就是說當函數有許多奇點時，用Fourier變換難以確定各奇點的位置及各奇點奇異性的強弱.

1 信號奇異性與小波模極大值的關系

小波變換除了可以寫成的內積形式以外，還可以寫成卷積形式［5－6］，它們在本質上是一樣的.下面列出卷積形式：

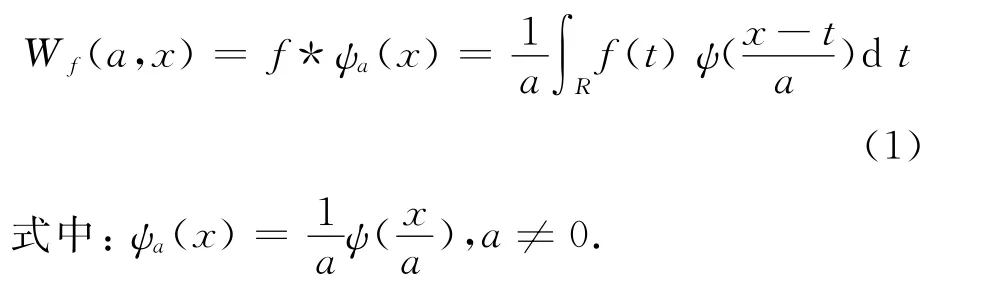
設h（t）是函數f（t）和g（t）的卷積，則根據傅里葉變換的性質有

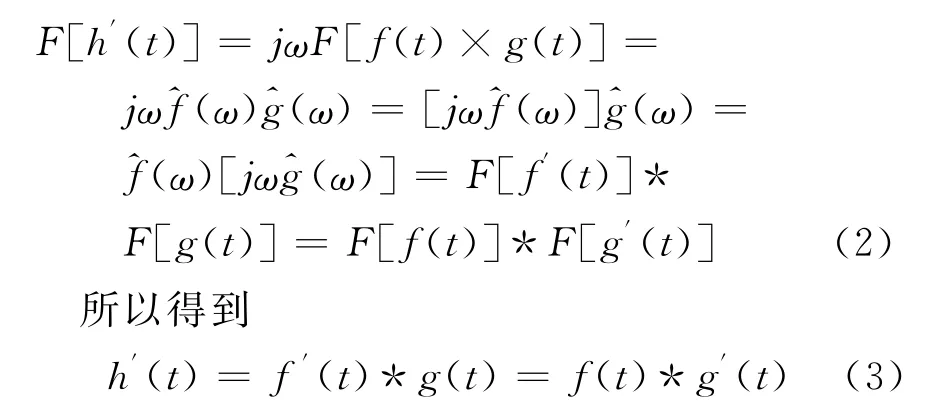
若將函數f（t）看做是信號，g（t）看做是濾波器，那么，信號的導數與濾波器的卷積結果可看成是濾波器的導數與信號的卷積.例如，如果選g（t）為高斯函數，則利用其導數可以構造Morlet小波和Maar小波，因此，小波變換的突變點和極值點與信號f（t）的突變點和極值點具有對應關系，利用小波變換可以檢測突變信號.具體過程如下.

設θ（t）是一個起平滑作用的低通平滑函數，且滿足條件為

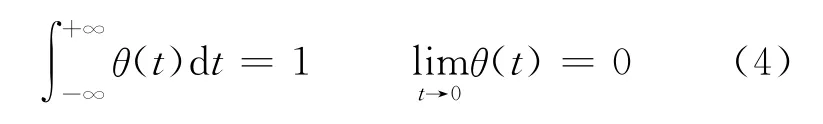
通常θ（t）取為高斯函數，即

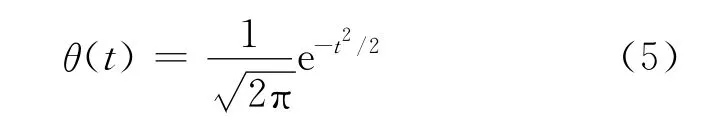
假設θ（t）是二次可導的，并且定義為

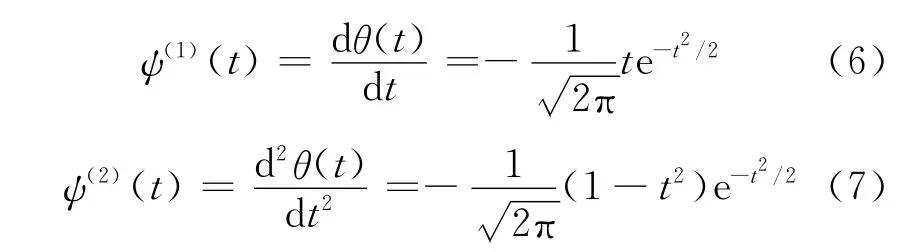
則函數ψ（1）（t），ψ（2）（t）滿足小波的容許條件，即

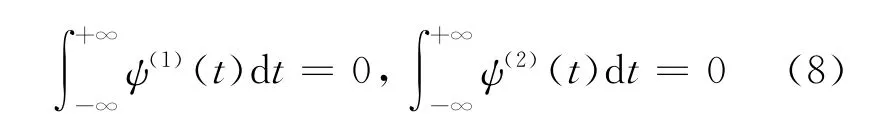
因此，可用為小波母函數.

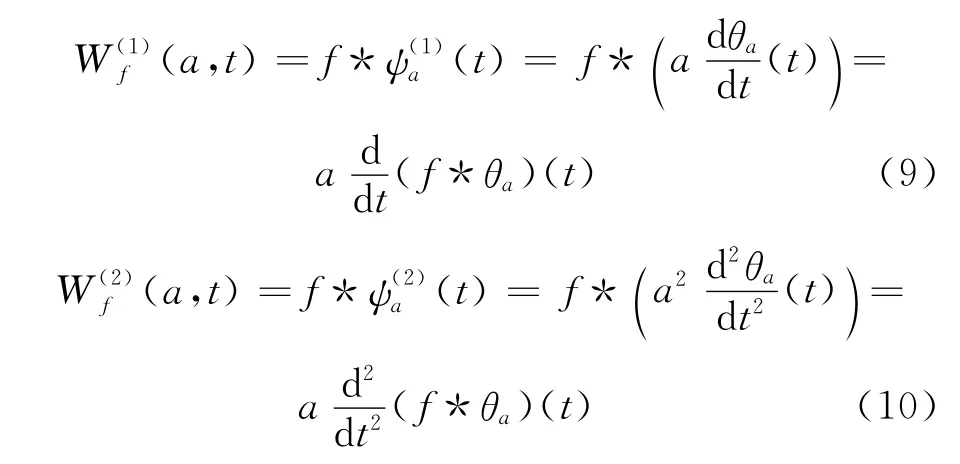
由于階躍函數的導數是脈沖函數，脈沖函數的導數是零.如果信號中存在階躍型奇異點，當小波函數可看做某一平滑函數的一階導數時，就會在該點產生小波變換模的局部極值點.當小波函數可看做某一平滑函數的二階導數時，信號小波變換模的過零點，這就是采用檢測小波變換系數模的過零點和局部極值點可檢測信號的突變點的原理.

由上面敘述可知，要想使信號的不同類型奇異點經過小波變換后得到過零點或是局部極值點需要針對不同的奇異點類型選用不同的小波，其主要原則是看小波是光滑函數的幾階導數.文獻［7－8］中介紹了一個非常有用的定理：快速衰減的小波ψ具有n階消失矩，當且僅當存在快速衰減函數θ使得此時的小波變換為可見如果小波函數是平滑函數的n階導數那么它的消失矩就是n.

2 信號奇異性指數和小波模極大值的關系

將離散母函數ψj，k（t）改寫為

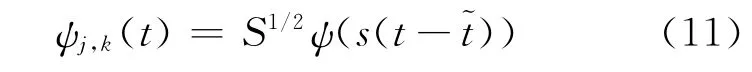
式中：s＝2j；~t在ψj，k（t）的支集內.

于是j尺度下的小波變換的模可表示為此式方括號中權是有界量，故有

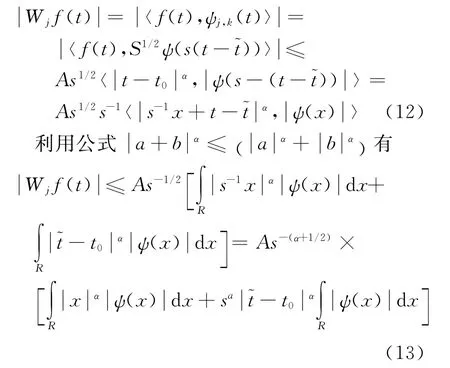
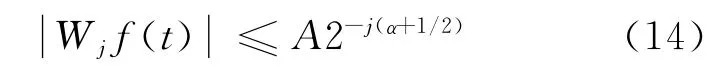
因為a＝2－j所以還有式

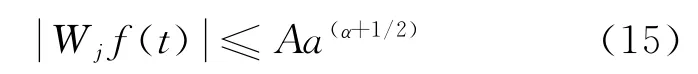
當小波平移到奇異點時，取等號.

由上式可知小波變換模極大值大小隨尺寸變化的規律：（1）若α＜0，例如在δ函數或尖峰函數的突變點處，隨著j值得增大（尺寸變細），將越來越大.對于白噪聲信號來說，因為它是隨機的、且是密集地逐點滴類似于δ函數形的，所以其指數α＜0，其小波變換幅值也是隨j值增大而增大且是密集的；（2）若α＝0，例如在階躍函數突變點，不隨尺寸的改變而變化；（3）若α＞0，例如在折線突變點處，隨著j值增大（尺寸變細），越來越小.

檢索并保留突變點t0處不同層的小波變換模極大值，標記如下.

應該看到，在較細尺度層上作上述估計才是較準確的，在多個較細尺度層上作上述估計可獲得較穩定的結果.

3 結構損傷分類

設w為平面結構豎向位移，結構的轉角、彎矩和剪力可以表達為

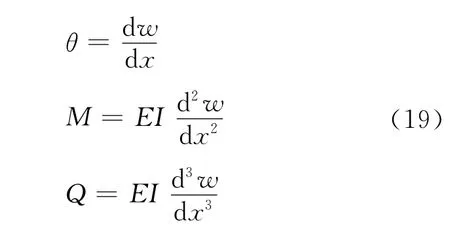
完整結構在任何受力狀態下，位移、轉角都是連續的；當結構上沒有集中力偶作用時，無論結構完整與否，彎矩都是連續的；當結構上沒有集中荷載作用時，無論結構完整與否，剪力也應該是連續的，但是由于這種受力狀態（結構上不受集中荷載）在工程中非常少見，不具備普遍性，所以可以認為結構中的剪力本身是不連續的.取結構上任意一點x＝a，有如下連續性表達式

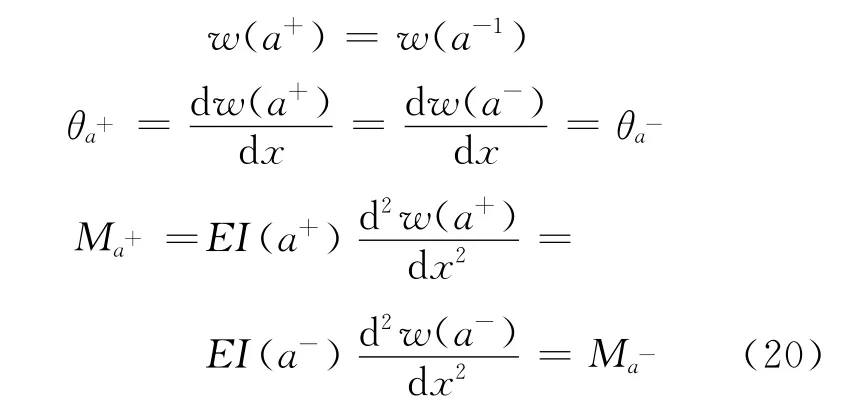
如果信號產生了損傷，那么其位移信號將會在損傷點產生奇異性，針對對位移信號奇異性的幾種分類，下面指出其對應的結構損傷類型：

1）如果位移信號在a點不連續，即w（a＋）≠w（a－）.對于2種不連續情況，如果位移發生了階變型突變，相當于結構在a點錯動.如果位移發生了尖峰型突變，相當于結構在a點起拱.

2）如果位移信號一階導數在a點不連續，這相當于轉角信號不連續，此時即對于2種不連續情況，如果位移信號一階導函數發生了階變型突變，相當于結構在a點發生整體轉動.如果位移信號一階導函數發生了尖峰型突變，相當于結構在a點結構在a點發生局部轉動.

綜上，可以將結構的損傷形式歸結為4類：起拱、錯動、局部剛度衰減及整體剛度衰減.由階變型和尖峰型的導數關系可知，高階的尖峰型突變實際上是降一階的階變型突變，所以與結構損傷類型相對應的位移信號奇異性為：位移發生了突變和階變、位移的二階導數發生突變和階變.

4 實例分析及討論

利用懸臂梁縱向位移信號和縱向位移差信號對4種損傷類型進行奇異性檢測，主要比較兩種方法在形成模極值點、模峰值點、以及奇異點最終定位上的效果，同時研究模極值點分布規律以便對奇異點定位作輔助判斷.對于簡單結構其第一階振型和位移十分相似，可以用振型信號代替位移信號.

基本參數 模擬一懸臂梁，其基本數據為：梁長5 m，寬0.4 m，高0.4 m，材料密度ρ＝7 800 kg／m3，泊松比υ＝0.2，梁完好時彈性模量E＝2×1011Pa.將梁身劃分為100個單元，101個節點，對50號單元以后的所有單元彈性模量加以修改，分別改為E＝2×1010Pa和E＝1×1011Pa，得到一階振型圖如圖1、圖2所示.

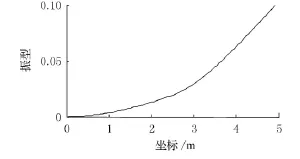
圖1 52號節點剛度強突變

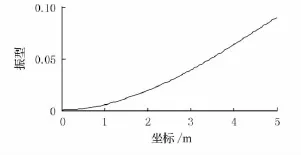
圖2 52號節點剛度弱突變

本文采用gaus3小波.對圖1示信號作小波變換，并提取其模極大值，畫出在尺度1～8上小波模極大值分布圖，見圖3.

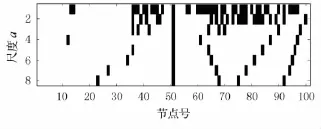
圖3 圖1所示信號模極大值分布（尺度a為1～8）

利用guas3小波，對圖1所示信號和無損信號之差作小波變換（尺度a從1～8），并提取其模極大值，畫出在尺度1～8上小波模極大值分布圖，見圖4.

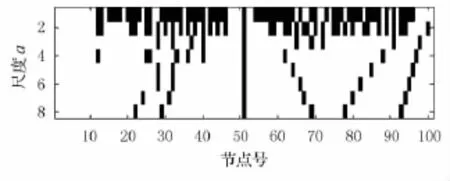
圖4 圖1所示信號差模極大值分布（尺度a為1～8）

利用gaus3小波對圖2所示信號作小波變換，并提取其模極大值，畫出在尺度1～8上小波模極大值分布圖，見圖5.

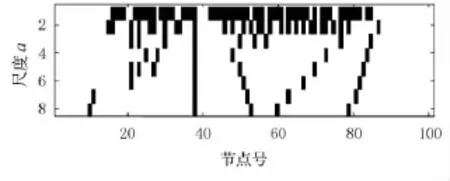
圖5 圖2所示信號模極大值分布（尺度a為1～8）

利用guas3小波，對圖2所示信號和無損信號之差作小波變換（尺度a從1～8），并提取其模極大值，畫出在尺度1～8上小波模極大值分布圖，見圖6.

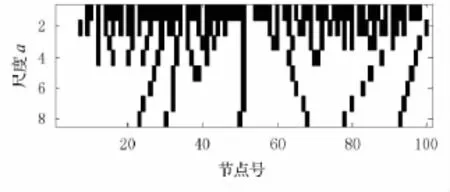
圖6 圖2所示信號差模極大值分布（尺度a為1～8）

從圖3～6可見利用模極大值分布圖來辨別奇異點，從圖中可以看出在尺度8以內，51號節點處能夠形成一條不偏移的模極大值線（豎線）.因為是50號單元損傷所以損傷點出現在51節點是非常精確的.模極大值分布是確定損傷位置的最佳方法.

5 結 論

1）為方便計算，選用的比較簡單的小波，而所選小波的不同肯定會引起合成地震動的時頻特性的不同，如何針對不同的工程要求，選擇最佳的小波是基于小波的地震動合成研究中的一個非常重要的課題.

2）本文提到了信號降解方法，并得出結論有損信號和無損信號差是對梁結構的一種有效的降解方法，但這種方法是特定的，針對不同的結構，不同的奇異性類型尋找新的降解方法將是小波探傷研究中的另一個重要課題.

3）利用小波模極大值的分布可以更加清晰的判定損傷位置.

［1］陳長征.結構損傷監測與智能診斷［M］.北京：科學出版社，2001.

［2］Doebling S W.A su mmar y review of vibration－based damage identification methods［J］.The Shock and Vibration Digest，1998，30（2）：91－105.

［3］Yun C B，Bahng E Y.Substructural identification using neural networ ks［J］.Co mputers and Str uctures，2000，77：41－52.

［4］Hou Z，Noori M，Amand R S.Wavelet－based approach for structural damage detectiom［J］.Journal of Engineering Mechnanics，2000，126（7）：677－683.

［5］Ovanesova A V，Suarez L E.Application of wavelet transfor ms to damage detection in frame structures［J］.Engineering str uctures，2004，26（1）：39－49.

［6］任宜春，李 峰，連續小波變換在梁結構損傷診斷中的應用研究［J］.振動、測試與診斷，2004，24（2）：122－124.

［7］唐和生，松 濤.基于小波變換在梁結構損傷診斷中的應用研究［J］.固體力學學報，2004，25（1）：47－52.

［8］郭 建，炳 南.基于小波變換的橋梁健康監測多尺度分析［J］.浙江大學學報：工學版 ，2005，39（1）：114－118.