基于偽并行改進遺傳算法的線列陣隔振系統參數優化

江國和,薛 峰

(1.上海海事大學商船學院,上海 200135;2.江蘇科技大學船舶與海洋工程學院,江蘇 鎮江 212003)

0 引 言

拖曳線列陣聲吶具有遠離拖船、噪聲低、可變深、可充分利用水文條件以及孔徑不受限制等優點,在現代反潛、海洋水文和資源勘探測量中,得到了越來越廣泛的應用和發展。拖曳線列陣隔振系統是1個復雜的非線性系統,影響其隔振性能的參數有很多。所以需要合理選擇隔振系統參數,必須進行參數優化設計。對于隔振系統的參數優化設計,由于模型復雜,影響參數太多,所以存在很大的難度。本文以大型有限元軟件Ansys為工作平臺,利用其參數化設計語言(APDL)實現了偽并行改進遺傳算法對隔振系統的材料參數(充油密度、護套彈性模量、隔振組件彈性模量)的優化設計。

1 隔振系統模型和參數分析文件的建立

1.1 24m拖曳線列陣隔振系統二維流固耦合模型的建立

文獻[1]對水池中隔振系統在不同工況下的隔振量進行了實際測量,并對實驗數據進行了分析。文獻[2-3]分別建立了隔振系統流固耦合的二維和三維模型,對其隔振性能進行了分析。

圖1所示為劃分網格后的24 m線列陣隔振系統二維流固耦合模型局部圖,是包含2層流固耦合的模型,第1層是隔振系統護套內部充油和護套、隔振組件之間的耦合;第2層是隔振系統外部的水和整個隔振系統模型之間的耦合。二維流固耦合模型建立了隔振系統各部分結構沿軸向的剖面的平面模型,單元數為22850個,節點數為25470個。

圖1 24m隔振系統二維流固耦合模型局部圖Fig.1 24m two-dimensional fluid-structure coupling field model of VIS

選取激振力的幅值為25 N,拉力為1470 N。圖2給出了24 m線列陣隔振系統二維流固耦合模型所受拉力為1470 N時,通過模型計算出的隔振量[4]與實驗值的比較圖。

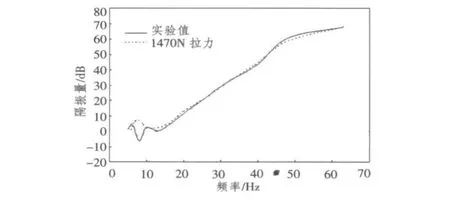
圖2 24m隔振系統二維流固耦合模型1470 N拉力時計算隔振量與實驗值的比較Fig.2 Compare experimental data with calculated of 24 m VIS in 1470N pulling force

由圖2可以看出,隔振效果的變化規律和水池實驗結果基本上是符合的,即在5～20 Hz的頻率范圍內隔振效果較差;在20～63 Hz的頻率范圍內,隔振效果隨激勵頻率的增大而增大。雖然定量上的數值還是有些出入,但是可以看出計算結果已經比較接近實驗值。通過模型計算與水池實驗結果的比較,可見,隔振系統二維流固耦合模型能較好地反映隔振系統的隔振性能。

1.2 24m拖曳線列陣隔振系統二維流固耦合模型參數分析文件的建立

24m隔振系統二維流固耦合參數化模型如圖3所示。在參數化模型的基礎上,進行1次完整計算和后處理過程,并讀取其命令流文件,進行修改,就得到了隔振系統優化參數的命令流分析文件。這個分析文件的建立也是隔振系統參數優化設計的基礎。

圖3 24m隔振系統二維流固耦合參數化模型Fig.3 24m two-dimensional fluid-structure coupling parametric model of VIS

2 偽并行改進遺傳算法在隔振系統優化設計中的應用

2.1 偽并行改進遺傳算法

基本遺傳算法在實際應用中存在以下幾方面的缺陷:1)對搜索空間變化的適應能力差。2)容易出現早熟收斂現象。3)算法在進化過程中由于采用隨機搜索的方法從而導致了收斂速度的下降。針對基本遺傳算法存在的缺陷,文獻[5]對遺傳算法提出了若干改進;文獻[6]提出1種自適應偽并行改進遺傳算法,并利用評價遺傳算法性能的2個典型測試函數:Ackley函數和De Jong函數F2,進行偽并行改進遺傳算法(PPIGA)和基本遺傳算法(SGA)性能的比較研究;文獻[7]利用偽并行改進遺傳算法解決了沖擊隔離系統限位器參數的優化設計問題。

偽并行遺傳算法的信息交換是在每代進化完成時,對每個子群體中的最佳個體按照一定的概率進行交換。由于這些子群體并未在不同的處理機上獨立進行,仍是在單臺微機上串行執行的故稱其為偽并行遺傳算法。

偽并行改進遺傳算法利用分班選擇策略,采用自適應個體交叉、變異概率結合并行計算思想,開發出來的偽并行改進遺傳算法不但有效地維持了群體的多樣性,明顯地克服了早熟的現象,而且以較快的收斂速度得到較好的最優解。設計與個體適應度相關聯的交叉、變異概率。采用式(1)和式(2)的交叉、變異概率能有效地保護當前種群中優良個體,同時也能產生出良好的新個體。

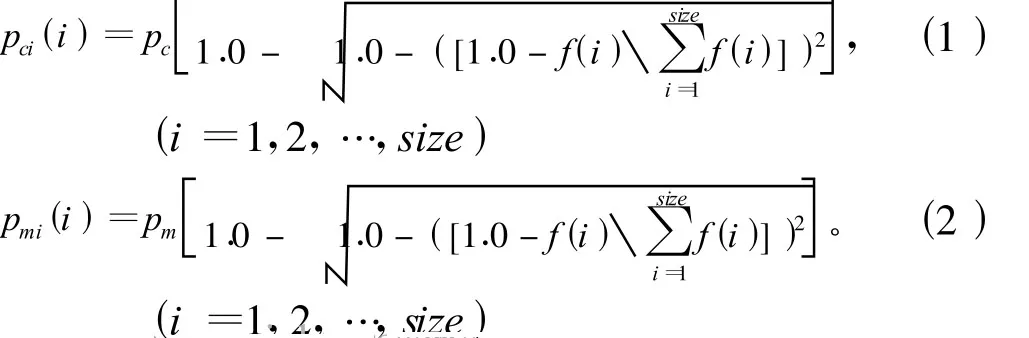
式中:f(i)為第i個個體的適應度;pc為交叉操作的概率;pm為變異操作的概率;p(i)為第i個個體被選中進行交叉或變異操作的概率。

2.2 拖曳線列陣隔振系統的優化設計

優化的隔振系統采用圖3所示的模型,為24 m隔振系統二維流固耦合模型。優化環境選取隔振系統所受拉力為1470 N,激勵力的幅值為25 N。

優化變量及其上下限分別是:充油密度600～900 kg/m3;護套材料的彈性模量1.0×106～1.0×109N/m2;隔振組件材料的彈性模量1.0×106～1.0×109N/m2。

優化目標是要求隔振系統在工作頻率20 Hz,32 Hz,40 Hz,48 Hz處的隔振量LdB的值最大。其數學模型描述如下:

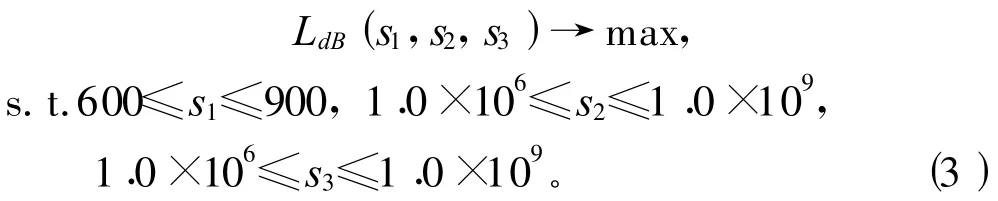
利用偽并行改進遺傳算法優化的具體過程如下:

1)解碼過程

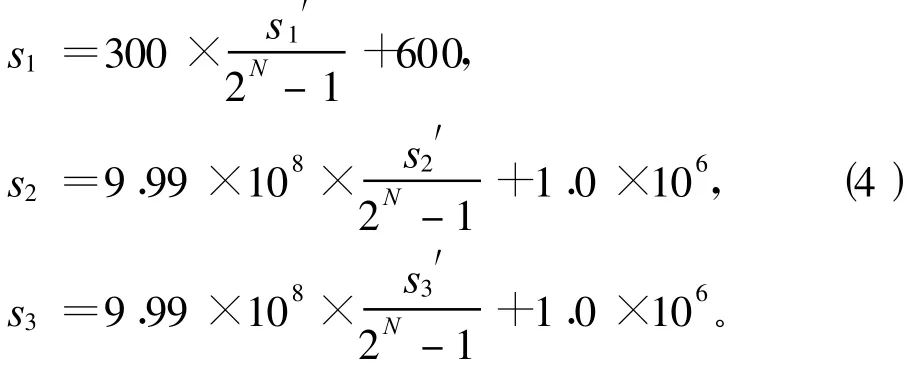
2)適應度計算

由于遺傳算法中的適應度為非負數,因此對于要求最大值的問題作如下變化:

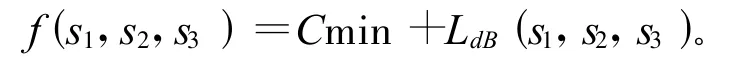
其中,Cmin為1個較小的常數,在此程序中設為0。

2.3 優化結果分析

利用偽并行改進遺傳算法對隔振系統中充油密度、護套材料彈性模量、隔振組件材料彈性模量進行優化,其中遺傳算法運行參數可選取個體長度length:10;子種群大小 popsize:50;最大運行代數maxgeneration:15;子群體數groups:3;交叉概率Pc:0.8;變異概率 Pm:0.05。

1)以20 Hz時的隔振量為優化目標的隔振系統的優化結果如圖4～圖7所示。其中圖4～圖6表示了24 m隔振系統中內部充油密度、護套彈性模量、隔振組件彈性模量的尋優過程。圖7表示目標函數即20 Hz時隔振系統隔振量的進化過程。當進化到9代時,目標函數基本上到達了最大值。

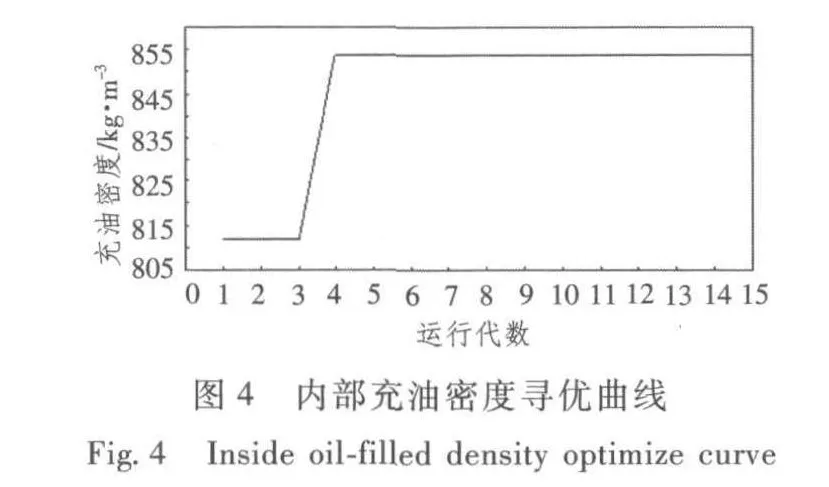
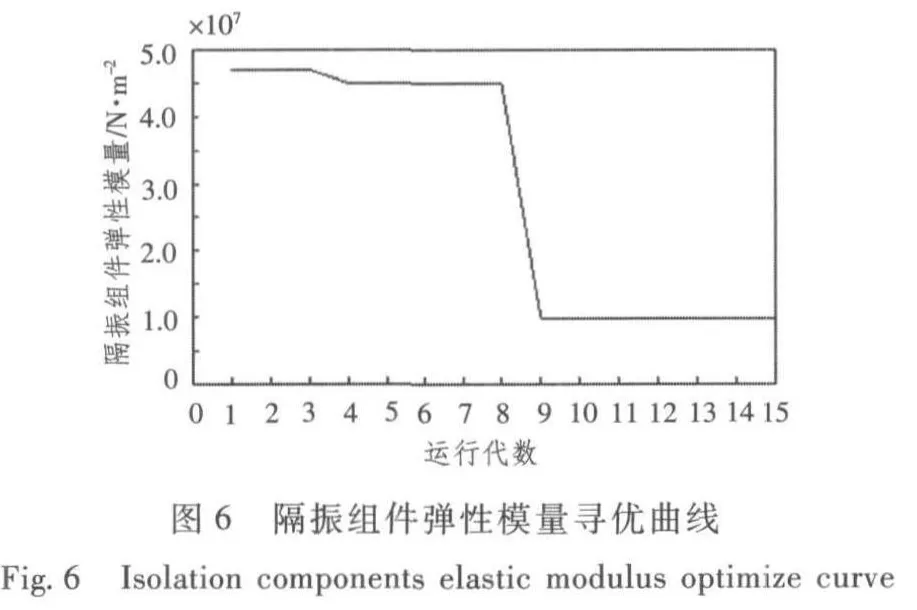
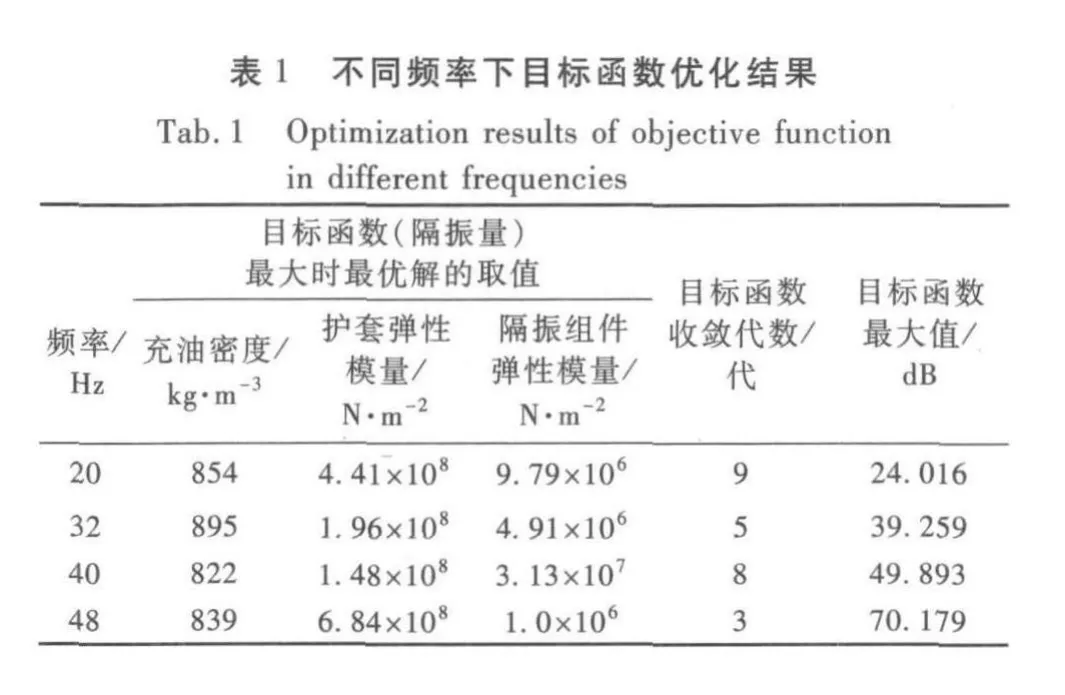
從計算結果可以看出,偽并行改進遺傳算法在第9代基本搜索到滿足要求的較好變量。由此可以得出對于此隔振系統在滿足20 Hz時隔振量最大時最優解為:內部充油密度的取值為854 kg/m3,護套彈性模量的取值為4.41×108N/m2,隔振組件的彈性模量的取值為9.79×106N/m2,此時隔振量為24.016 dB。

從圖7可以看出,在解的進化過程中,由于群體中適應度較低的一些個體逐漸被淘汰掉,而適應度較高的個體逐漸向最優解靠近,因此群體中最佳個體所對應的目標函數逐漸上升,在15代內得到全局最優解24.016 dB。

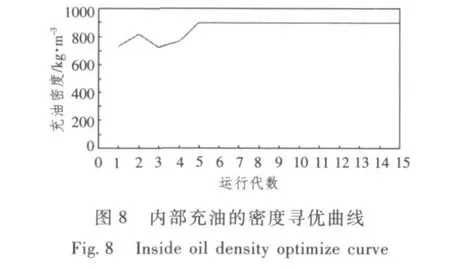
2)以32 Hz時的隔振量為優化目標的隔振系統優化結果如圖8～圖12所示。

3)以40Hz時的隔振量為優化目標的隔振系統優化結果如圖12～圖15所示。

4)以48 Hz時的隔振量為優化目標的隔振系統優化結果如圖16～圖19所示。

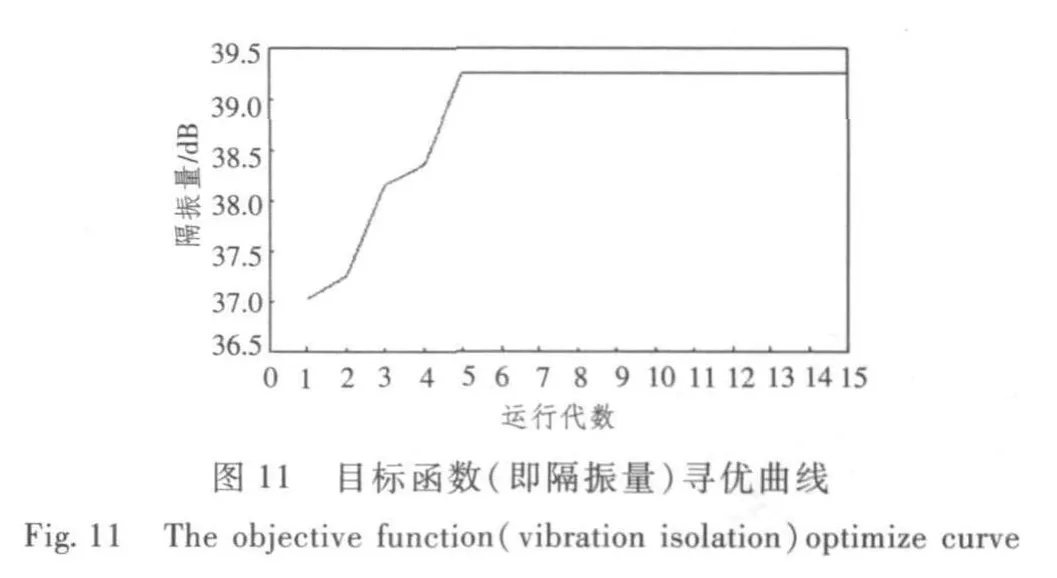
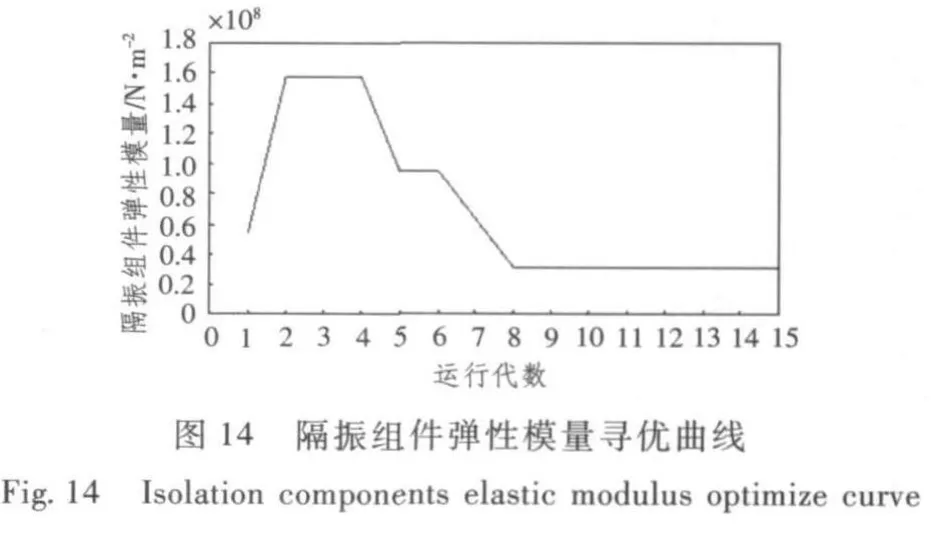
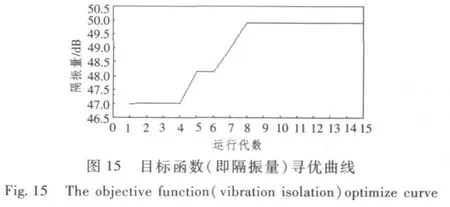
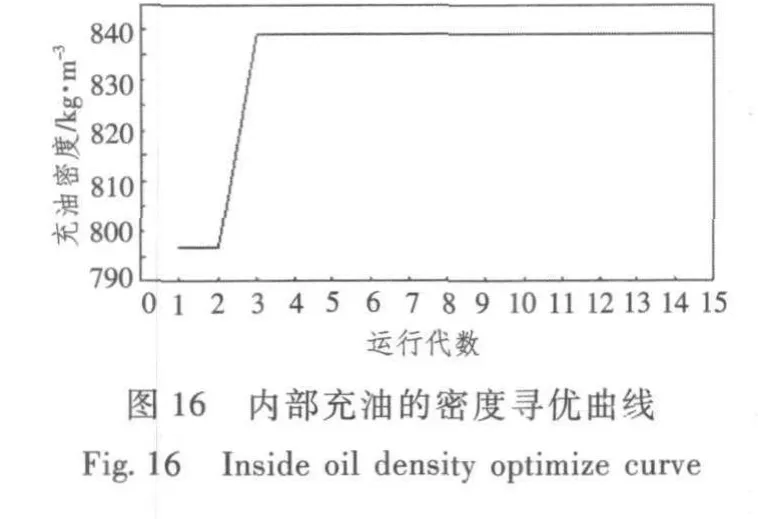
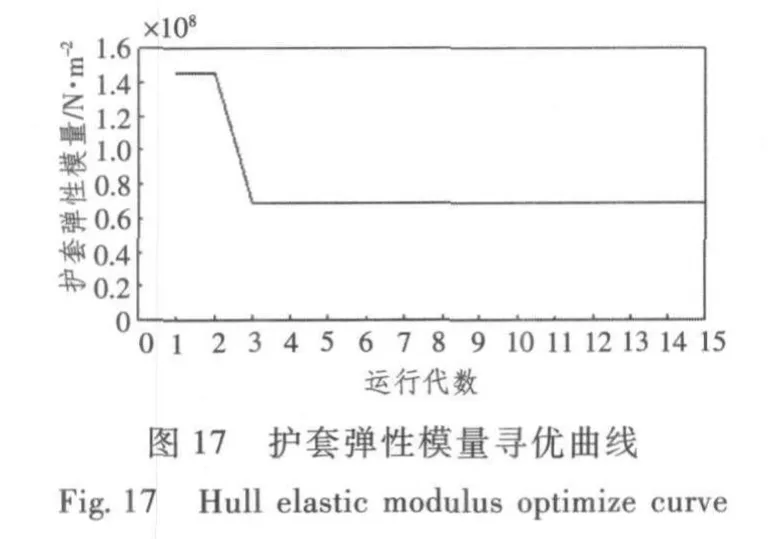
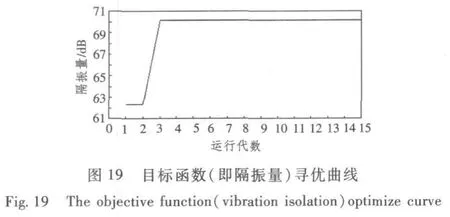
各個頻率下目標函數參數優化過程的結果見表1,從20 Hz,32 Hz,40 Hz和48 Hz頻率處的尋優曲線圖可以看出,偽并行改進遺傳算法以較快的收斂速度得到較好的最優解,在15代內基本搜索到滿足要求的較好變量,使得隔振量達到最大。隨著代數的增加參數值不再變化,約束條件均能得到滿足,因此可以確定此時的優化結果為優化參數的最佳值。

?

3 結 語

本文建立了24 m拖曳線列陣隔振系統的二維流固耦合模型,進行了隔振量計算分析,利用水池實驗結果對模型進行了驗證;基于參數化設計語言(APDL),建立了24 m線列陣隔振系統簡化的平面模型參數化分析文件。

通過Ansys的2次開發編寫了偽并行改進遺傳算法程序,實現了24 m線列陣隔振系統中內部充油密度、護套彈性模量、隔振組件彈性模量的研究和優化設計,并得出了一些相關的優化結果。通過計算結果表明,通過優化求得的隔振系統優化參數能滿足約束條件并實現隔振量最大化,這對線列陣隔振系統的優化設計具有重要的實際意義。

[1]江國和,王國治,洪有財,等.拖曳聲吶陣隔振模塊性能實驗分析[J].噪聲與振動控制,2003,24(3):45-48.

[2]江國和,孔曉麗.基于流固耦合模型的拖曳線列陣隔振模塊隔振性能分析[J].江蘇科技大學學報,2008,22(2):57-59.

[3]江國和,許影博.細拖曳線列陣隔振模塊隔振性能分析[J].江蘇科技大學學報,2009,23(4):293-296.

[4]嚴濟寬,柴敏,陳小琳.振動隔離效果的評定[J].噪聲與振動控制,1997,(6):22-30.

[5]周敏.遺傳算法的若干改進及應用[D].中國科學院軟件研究所,2001.

[6]張小華,江國和,沈榮瀛.一種自適應偽并行改進遺傳算法[J].華東船舶工業學報,2005,(3):69-73.

[7]江國和,張小華,等.基于偽并行改進遺傳算法的限位器參數優化[J].中國造船,2006,(04):24-31.