某越野車懸架下擺臂的結(jié)構(gòu)輕量化設(shè)計(jì)

嚴(yán) 君 楊世文 盧建志

中北大學(xué) 機(jī)電工程學(xué)院 030051

前言

現(xiàn)今社會(huì)，節(jié)能與環(huán)保成為汽車工業(yè)發(fā)展的主旨，汽車輕量化設(shè)計(jì)研究作為其中的重要課題越來(lái)越受到各方面的關(guān)注。傳統(tǒng)的汽車零部件的結(jié)構(gòu)材料以鋼板為主，已經(jīng)無(wú)法適應(yīng)人們對(duì)汽車高速與輕量化的追求。目前國(guó)內(nèi)外汽車結(jié)構(gòu)輕量化的研究方向主要集中在兩個(gè)方面：一是開發(fā)具有比模量和比強(qiáng)度高的輕質(zhì)高性能材料來(lái)替換原來(lái)的鋼板材料；二是采用結(jié)構(gòu)優(yōu)化技術(shù)設(shè)計(jì)出輕量化結(jié)構(gòu)來(lái)取代原有結(jié)構(gòu)[1]。

國(guó)內(nèi)外有關(guān)懸架擺臂的結(jié)構(gòu)優(yōu)化設(shè)計(jì)研究有桑楠，白玉等主要是利用ABAQUS軟件對(duì)某汽車的前擺臂進(jìn)行了有限分析，在此基礎(chǔ)上為了進(jìn)一步改善結(jié)構(gòu)的承載能力和降低結(jié)構(gòu)的質(zhì)量，提出了該擺臂結(jié)構(gòu)輕量化設(shè)計(jì)的方案[2]；王鳳軍，扶原放等提出了基于可靠性理論，以提高結(jié)構(gòu)的可靠性作為結(jié)構(gòu)優(yōu)化設(shè)計(jì)的目標(biāo)，結(jié)合有限元結(jié)構(gòu)優(yōu)化方法進(jìn)行某懸架下擺臂的輕量化設(shè)計(jì)研究[3]；張兆良則利用Hypermesh軟件進(jìn)行了某雙橫臂懸架上下擺臂的拓?fù)鋬?yōu)化分析和剛、強(qiáng)度分析，同時(shí)設(shè)計(jì)了上下擺臂的輕量化結(jié)構(gòu)[4]；祝小元，方宗德等提出了多工況下針對(duì)汽車懸架控制臂結(jié)構(gòu)進(jìn)行了以靜態(tài)柔度和低階振動(dòng)固有頻率的多目標(biāo)拓?fù)浣Y(jié)構(gòu)優(yōu)化研究，解決了靜態(tài)的擺臂剛度問題和動(dòng)態(tài)的擺臂低階振動(dòng)頻率問題[5]；上官文斌,蔣翠翠等研究了含有球鉸和襯套的汽車懸架控制臂優(yōu)化設(shè)計(jì)模型，利用拓?fù)鋬?yōu)化技術(shù)對(duì)懸架控制臂進(jìn)行了優(yōu)，根據(jù)優(yōu)化結(jié)果重新設(shè)計(jì)了懸架的控制臂并對(duì)其進(jìn)行了應(yīng)力、剛度和固有頻率的計(jì)算[6]；Dong-Chan Lee 和 Jeong-Ick Lee[7]對(duì)鋁合金擺臂進(jìn)行了拓?fù)鋬?yōu)化和有限元分析，提出了新型鋁合金擺臂的輕量化設(shè)計(jì)結(jié)構(gòu)，并實(shí)現(xiàn)了制造和應(yīng)用；B-C Song，Y-C Park[8]等人對(duì)某車的懸架上擺臂利用結(jié)構(gòu)優(yōu)化技術(shù)和Kriging插值優(yōu)化理論進(jìn)行了擺臂結(jié)構(gòu)的輕量化設(shè)計(jì)。

1 基于密度法的拓?fù)鋬?yōu)化理論

1.1 密度法拓?fù)鋬?yōu)化設(shè)計(jì)變量

拓?fù)鋬?yōu)化是結(jié)構(gòu)優(yōu)化方法中的一種，本文采用基于連續(xù)體的變密度法拓?fù)鋬?yōu)化理論，建立單元密度和材料屬性之間的關(guān)系。

基于變密度法思想，材料的剛度屬性被假定的認(rèn)為與密度成線性關(guān)系，其方程表達(dá)式如下所示。每個(gè)單元的楊氏模量Ei可以用方程式（2）來(lái)表示。

式中，ρi是第i個(gè)單元的材料密度；ρ0初始的材料密度；xi為相對(duì)密度；Ei為第i個(gè)單元楊氏模量；E0為原始的楊氏模量；n為懲罰因子。其中相對(duì)密度xi就是拓?fù)鋬?yōu)化密度法的設(shè)計(jì)變量。

1.2 設(shè)計(jì)變量與材料屬性的關(guān)系

相對(duì)密度是拓?fù)鋬?yōu)化密度法的設(shè)計(jì)變量，它由空間的微結(jié)構(gòu)（單胞）確定，單胞結(jié)構(gòu)的增刪決定了相對(duì)密度值的大小，即在密度區(qū)間[0，1]之間存在著中間密度單元。每個(gè)微結(jié)構(gòu)的設(shè)計(jì)變量則是空間矩形的寬度、深度以及方向，由此來(lái)定義材料的密度和彈性[9]。平面單元和實(shí)體單元相對(duì)密度與空間尺寸的關(guān)系和表示方法如圖1所示。

圖1 相對(duì)密度微結(jié)構(gòu)單元

平面單元的相對(duì)密度為：

式中(1-a)(1-b)代表的是一個(gè)單元所占的空間面積。當(dāng)a=b=0，表示單元為空，即xi=0；當(dāng)a=1或b=1時(shí)，則表示該單元為實(shí)，即相對(duì)密度xi=1。

實(shí)體單元的相對(duì)密度為：

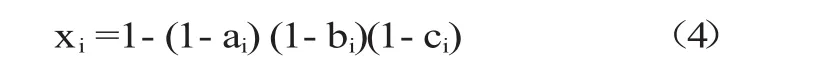
由應(yīng)力—應(yīng)變關(guān)系，{б}=[D]{ε}，式中彈性系數(shù)與相對(duì)密度的關(guān)系如方程（5）～（7）所示。

各向同性材料的平面應(yīng)力應(yīng)變的彈性系數(shù)[D]與相對(duì)密度的關(guān)系矩陣為：

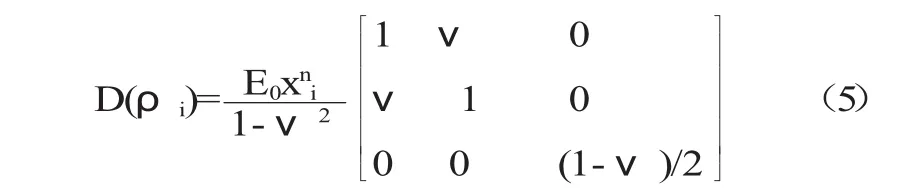
將式（3）代入式（5）中可得彈性系數(shù)矩陣與空間單元尺寸參數(shù)之間關(guān)系為：

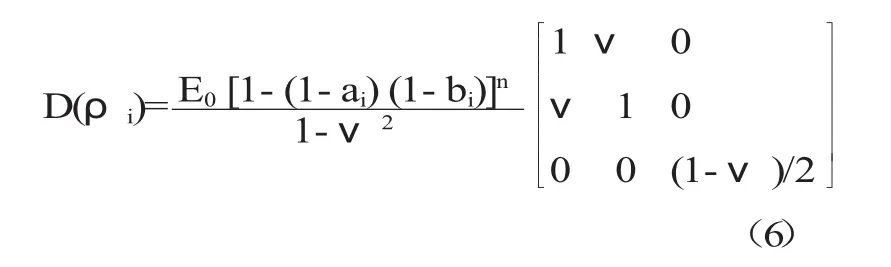
同理，各向同性材料的實(shí)體單元的彈性系數(shù)[D]與結(jié)構(gòu)設(shè)計(jì)變量相對(duì)密度之間的關(guān)系矩陣為：

1.3 設(shè)計(jì)變量與結(jié)構(gòu)的單元?jiǎng)偠汝P(guān)系

在有限元靜力學(xué)求解時(shí)，當(dāng)結(jié)構(gòu)的變形在材料彈性范圍以內(nèi)時(shí)，結(jié)構(gòu)剛度和位移之間的關(guān)系則滿足廣義的胡克定律，其方程為：

因此結(jié)構(gòu)的單元?jiǎng)偠染仃嘯K]與設(shè)計(jì)變量之間的關(guān)系可以表示為：

式中：[B]矩陣為常系數(shù)矩陣。

2 懸架擺臂的工況分析

汽車懸架擺臂相對(duì)于整個(gè)車體結(jié)構(gòu)的布置和設(shè)計(jì)來(lái)說是很小的一個(gè)部分，但是它卻傳遞著來(lái)自路面的一切力和力矩，因此汽車懸架擺臂的工況分析是設(shè)計(jì)擺臂結(jié)構(gòu)的一個(gè)重要環(huán)節(jié)。

汽車懸架下擺臂最典型的三種極限工況為：

（1）垂直沖擊工況；路面對(duì)車輪的垂直沖擊力通過轉(zhuǎn)向節(jié)、球頭銷、擺臂和螺旋彈簧傳到車架和車身上，此時(shí)車輪所受的垂直力最大，縱向力和側(cè)向力相對(duì)較小，其影響忽略，在整車坐標(biāo)系下車輪的縱向力FX=0，側(cè)向力 FY=0。

（2）轉(zhuǎn)彎工況；作用在車輪上的側(cè)向力矩及其力矩由轉(zhuǎn)向節(jié)及其導(dǎo)向機(jī)構(gòu)經(jīng)過懸架傳遞到車架上，考慮急轉(zhuǎn)彎的極限情況，此時(shí)縱向力相對(duì)于側(cè)向力較小，可以忽略，因此有車輪的縱向力FX=0。

（3）制動(dòng)工況；制動(dòng)工況時(shí)，輪胎的縱向力達(dá)到最大，此時(shí)側(cè)向力較小可以忽略，則有FY=0。

根據(jù)某越野車懸架下擺臂的結(jié)構(gòu)尺寸和在整車中的布置位置關(guān)系，這三種工況下該越野車懸架下擺臂的載荷大小如表1所示，表1中的數(shù)據(jù)是已經(jīng)換算到了擺臂坐標(biāo)系下的載荷關(guān)系。

表1 三種工況的載荷情況

3 多工況懸架擺臂拓?fù)鋬?yōu)化數(shù)學(xué)模型

3.1 多工況結(jié)構(gòu)優(yōu)化的定義

本文設(shè)計(jì)的越野車懸架下橫臂主要應(yīng)用的工況有極限垂直沖擊、轉(zhuǎn)彎、剎車三種，在對(duì)鍛鋁合金材料對(duì)下橫臂進(jìn)行概念設(shè)計(jì)階段的拓?fù)鋬?yōu)化時(shí)，如果采用單工況拓?fù)鋬?yōu)化方法，所使用的工程分析時(shí)間比較長(zhǎng)，有可能需要幾輪的優(yōu)化和幾何重構(gòu)過程。這不僅僅加大了設(shè)計(jì)的時(shí)間成本，而且所設(shè)計(jì)出的結(jié)構(gòu)不一定是最優(yōu)的、滿足各工況性能要求的結(jié)構(gòu)。基于此本文提出了基于加權(quán)應(yīng)變能的拓?fù)鋬?yōu)化方法來(lái)處理在拓?fù)鋬?yōu)化階段的多工況問題。

在Optistruct結(jié)構(gòu)優(yōu)化設(shè)計(jì)中，加權(quán)應(yīng)變能響應(yīng)的定義為每個(gè)子工況應(yīng)變能的加權(quán)和，其表達(dá)式為：

式中，Cj為第j個(gè)工況的應(yīng)變能；ωj為該工況的加權(quán)系數(shù)，其取值范圍在0.1～1.0之間；uTi為位移矩陣的轉(zhuǎn)置。

通過加權(quán)應(yīng)變能的加權(quán)和定義了每個(gè)子工況在擺臂結(jié)構(gòu)拓?fù)鋬?yōu)化下的權(quán)重，該權(quán)重根據(jù)擺臂在汽車懸架工作中的真實(shí)情況來(lái)評(píng)定，這樣結(jié)構(gòu)優(yōu)化設(shè)計(jì)的結(jié)果將會(huì)更加的接近實(shí)際情況。

3.2 拓?fù)鋬?yōu)化數(shù)學(xué)模型

基于加權(quán)應(yīng)變能的拓?fù)鋬?yōu)化方法，該方法以極限垂直沖擊、轉(zhuǎn)彎、剎車三種工況的加權(quán)應(yīng)變能最小為目標(biāo)函數(shù)，以設(shè)計(jì)區(qū)域的體積分?jǐn)?shù)為約束，以設(shè)計(jì)區(qū)域的材料密度為設(shè)計(jì)變量。

在結(jié)構(gòu)的拓?fù)鋬?yōu)化過程中，把剛度最大問題等效為柔度最小問題來(lái)研究，柔度則用應(yīng)變能來(lái)定義。因此，該問題的優(yōu)化目標(biāo)可以轉(zhuǎn)化為全局柔度最小問題。采用Optistruct模型常用的多剛度線性疊加的模型將多個(gè)工況下的柔度目標(biāo)值綜合表述為全局柔度目標(biāo)值，因此拓?fù)鋬?yōu)化的數(shù)學(xué)模型為：

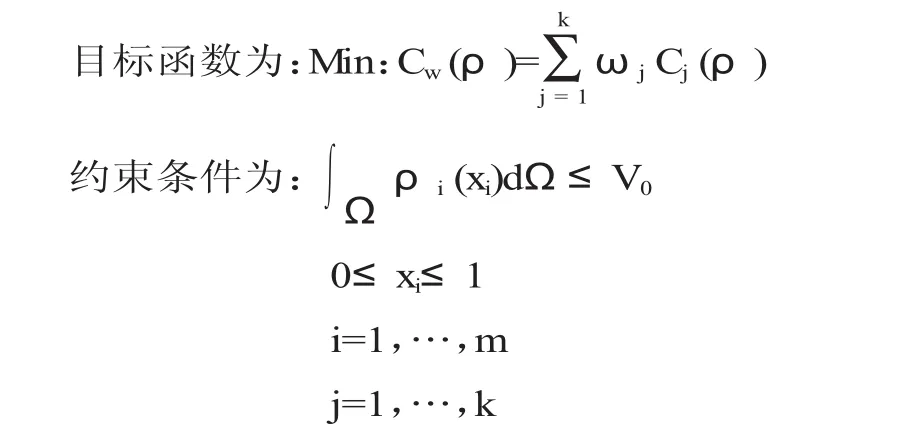
式中，Ω為拓?fù)湓O(shè)計(jì)區(qū)域；V0為結(jié)構(gòu)初始體積。

因此，某越野車鍛鋁合金下擺臂多工況下的拓?fù)鋬?yōu)化問題的描述如下：

優(yōu)化區(qū)域：如圖2所指示的區(qū)域；

目標(biāo)函數(shù)：懸架下橫臂的整體剛度最大，即加權(quán)應(yīng)變能最小；

約束條件：懸架下橫臂的體積分?jǐn)?shù)大于0.4小于0.6；

設(shè)計(jì)變量：?jiǎn)卧拿芏戎担?/p>

制造工藝約束：脫模約束；

最大應(yīng)力參數(shù)約束：小于355MPa。

圖2 擺臂結(jié)構(gòu)拓?fù)鋷缀文Ｐ?/p>

4 結(jié)果和分析

4.1 擺臂結(jié)構(gòu)的拓?fù)鋬?yōu)化結(jié)果

結(jié)構(gòu)拓?fù)鋬?yōu)化設(shè)計(jì)采用商用軟件Hyperworks中的Optistruct優(yōu)化設(shè)計(jì)模塊完成。經(jīng)過18次迭代，結(jié)構(gòu)優(yōu)化計(jì)算收斂，將計(jì)算結(jié)構(gòu)文件導(dǎo)進(jìn)hyperview軟件后，查看優(yōu)化后的模型。圖3是優(yōu)化計(jì)算的迭代過程圖，圖4是單元去年密度值大于0.3的密度云圖。

圖3 拓?fù)涞鷪D

圖4 擺臂密度云圖

根據(jù)結(jié)構(gòu)拓?fù)浜蟮拿芏仍茍D，取材料密度值大于0.3的部分對(duì)懸架下擺臂的結(jié)構(gòu)進(jìn)行三維建模并獲得了鍛鋁合金下擺臂結(jié)構(gòu)，懸架下擺臂的CAD模型圖如圖5所示。

圖5 鍛鋁合金下擺臂結(jié)構(gòu)

4.2 擺臂結(jié)構(gòu)有限元分析結(jié)果

為了將拓?fù)鋬?yōu)化后的鋁合金擺臂結(jié)構(gòu)與鑄鋼材料的結(jié)構(gòu)性能進(jìn)行對(duì)比，本文采用有限元分析方法分別對(duì)兩種材料的結(jié)構(gòu)進(jìn)行了三種工況下強(qiáng)度和剛度分析。有限元分析的結(jié)果如表所示。

（1）鑄鋼材料下擺臂的有限元分析結(jié)果

三種工況下最大應(yīng)力和最大位移值如表2所示。

表2 鍛鋼下擺臂有限元分析結(jié)果

（2）鋁合金材料下擺臂的有限元分析結(jié)果

鋁合金拓?fù)鋬?yōu)化下擺臂結(jié)構(gòu)在三種工況下的最大應(yīng)力和位移值如表3所示。

表3 鋁合金下擺臂有限元分析結(jié)果

（3）結(jié)果分析

根據(jù)有限元分析的結(jié)果，為了驗(yàn)證和評(píng)價(jià)拓?fù)浣Y(jié)構(gòu)的性能，將對(duì)鑄鋼擺臂和鋁合金擺臂從強(qiáng)度、剛度和結(jié)構(gòu)重量三個(gè)方面進(jìn)行對(duì)比分析。擺臂結(jié)構(gòu)性能對(duì)比如表5所示。

表4 鑄鋼材料與鍛鋁材料下橫臂性能對(duì)比

1）強(qiáng)度分析

由表5可知，兩種不同材料的強(qiáng)度對(duì)比：鋁合金材料下橫臂的最大應(yīng)力為277 MPa，鑄鋼材料下橫臂的最大應(yīng)力為910 MPa，都小于各自材料的屈服極限，滿足項(xiàng)目中所提出的設(shè)計(jì)要求。

2）剛度分析

由以上兩種材料下橫臂的剛度分析可知：鋁合金的下橫臂在垂直沖擊工況的最大位移比鑄鋼材料的小了0.17mm，轉(zhuǎn)彎工況小了0.26mm，剎車工況小了0.34mm，鍛鋁材料下橫臂結(jié)構(gòu)剛度比鍛鋼材料結(jié)構(gòu)在三種工況下都有提高和改進(jìn)。

3）結(jié)構(gòu)重量對(duì)比

由表5對(duì)兩種不同材料的下橫臂的質(zhì)量對(duì)比可知，鍛鋁材料下橫臂的重量為11.04 Kg，比鑄鋼材料的下橫臂減小了1.52 Kg，由于該越野車前后懸架都采用雙橫臂式獨(dú)立懸架，這樣，該越野車如果采用鋁合金材料制造下橫臂的話，那么在下橫臂上可以減重1.52X4=6.08Kg，相對(duì)于鑄鋼材料下橫臂，鋁合金材料減重約12.10%。

5 結(jié)論

通過有限元分析以及與鑄鋼材料擺臂結(jié)構(gòu)性能對(duì)比可以證明，拓?fù)鋬?yōu)化可以減輕擺臂質(zhì)量，同時(shí)改善擺臂的剛、強(qiáng)度特性，對(duì)于汽車輕量化設(shè)計(jì)有著重大意義。

[1]謝文林.車用塑性零部件生產(chǎn)情況及2000年市場(chǎng)需求預(yù)測(cè)[J].汽車世界,1997,(2)：29～31.

[2]桑楠,白玉等.基于ABAQUS的汽車前擺臂輕量化設(shè)計(jì)[J].長(zhǎng)春工程學(xué)院學(xué)報(bào),2010,(11)2.

[3]王鳳軍,扶原放等.基于可靠性原理的懸架下擺臂輕量化設(shè)計(jì)研究[J].汽車工程,2009,(31)11.

[4]張兆良.雙橫臂懸架上、下擺臂輕量化設(shè)計(jì)[J].北京汽車,2010,2.

[5]祝小元,方宗德等.汽車懸架控制臂的多目標(biāo)拓?fù)鋬?yōu)化[J].汽車工程,2011,(33)2.

[6]上官文斌,蔣翠翠等.汽車懸架控制臂的拓?fù)鋬?yōu)化與性能計(jì)算[J].汽車工程,2008,(30)8.

[7]Dong-Chan Lee,Jeong-Ick Lee.Structural optimization concept for the design of an aluminum control arm[J].Automobile Engineering,2003,Vol.217.

[8]B-C Song,Y-C Park,S-W Kang,K-H Lee.Structural optimization of an upper control arm,considering the strength[J].Automobile Engineering,2009,Vol.223.

[9]張勝蘭等.基于Hyperworks的結(jié)構(gòu)優(yōu)化設(shè)計(jì)技術(shù)[M].機(jī)械工業(yè)出版社,2007.