預應力引起的曲線箱梁橋支座反力與位移研究

黃 超，譚長瑞，段 鵬

(1．重慶交通大學土木建筑學院，重慶400074;2．北京中桀偉業道路工程技術有限公司，北京100101;3．重慶建筑工程職業學院，重慶400039)

1 曲繞箱梁橋的病害

隨著我國城市規模不斷增大，道路交通逐漸成為制約城市發展的主要因素之一。為了在有限的地理空間上建立起順暢的交通系統，許多城市修建了各種高架橋、互通式立交工程。曲線箱梁橋以其良好的地形適應性和對城市景觀的美化效果，成為了高架橋或者立交工程的主要結構形式。在工程實踐中，曲線梁橋也表現出了各種病害，參考國內外已出現的曲線梁橋事故，可總結為如下四種常見病害。

1.1 梁體向外側移和翻轉

由于“彎－扭耦合”效應，曲線梁在荷載作用下繞某一軸線旋轉，產生水平面和豎平面位移，例如深圳市華強立交A匝道第三聯在投入使用兩年后，曲線梁橋突然向外移動和向外側翻轉，曲線梁體徑向最大位移為47 cm，切向最大位移為16 cm。

1.2 固結墩墩身開裂

對于某些曲率半徑較小的連續曲線梁橋，在設計中為了控制跨中梁體的側向變形，將中間墩設置為墩梁固結墩，或者在中間墩處設置側向限位裝置。在預應力、溫度、汽車離心力等荷載的作用下，中間墩支座承受較大的水平反力，墩身出現水平裂縫，當這種水平力較大時，甚至造成中間墩破壞。

1.3 腹板內預應力筋崩出

預應力混凝土曲線箱梁橋在張拉縱向力筋時，預應力鋼束產生的徑向水平壓力易使箱梁腹板超載，嚴重時造成腹板混凝土崩裂破壞，預應力鋼束繃直并從腹板內崩出。

1.4 內側支座脫空

曲線梁橋在豎向荷載作用下，內側、外側支座支反力相差較大，當汽車荷載偏載時，這種差異可能導致外側支座超出承載能力極限而內側支座承載能力尚未充分發揮的情況(偏載效應較大時內側支座甚至出現拉力)，即內側支座脫空。

2 曲線梁橋的受力特性

由于存在平面曲率半徑，同直線梁橋相比，曲線箱梁橋有著獨特的受力特性。在自重、活載、預應力荷載以及溫度荷載作用下，曲線梁橋產生彎矩的同時，伴隨產生扭矩，反之，在產生扭矩時也會產生彎矩，即“彎－扭耦合”效應［1］;在移動荷載作用下(移動的汽車荷載)，曲線梁橋承受曲率平面內的離心力荷載。在結構變形方面，曲線梁橋在荷載作用下會產生水平面位移和豎平面位移，變形呈三維空間特性。預應力混凝土曲線箱梁橋中，預應力鋼束線形為空間曲線，在預應力作用下，梁體為空間受力體系，其內力和變形分析十分復雜，本文擬采用數值分析方法，以重慶市某小區一座小半徑曲線箱梁橋為背景，運用通用有限元軟件ANSYS分析預應力引起的該橋內外側支座反力差值與位移情況。

3 ANSYS 模擬預應力結構的基本原理［3］

ANSYS作為一款較成熟的大型通用有限元軟件，近年來被越來越多的應用于土建工程領域，同模型試驗相比，用ANSYS進行數值模擬可以顯著的降低成本，而且能夠模擬各種復雜的邊界條件。ANSYS模擬預應力效應主要有兩種方式:(1)等效荷載法:用一組“等效荷載”替代預應力筋的作用施加到結構上，該方法的優點是:建模簡單，不必考慮力筋的具體位置，單元劃分較靈活，其主要缺點是無法模擬張拉過程中引起的預應力損失，局部計算結果同實際情況相差較大;(2)實體力筋法:預應力筋和混凝土獨立建模，力筋多采用LINK系列單元，混凝土采用SOLID系列實體單元，通過兩種單元的節點耦合或者建立約束方程來模擬預應力效應，該方法可有效消除等效荷載法的缺點，可對預應力混凝土結構的應力分析進行精確模擬，但是該方法建模復雜，對計算機的系統配置要求高，且可能出現求解不收斂的情況，故該方法一般用于重要結構的局部分析，本文算例中，計算模型采用第二種方法建模，預應力效應通過初應變施加到結構上。

4 計算模型說明

本文算例中，橋軸線(箱梁中心線，不考慮橫橋向坡度)半徑R=45m，跨徑30m，采用單箱雙室截面，箱梁橫截面尺寸詳見圖1。

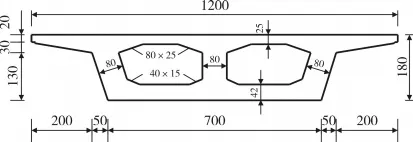
圖1 箱梁橫截面

箱梁混凝土為C50，混凝土應力－應變關系采用《混凝土結構設計規范》(GB 50010－2002)中規定的曲線，即由拋物線上升段和水平線組成［2］，上升段的數學表達式為:σc=fc［1－(1－εc/ε0)2］，式中:fc為混凝土抗壓強度設計值，文中取 fc=32.4 MPa，ε0=0.002。混凝土應力－應變關系曲線如圖2所示。

圖2 混凝土應力－應變關系

箱梁內預應力鋼束規格為:15Φs15.2，內、中、外腹板各布置6束，鋼束標準強度fpk=1 860 MPa，彈性模量:Ep=1.95×105MPa，錨下張拉控制應力:σcon=0.70 fpk=1 302 MPa。

文中預應力通過初應變施加于箱梁上，為簡化建模，將內、中、外腹板的預應力鋼束等效為三束，每束的初應變為:ε=σ/E=6.677×10－3，截面積為:A=15×139×10－6×6=1.251×10－2m2。鋼束采用LINK8單元，混凝土采用SOLI65單元，鋼束與混凝土之間的作用通過節點自由度耦合進行模擬，橋梁采用抗扭支座，0號墩為固結支座，1號墩為豎向、徑向約束支座，模型求解時考慮材料非線性影響［4］，全橋SOLID65單元共4 440個，LINK8單元共368個，全橋模型單元離散圖如圖3所示。

圖3 模型單元離散圖

5 數值分析結果及評價

5.1 內側、外側支座支反力分析

為了清楚反映預應力對支座支反力的影響程度，計算模型考慮兩種工況，工況一:曲線箱梁僅承受預應力荷載;工況二:曲線箱梁承受預應力荷載與自重荷載。進行有限元模型求解，根據通用后處理器(post1)列出0號墩、1號墩內外側支座在兩種工況下的支反力如下表所示，表1為工況一下各支座反力，表2為工況二下各支座反力。表中豎向力方向以向上為正。

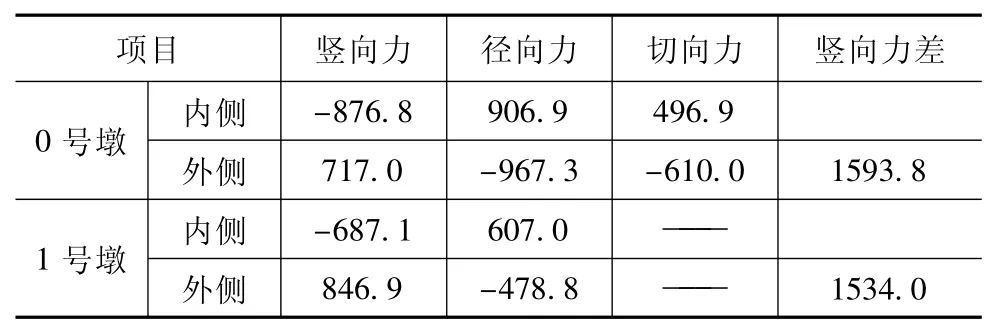
表1 預應力作用下的支反力(kN)

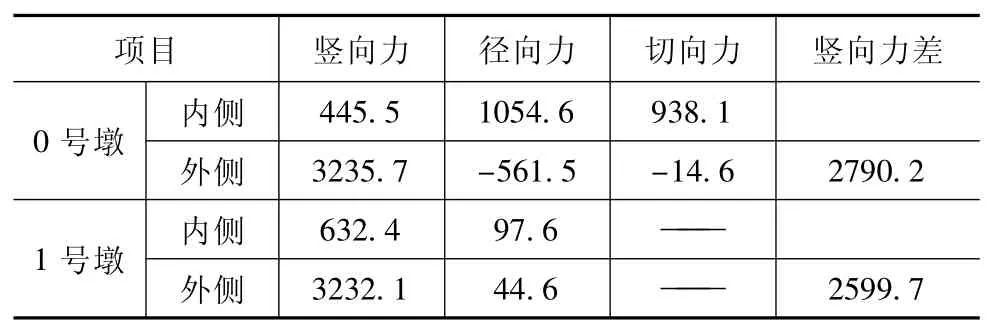
表2 預應力與自重共同作用下的支反力(kN)

通過上述兩個表格可以看出:在預應力荷載單獨作用下，曲線箱梁的外側支座支反力值較大，內側支反力為負，即支座處出現拉力(這與實際情況不符，其原因為在模型中支座處設置為豎向雙向約束);在自重和預應力荷載共同作用下，內側、外側支座反力均向上，對比兩種工況:預應力引起的豎向力差占總差值百分比為:η=1534/2599.7=59%，說明在恒荷載(模型中未考慮二期恒載和欄桿等附屬設施的自重)作用下，預應力引起的內外側支反力差值占總差值的主要部分。從表1和表2還可以看出，在預應力作用下，曲線箱梁橋支座處產生徑向反力和切向反力，其中徑向力遠大于切向力，表明預應力引起的曲梁繃直的趨勢較曲梁軸線壓縮要強。

5.2 預應力荷載作用下曲線箱梁頂平面內緣、外緣位移分析

根據數值分析結果，繪制預應力荷載作用下曲線箱梁頂板內緣、外緣的豎向位移(u－z)、水平面內位移(u－xy)以及總位移向量(u－sum)圖如圖4、圖5。

由圖4、圖5可以看出，在預應力作用下，曲線箱梁出現向上撓曲變形，外緣最大變形(豎向位移u－z)為9mm，內緣最大變形為13mm，梁體呈向外側翻轉趨勢;曲線箱梁的變形以豎平面變形為主，外緣水平面位移叫內緣大，表明箱梁在預應力荷載作用下，橫截面發生了畸變變形。

圖4 外緣豎向位移

圖5 內緣豎向位移

5.3 預應力與自重荷載作用下曲線箱梁頂平面內緣、外緣位移分析［5］

根據模型計算結果，繪制曲線箱梁在預應力與自重荷載共同作用下的位移如圖6、圖7所示。

圖6 外緣豎向位移

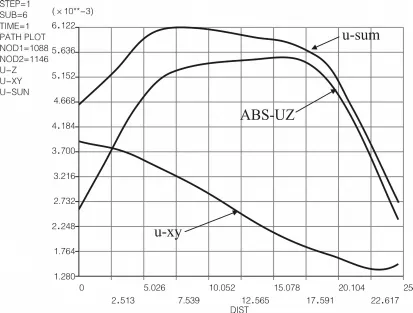
圖7 內緣豎向位移

從上圖可以看出，在預應力和自重荷載共同作用下，曲線箱梁產生了水平面位移與豎平面位移，箱梁頂板內緣、外緣變形差值較小，對比5.2節中結論，可以看出自重荷載緩和了預應力荷載引起的箱梁翻轉趨勢。

5.4 結論及建議

(1)小半徑曲線箱梁橋在預應力荷載作用下，內外側支座均產生支反力，內側為拉、外側為壓，且支反力差值為恒載產生支反力差值的主要部分;在水平面內，支座處產生徑向約束和切向約束(徑向、切向均約束的支座)。

(2)曲線箱梁橋在預應力作用下，梁體產生豎向和水平變形，其中豎向變形占主導部分，整個箱梁呈現向外側翻轉的趨勢，自重荷載可在一定程度上消減箱梁內側、外側的豎向位移差值［6］。

(3)設有雙支座曲線箱梁橋，外側支座承受的豎向荷載較內側支座大，設計時應考慮內、外側支座采用不同型號，或者增大支座承載力儲備值，以防止外側支座已經被壓壞而內側支座的承載力尚未充分受力的情況［7］。

［1］ 姚玲森．曲線梁［M］．北京:人民交通出版社，1987:7－12

［2］ 江見鯨．鋼筋混凝土結構非線性有限元分析［M］．西安:陜西科學技術出版社，1993

［3］ 王新敏．ANSYS工程結構數值分析［M］．北京:人民交通出版社，1993

［4］ 趙穎華，李秀文，徐進．兩端簡支超靜定曲線梁橫向位移解析分析［J］．沈陽建筑大學學報，2005，21(3):189－191

［5］ 程進，沈旭東．基于ANSYS預應力混凝土曲線梁橋三維施工仿真分析［J］．公路交通科技，2007，24(4):108－112

［6］ 金菊，王淑濤．中小跨徑曲線梁橋半徑變化對結構變形的影響分析［J］．河北工業大學學報，2007，36(4):110－113

［7］ 張蕊．曲線梁橋設計分析［J］．公路工程與運輸，2008，8(4):128－130